Carrier Frequency Systems with Coherent Demodulation

1 Signal space representation of linear modulation
2 Coherent demodulation and optimal receiver
3 On–off keying (2–ASK)
4 Binary phase shift keying (BPSK)
5 M–level amplitude shift keying (M–ASK)
6 Quadrature amplitude modulation (M-QAM)
7 Multi-level phase–shift keying (M–PSK)
8 Binary frequency shift keying (2–FSK)
9 Minimum Shift Keying (MSK)
10 Aufgaben zum Kapitel
11 Quellenverzeichnis

Signal space representation of linear modulation

In the first three chapters of this "fourth main chapter" "Generalized Description of Digital Modulation Methods" the structure of the optimal receiver and the signal representation by means of basis functions were treated by the example of baseband transmission.

With the same systematics and the same uniformity, band–pass systems will now also be considered which have already been described in earlier books or chapters, namely

in the main chapter 4: "Digital Modulation Methods" of the book "Modulation Methods",

in the chapter "Linear Digital Modulation - Coherent Demodulation" of the present book.

In the following, we restrict ourselves to linear modulation methods and coherent demodulation. This means that the receiver must know exactly the frequency and phase of the carrier signal added to the transmitter. In the following chapter, "Carrier Frequency Systems with Non-Coherent Demodulation" are discussed.

In the case of coherent demodulation, the entire transmission system can be described in the "equivalent low-pass domain", and the relationship to baseband transmission is even more obvious than when band-pass signals are considered.

Equivalent low-pass model of carrier-modulated transmission methods

This results in the sketched model. Complex quantities are marked by a yellow filled double arrow. It should be noted with regard to this graph:

From the incoming bit stream $\langle q_k \rangle \in \{\rm 0, \ L \}$, $b$ data bits each are converted serially/parallel. These output bits result in the message $m \in \{m_0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, m_{M-1} \}$, where $M = 2^b$ indicates the level number. For the following, the message $m = m_i$ is assumed.

In the signal space allocation, a complex amplitude coefficient $a_i = a_{{\rm I}i} + {\rm j} \cdot a_{{\rm Q}i}$ is assigned to each message $m_i$, whose real part will form the in-phase component and whose imaginary part will form the quadrature component of the later transmitted signal.

At the output of the blue marked block generation of the TP signal the (in general) complex-valued "equivalent low-pass signal" is present, where $g_s(t)$ shall be limited for the time being to the range $ 0 \le t \le T$ just like $s_{\rm TP}(t)$. The index $i$ again provides an indication of the message $m_i$ sent:

\[s_{\rm TP}(t) \big {|}_{m \hspace{0.05cm}= \hspace{0.05cm} m_i} = a_i \cdot g_s(t) = a_{{\rm I}i} \cdot g_s(t) + {\rm j} \cdot a_{{\rm Q}i} \cdot g_s(t)\]

By energy normalization one gets from the basic transmission pulse $g_s(t)$ to the basis function

\[\varphi_1(t) = { g_s(t)}/{\sqrt{E_{gs}}} \hspace{0.4cm} {\rm with} \hspace{0.4cm} E_{gs} = \int_{0}^{T} g_s(t)^2 \,{\rm d} t \hspace{0.3cm} \Rightarrow \hspace{0.3cm} s_{\rm TP}(t) \big {|}_{m\hspace{0.05cm} =\hspace{0.05cm} m_i} = s_{{\rm I}i} \cdot \varphi_1(t) + s_{{\rm Q}i} \cdot {\rm j} \cdot \varphi_1(t) \hspace{0.05cm}.\]

While the coefficients $a_{{\rm I}i}$ and $a_{{\rm Q}i}$ are dimensionless, the new coefficients $s_{{\rm I}i}$ and $s_{{\rm Q}i}$ have the unit "root of energy" ⇒ see page "Nomenclature in the fourth chapter":

\[s_{{\rm I}i} = {\sqrt{E_{gs}}} \cdot a_{{\rm I}i}\hspace{0.05cm}, \hspace{0.2cm} s_{{\rm Q}i} = {\sqrt{E_{gs}}} \cdot a_{{\rm Q}i}\hspace{0.05cm}. \]

The equations show that the system considered here is completely described in the equivalent TP domain by one real basis function $\varphi_1(t)$ and one purely imaginary basis function $\psi_1(t) = {\rm j} \cdot \varphi_1(t)$ each, or by a single complex basis function $\xi_1(t)$.

The gray shaded part of the block diagram shows the model for generating the band-pass signal $s_{\rm BP}(t)$, first the generation of the "analytical signal" $s_{\rm +}(t) = s_{\rm TP}(t) \cdot {\rm e}^{{\rm j}2\pi \cdot f_{\rm T} \cdot T}$ and then the real part formation.

The two basis functions of the band-pass signal $s_{\rm BP}(t)$ result here as energy-normalized and time-limited to the range $0 \le t \le T$ cosine and minus-sine oscillations, respectively.

Coherent demodulation and optimal receiver

In the following, we always assume the equivalent low-pass signal unless explicitly stated otherwise. In particular, the signals $s(t) = s_{\rm TP}(t)$ and $r(t) = r_{\rm TP}(t)$ in the graph are low-pass signals and thus generally complex. The suffix "TP" is omitted in the remainder of this paper.

AWGN channel model for complex signals

To this figure is to be noted:

The phase delay of the channel (i.e. a phase function increasing linearly with frequency) is expressed in the low-pass range by the time-independent rotation factor ${\rm e}^{{\rm j}\hspace{0.05cm} \phi}$.

The signal $n\hspace{0.05cm}'(t)$ describes a complex white Gaussian random process in the TP domain, as given in the section "N-dimensional Gaussian noise". The apostrophe was added in order to be able to work with $n(t)$ later in the overall system.

The receiver knows the channel phase $\phi$ and corrects it by the conjugate-complex rotation factor ${\rm e}^{-{\rm j}\hspace{0.05cm}\phi}$. Thus the received signal in the equivalent low-pass range is:

\[r(t) = s(t) + n\hspace{0.05cm}'(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\phi}= s(t) + n(t) \hspace{0.05cm}.\]

The phase rotation does not change the properties of the circular symmetric noise ⇒ $n(t) = n\hspace{0.05cm}'(t) \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\phi}$ has exactly the same statistical properties as $n\hspace{0.05cm}'(t)$.

The left graphic in the figure above illustrates the facts just described.

The right graph shows the overall system as used for the rest of the fourth main chapter.
The AWGN channel is followed by an optimal receiver according to the section "N-dimensional Gaussian noise".

$\text{Definition:}$ A symbol error occurs whenever $\hat{m}$ does not match the message $m$ sent:

\[m = m_i \hspace{0.2cm} \cap \hspace{0.2cm} \hat{m} \ne m_i \hspace{0.05cm}.\]

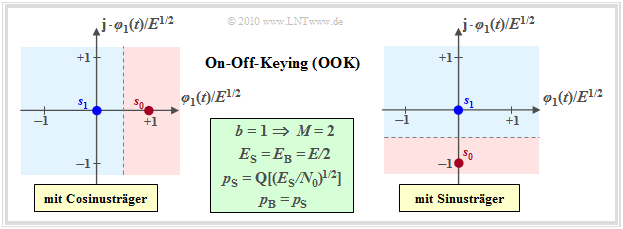
On–off keying (2–ASK)

The simplest digital modulation method is On–off keying (OOK), which has already been described in detail in the book "Modulation Methods" on the basis of its band-pass signals. There this method was partly also called Amplitude Shift Keying (2–ASK).

Signal space constellations for on-off keying

This method can be characterized as follows:

OOK is a one-dimensional modulation method $(N = 1)$ with $s_{{\rm I}i} = \{0, E^{1/2}\}$ and $s_{{\rm Q}i} \equiv 0$ or $s_{{\rm I}i} \equiv 0$ and $s_{{\rm Q}i} = \{0, -E^{1/2}\}$. As an abbreviation, $E = E_{g_s}$. The first combination describes a cosinusoidal carrier signal, the second combination a sinusoidal carrier.

Each bit is assigned to a binary symbol $(b = 1, \ M = 2)$; thus, no serial/parallel converter is needed. For equally probable symbols, which is always assumed for what follows, both the mean energy per symbol $(E_{\rm S})$ and the mean energy per bit $(E_{\rm B})$ are equal to $E/2$.

The optimal OOK receiver virtually projects the complex-valued received signal $r(t)$ onto the basis function $\varphi_1(t)$, if one starts from the left sketch (cosine carrier).

Because of $N = 1$, the noise can be one-dimensional with the variance $\sigma_n^2 = N_0/2$. Using the statements in the section "Error probability for symbols with equal probability", we obtain for the mean symbol error probability:

\[p_{\rm S} = {\rm Pr}({\cal{E}}) = {\rm Q} \left ( \frac{d/2}{\sigma_n}\right ) = {\rm Q} \left ( \sqrt{\frac{E}{2 N_0}}\right ) = {\rm Q} \left ( \sqrt{{E_{\rm S}}/{N_0}}\right ) \hspace{0.05cm}.\]

Since each bit is mapped to exactly one symbol, the average bit error probability $p_{\rm B}$ is exactly:

\[p_{\rm B} = {\rm Q} \left ( \sqrt{{E_{\rm S}}/{N_0}}\right ) = {\rm Q} \left ( \sqrt{{E_{\rm B}}/{N_0}}\right ) \hspace{0.05cm}.\]

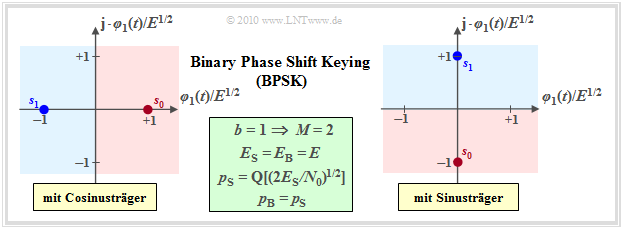
Binary phase shift keying (BPSK)

Das sehr oft angewandte Verfahren Binary Phase Shift Keying (BPSK), das bereits im Kapitel Lineare digitale Modulationsverfahren des Buches "Modulationsverfahren" anhand der Bandpass–Signale ausführlich beschrieben wurde (typisch: Phasensprünge), unterscheidet sich von On–Off–Keying durch eine konstante Hüllkurve.

Für die Signalraumpunkte gilt stets $\boldsymbol{s}_1 = -\boldsymbol{s}_0$. Sie lauten beispielsweise:

$s_{{\rm I}i} = \{\pm E^{1/2}\}$ und $s_{{\rm Q}i} \equiv 0$ bei cosinusförmigem Träger,
$s_{{\rm I}i} \equiv 0$ und $s_{{\rm Q}i} = \{\pm E^{1/2}\}$ bei sinusförmigem Träger.

Signalraumkonstellationen der BPSK

Anhand der in der Grafik angegebenen Gleichungen (im grün hinterlegten Feld) erkennt man die Verbesserungen gegenüber On–Off–Keying:

Bei gegebener Normierungsenergie $E$ ist der Abstand zwischen $\boldsymbol{s}_0$ und $\boldsymbol{s}_1$ doppelt so groß. Damit erhält man für die Fehlerwahrscheinlichkeit (sowohl bezogen auf Symbole wie auch auf Bits):

\[p_{\rm S} = p_{\rm B} = {\rm Pr}({\cal{E}}) = {\rm Q} \left ( \frac{d/2}{\sigma_n}\right ) = {\rm Q} \left ( \sqrt{{2 E}/{N_0}}\right ) = {\rm Q} \left ( \sqrt{{2 E_{\rm S}}/{N_0}}\right ) \hspace{0.05cm}.\]

In dieser Gleichung ist ebenfalls berücksichtigt, dass nun $E_{\rm S} = E_{\rm B} = E$ gilt, das heißt, dass nun die mittleren Energien pro Symbol bzw. pro Bit doppelt so groß sind als bei OOK.

Die BPSK–Fehlerwahrscheinlichkeit ist durch den Faktor $2$ unter der Wurzel im Argument der Q–Funktion merklich geringer als bei On–Off–Keying, wenn $E_{\rm S}$ und $N_0$ nicht verändert werden.

Anders ausgedrückt: BPSK benötigt bei gleichem $N_0$ nur die halbe Symbolenergie $E_{\rm S}$, um die gleiche Fehlerwahrscheinlichkeit wie On–Off–Keying zu erzielen. Der logarithmische Gewinn beträgt $3 \ \rm dB$.

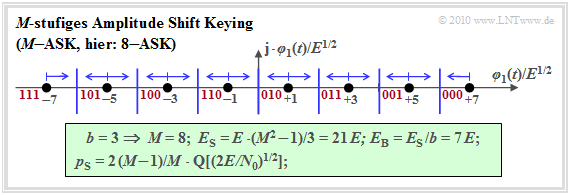
M–level amplitude shift keying (M–ASK)

In Analogie zur M–stufigen Basisbandübertragung betrachten wir nun ein $M$–stufiges Amplitude Shift Keying ($M$–ASK), dessen Tiefpass–Signalraumkonstellation für die Parameter $b = 3$ ⇒ $M = 8$ ⇒ $8$–ASK wie folgt aussieht.

Signalraumkonstellation der 8-ASK

Der Name $M$–ASK ist nicht ganz zutreffend. Vielmehr handelt es sich um ein kombiniertes ASK/PSK–Verfahren, da sich zum Beispiel die beiden innersten Signalraumpunkte $(\pm 1)$ nicht in der Amplitude (Hüllkurve) unterscheiden, sondern nur durch die Phase ($0^\circ$ bzw. $180^\circ$).

Weiter ist anzumerken:

Die mittlere Energie pro Symbol kann man für dieses eindimensionale Verfahren unter Ausnutzung der Symmetrie wie folgt berechnen:

\[E_{\rm S} = \frac{2}{M} \cdot \sum_{k = 1}^{M/2} (2k -1)^2 \cdot E = \frac{M^2 -1}{3} \cdot E \hspace{0.05cm}.\]

Da jedes der $M$ Symbole $b = \log_2 (M)$ Bit darstellt, erhält man für die mittlere Energie pro Bit:

\[E_{\rm B} = \frac{E_{\rm S}}{b} = \frac{E_{\rm S}}{{\rm log_2}\, (M)} =\frac{M^2 -1}{3 \cdot {\rm log_2}\, (M)} \cdot E \hspace{0.3cm}\Rightarrow\hspace{0.3cm}M= 8\hspace{-0.1cm}: E_{\rm S}/E = 21 \hspace{0.05cm}, \hspace{0.1cm}E_{\rm B}/E = 7\hspace{0.05cm}.\]

Die Wahrscheinlichkeit, dass eines der beiden äußeren Symbole aufgrund von AWGN–Rauschen verfälscht wird, ist somit gleich

\[{\rm Pr}({\cal{E}} \hspace{0.05cm}|\hspace{0.05cm} \text{äußeres Symbol)} = {\rm Q} \left ( \sqrt{{2 E}/{N_0}}\right )\hspace{0.05cm}.\]

Die Verfälschungswahrscheinlichkeit der $M-2$ inneren Symbole ist doppelt so groß, da hier sowohl rechts als auch links andere Entscheidungsregionen angrenzen. Durch Mittelung erhält man für die (mittlere) Symbolfehlerwahrscheinlichkeit:

\[p_{\rm S} = {\rm Pr}({\cal{E}}) = \frac{1}{M} \cdot \left [ 2 \cdot 1 \cdot {\rm Q} \left ( \sqrt{{2 E}/{N_0}}\right ) + (M-2) \cdot 2 \cdot {\rm Q} \left ( \sqrt{{2 E}/{N_0}}\right ) \right ] \]

\[\Rightarrow \hspace{0.3cm} p_{\rm S} = \frac{2 \cdot (M-1)}{M} \cdot {\rm Q} \left ( \sqrt{{2 E}/{N_0}}\right ) =\frac{2 \cdot (M-1)}{M} \cdot {\rm Q} \left ( \sqrt{\frac{6 \cdot E_{\rm S}}{(M^2-1) \cdot N_0}}\right ) \hspace{0.05cm}.\]

Bei Verwendung des Graycodes (benachbarte Symbole unterscheiden sich jeweils um ein Bit) ist die Bitfehlerwahrscheinlichkeit $p_{\rm B}$ näherungsweise um den Faktor $b = \log_2 \ (M)$ kleiner als die Symbolfehlerwahrscheinlichkeit $p_{\rm S}$:

\[p_{\rm B} \approx \frac{p_{\rm S}}{b} = \frac{2 \cdot (M-1)}{M \cdot {\rm log_2}\, (M)} \cdot {\rm Q} \left ( \sqrt{{6 \cdot {\rm log_2}\, (M)}/({M^2-1 }) \cdot { E_{\rm B}}/{ N_0}}\right ) \hspace{0.05cm}.\]

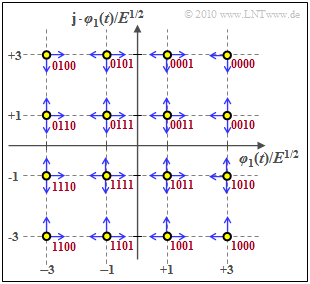
Quadrature amplitude modulation (M-QAM)

Signalraumkonstellation der 16-QAM

Die Quadraturamplitudenmodulation ($M$–QAM) ergibt sich durch je eine $M$–ASK für Inphase– und Quadraturkomponente ⇒ $M^2$ Signalraumpunkte.

Durch jedes Symbol werden nun $b = \log_2 (M)$ Binärzeichen (Bit) dargestellt. Die Grafik zeigt den Sonderfall $M = 16$ ⇒ $b = 4$. Rot eingezeichnet ist die Bitzuordnung bei Graycodierung (benachbarte Symbole unterscheiden sich jeweils um ein Bit).

Die mittlere Energie pro Symbol $(E_{\rm S})$ bzw. die mittlere Energie pro pro Bit $(E_{\rm B})$ kann man aus dem Ergebnis für die $M$–ASK einfach ableiten (beachten Sie in der Gleichung den Unterschied zwischen einer Energie $E$ und dem Erwartungswert $\rm E[\text{...}]$):

\[E_{\rm S} = {\rm E} \left [ |s_{i}|^2 \right ] = {\rm E} \left [ |s_{{\rm I}i}|^2 \right ] + {\rm E} \left [ |s_{{\rm Q}i}|^2 \right ] = 2 \cdot {\rm E} \left [ |s_{{\rm I}i}|^2 \right ]\]

\[\Rightarrow \hspace{0.3cm} E_{\rm S} = 2 \cdot \frac{M_{\rm I}^2-1}{3} \cdot E = \frac{2}{3} \cdot (M-1) \cdot E\hspace{0.01cm},\hspace{0.3cm}E_{\rm B} =\frac{2 \cdot (M-1)}{3 \cdot {\rm log_2}\, (M)} \cdot E \hspace{0.01cm}.\]

Daneben zeigt die M–stufige Quadraturamplitudenmodulation folgende Eigenschaften:

Als obere Schranke für die Symbolfehlerwahrscheinlichkeit kann die Union Bound herangezogen werden, wobei zu beachten ist, dass ein inneres Symbol in vier Richtungen verfälscht werden kann:

\[p_{\rm S} = {\rm Pr}({\cal{E}}) \le \left\{ \begin{array}{c} 4 \cdot p \\ 2 \cdot p \end{array} \right.\quad \begin{array}{*{1}c} {\rm f{\rm \ddot{u}r}} \hspace{0.15cm} M \ge 16 \hspace{0.05cm}, \\ {\rm f{\rm \ddot{u}r}} \hspace{0.15cm} M = 4 \hspace{0.05cm},\\ \end{array} \hspace{0.4cm} {\rm mit} \hspace{0.4cm} p = {\rm Q} \left ( \sqrt{{2 E}/{N_0}}\right ) \hspace{0.05cm}.\]

Berücksichtigt man, dass nur die $(b-2)^2$ inneren Punkte in vier Richtungen verfälscht werden, die vier Eckpunkte dagegen nur in zwei und die restlichen in drei Richtungen (blaue Pfeile in der Grafik), so erhält man mit $M = b^2$ die bessere Näherung

\[p_{\rm S} \approx {1}/{M} \cdot \big [(b - 2)^2 \cdot 4p + 4 \cdot 2p + 4 \cdot (b - 2) \cdot 3p \big ] = {p}/{M} \cdot \big [ 4 \cdot M - 16 \cdot \sqrt{M} + 16 + 8 + 12 \cdot \sqrt{M} - 24\big ] \]

\[\Rightarrow \hspace{0.3cm} p_{\rm S} \approx {4 \cdot p}/{M} \cdot \big [ M - \sqrt{M} \big ] = 4p \cdot \big [ 1 - {1}/{\sqrt{M}} \big ] \]

\[\Rightarrow\hspace{0.3cm} M = 16\hspace{-0.1cm}: \hspace{0.1cm} p_{\rm S} \approx 3 \cdot p = 3 \cdot {\rm Q} \big ( \sqrt{{2 E}/{N_0}}\big ) = 3 \cdot {\rm Q} \big ( \sqrt{{1/5 \cdot E_{\rm S}}/{ N_0}}\big ) \hspace{0.05cm}.\]

$\text{Fazit:}$ Bei der $M$–QAM gilt allgemein $E_{\rm B} = E_{\rm S}/\log_2 \hspace{0.05cm} (M)$ und bei Graycodierung zusätzlich $p_{\rm B} = p_{\rm S}/\log_2 \hspace{0.05cm} (M)$.

Damit erhält man für die mittlere Bitfehlerwahrscheinlichkeit:

\[p_{\rm B} \approx \frac{4 \cdot (1 - 1/\sqrt{M})}{ {\rm log_2}\hspace{0.05cm} (M)} \cdot {\rm Q} \left ( \sqrt{ \frac{3 \cdot {\rm log_2}\, (M)}{M-1 } \cdot { E_{\rm B} }/{ N_0} }\right ) \hspace{0.05cm}.\]

Die Näherung gilt für $M \le 16$ exakt, wenn – wie für die obere Grafik vorausgesetzt – keine "diagonalen Verfälschungen" auftreten.
Der Sonderfall "4–QAM" (ohne innere Symbole) wird in der Aufgabe 4.13 behandelt.

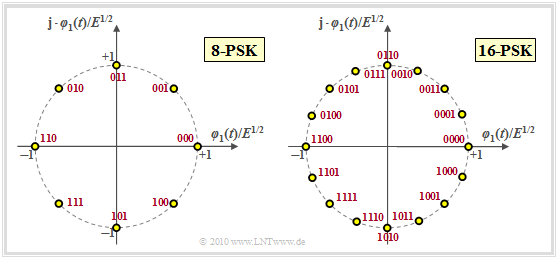
Multi-level phase–shift keying (M–PSK)

Bei mehrstufiger Phasenmodulation, wobei die Stufenzahl $M$ in der Praxis meist eine Zweierpotenz ist, liegen alle Signalraumpunkte auf einem Kreis mit Radius $E^{1/2}$ gleichmäßig verteilt. Damit gilt für die mittlere Symbolenergie $E_{\rm S} = E$ und für die mittlere Energie pro Bit $E_{\rm B} = E_{\rm S}/b = E/\hspace{-0.05cm}\log_2 \hspace{0.05cm} (M)$.

Signalraumkonstellation der 8–PSK und 16–PSK

Für die Inphase– und die Quadraturkomponente der Signalraumpunkte $\boldsymbol{s}_i$ gilt allgemein $(i = 0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, \hspace{0.05cm}M-1)$:

\[s_{{\rm I}i} = \cos \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right ) \hspace{0.05cm},\hspace{0.2cm} s_{{\rm Q}i} = \sin \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right ) \hspace{0.2cm}\Rightarrow \hspace{0.2cm} || \boldsymbol{ s}_i || = \sqrt{ s_{{\rm I}i}^2 + s_{{\rm Q}i}^2} = 1 \hspace{0.05cm}.\]

Der Phasenoffset ist in obiger Grafik jeweils zu $\phi_{\rm off} = 0$ gesetzt. Die 4–PSK mit $\phi_{\rm off} = \pi/4 \ (45^\circ)$ ist identisch mit der 4–QAM. Der Abstand zwischen zwei benachbarten Punkten ist in allen Fällen gleich:

\[d_{\rm min} = d_{\rm 0, \hspace{0.05cm}1} = d_{\rm 1, \hspace{0.05cm}2} = \hspace{0.05cm}\text{...} \hspace{0.05cm} = d_{M-1, \hspace{0.05cm}0} = 2 \cdot \sqrt{E} \cdot \sin (\pi/M)\]

\[\Rightarrow\hspace{0.3cm} M = 4\hspace{-0.1cm}:\hspace{0.1cm}d_{\rm min}/E^{1/2} = \sqrt{2} \approx 1.414 \hspace{0.05cm}, \hspace{0.8cm} M = 8\hspace{-0.1cm}:\hspace{0.1cm}d_{\rm min}/E^{1/2} \approx 0.765 \hspace{0.05cm},\hspace{0.8cm} M = 16\hspace{-0.1cm}:\hspace{0.1cm}d_{\rm min}/E^{1/2} \approx 0.390 \hspace{0.05cm}.\]

Die obere Schranke $p_{\rm UB}$ für die AWGN–Symbolfehlerwahrscheinlichkeit nach der Union Bound liefert:

\[p_{\rm S} = {\rm Pr}({\cal{E}}) \le 2 \cdot {\rm Q} \left ( \sin ({ \pi}/{ M}) \cdot \sqrt{ { {2E_{\rm S}}}/{ N_0} }\right ) = p_{\rm UB} \hspace{0.05cm}.\]

Man erkennt:

Für $M = 2$ (BPSK) erhält man daraus die Abschätzung $p_{\rm S} \le p_{\rm UB} =2 \cdot {\rm Q} \left ( \sqrt{ 2E_{\rm S}/{ N_0} }\right )$. Ein Vergleich mit der auf der BPSK–Seite angegebenen Gleichung $p_{\rm S} ={\rm Q} \left ( \sqrt{ 2E_{\rm S}/{ N_0} }\right )$ zeigt, dass in diesem Sonderfall die "Union Bound" als obere Schranke den doppelten Wert liefert.
Je größer $M$ ist, umso genauer nähert $p_{\rm UB}$ die exakte Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ an. Das interaktive Applet Mehrstufige PSK & Union Bound gibt auch die genauere, durch Simulation gewonnene Fehlerwahrscheinlichkeit an.

$\text{Fazit:}$ Die Schranke für die M–PSK–Bitfehlerwahrscheinlichkeit lautet (Graycode ⇒ rote Beschriftung vorausgesetzt):

\[p_{\rm B} \le \frac{2}{ {\rm log_2} \hspace{0.05cm}(M)} \cdot {\rm Q} \left ( \sqrt{ {\rm log_2} \hspace{0.05cm}(M)} \cdot \sin ({ \pi}/{ M}) \cdot \sqrt{ { {2E_{\rm B} } }/{ N_0} }\right ) \hspace{0.05cm}.\]

Diese Schranke muss man allerdings nur für $M > 4$ anwenden.
Für $M = 2$ (BPSK) und $M = 4$ (Identität zwischen 4–PSK und 4–QAM) kann man die Bitfehlerwahrscheinlichkeit exakt angeben:

$$p_{\rm B} = {\rm Q} \left ( \sqrt{ { {2E_{\rm B} } }/{ N_0} }\right ) \hspace{0.05cm}.$$

Binary frequency shift keying (2–FSK)

Auch diese Modulationsart mit Parameter $b = 1$ ⇒ $M = 2$ wurde bereits im Abschnitt FSK – Frequency Shift Keying des Buches "Modulationsverfahren" anhand der Bandpass–Signale ausführlich beschrieben.

Die beiden möglichen Signalformen werden im Bereich $0 \le t \le T$ durch zwei unterschiedliche Frequenzen dargestellt:

\[s_{\rm BP0}(t) \hspace{-0.1cm} = \hspace{-0.1cm} A \cdot \cos( 2\pi \cdot( f_{\rm T} + \Delta f_{\rm A})\cdot t)\hspace{0.05cm},\]

\[ s_{\rm BP1}(t) \hspace{-0.1cm} = \hspace{-0.1cm} A \cdot \cos( 2\pi \cdot( f_{\rm T} - \Delta f_{\rm A})\cdot t)\hspace{0.05cm}.\]

$f_{\rm T}$ bezeichnet die Trägerfrequenz und $\Delta f_{\rm A}$ den (einseitigen) Frequenzhub. Die mittlere Energie pro Symbol bzw. pro Bit ist jeweils gleich:

\[E_{\rm S} = E_{\rm B} = E = \frac{A^2 \cdot T}{2} \hspace{0.05cm}.\]

Hier soll nun die FSK im äquivalenten Tiefpass–Signalraum betrachtet werden. Dann gilt:

\[s_{\rm TP0}(t) \hspace{-0.1cm} = \hspace{-0.1cm} \sqrt{E/T} \cdot {\rm e}^{\hspace{0.05cm}+{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} 2\pi \hspace{0.03cm}\cdot \hspace{0.03cm} \Delta f_{\rm A} \hspace{0.03cm}\cdot t}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},\]

\[ s_{\rm TP1}(t) \hspace{-0.1cm} = \hspace{-0.1cm} \sqrt{E/T} \cdot {\rm e}^{\hspace{0.05cm}-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} 2\pi \hspace{0.03cm}\cdot \hspace{0.03cm} \Delta f_{\rm A} \hspace{0.03cm}\cdot t}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},\]

und für das innere Produkt erhält man

\[< \hspace{0.02cm} s_{\rm TP0}(t) \cdot s_{\rm TP1}(t) \hspace{0.02cm}> \hspace{0.1cm} = \hspace{-0.1cm} \int_{0}^{T} s_{\rm TP0}(t) \cdot s_{\rm TP1}^{\star}(t) \,{\rm d} t = A^2 \cdot \int_{0}^{T} {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} 4\pi \hspace{0.03cm}\cdot \hspace{0.03cm} \Delta f_{\rm A} \hspace{0.03cm}\cdot t} \,{\rm d} t = \frac{A^2}{{\rm j} \cdot 4\pi \cdot \Delta f_{\rm A}} \cdot \big [ {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} 4\pi \hspace{0.03cm}\cdot \hspace{0.03cm} \Delta f_{\rm A} \hspace{0.03cm}\cdot T} - 1 \big ] \hspace{0.05cm}.\]

$\text{Definition:}$ Der Modulationsindex $h = 2 \cdot \Delta f_{\rm A}\hspace{0.03cm}\cdot T$ ist das Verhältnis zwischen dem gesamten (beideseitigen) Frequenzhub $(2 \cdot \Delta f_{\rm A})$ und der Symbolrate $(1/T)$.

Die beiden Signale sind dann orthogonal, wenn dieses innere Produkt gleich Null ist:

\[< \hspace{0.02cm} s_{\rm TP0}(t) \cdot s_{\rm TP1}(t) \hspace{0.02cm}> \hspace{0.1cm} = \frac{A^2\cdot T}{{\rm j} \cdot 2\pi \cdot h} \cdot \left [ {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} 2h} - 1 \right ] = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} h = 2 \cdot \Delta f_{\rm A} \cdot T = 1,\hspace{0.1cm} 2, \hspace{0.1cm}3,\ \text{ ... }\hspace{0.05cm}.\]

Signalraumkonstellation der FSK, falls $h$ ganzzahlig

Setzt man den Modulationsindex $h$ als ganzzahlig voraus, so lassen sich die Tiefpass–Signale in der Form

\[s_{\rm TP0}(t) = \sqrt{E} \cdot \xi_1(t) \hspace{0.05cm},\]

\[s_{\rm TP1}(t) = \sqrt{E} \cdot \xi_2(t)\]

mit komplexen Basisfunktionen darstellen:

\[\xi_1(t) = \sqrt{1/T} \cdot {\rm e}^{\hspace{0.05cm}+{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} \pi \hspace{0.03cm}\cdot \hspace{0.03cm} h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},\]

\[ \xi_2(t)= \sqrt{1/T} \cdot {\rm e}^{\hspace{0.05cm}-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} \pi \hspace{0.03cm}\cdot \hspace{0.03cm} h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T \hspace{0.05cm}.\]

Es ergibt sich die hier skizzierte Signalraumdarstellung der binären FSK.

$\text{Fazit:}$

Bei ganzzahligem Modulationsindex $h$ sind die Tiefpass-Signale $s_{\rm TP0}(t)$ und $s_{\rm TP1}(t)$ der binären FSK zueinander orthogonal.

Damit ergibt sich für die Symbolfehlerwahrscheinlichkeit (Herleitung in der Grafik):

\[p_{\rm S} = {\rm Pr}({\cal{E} }) = {\rm Q} \left ( \sqrt{ { {E_{\rm S} } }/{ N_0} }\right ) \hspace{0.05cm}.\]

Die Bitfehlerwahrscheinlichkeit hat den gleichen Wert: $p_{\rm B} = p_{\rm S}$.

Hinweis: Im Gegensatz zur Darstellung in [KöZ08]^[1] ist hier der Frequenzhub $\Delta f_{\rm A}$ einseitig definiert. Deshalb unterscheiden sich die Gleichungen teilweise um den Faktor $2$. Arbeitet man jedoch mit dem Modulationsindex $h$, so gibt es keine Unterschiede.

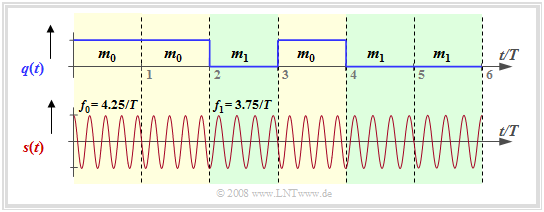
Minimum Shift Keying (MSK)

Unter Minimum Shift Keying (MSK) versteht man ein binäres FSK–System mit dem Modulationsindex $h = 0.5$ ⇒ Frequenzhub $\Delta f_{\rm A} = 1/(2T)$. Die Grafik zeigt ein MSK–Signal für die Trägerfrequenz $ f_{\rm T} = 4/T$:

Die beiden Frequenzen innerhalb des Sendsignals sind $ f_{\rm 0} = f_{\rm T} + 1/(4T)$ zur Darstellung der Nachricht $m_0$ (gelbe Hinterlegung) sowie $ f_{\rm 1} = f_{\rm T} -1/(4T)$ ⇒ Nachricht $m_1$ (grüne Hinterlegung).
In der Grafik ist auch eine kontinuierliche Phasenanpassung bei den Übergängen berücksichtigt, um die Signalbandbreite weiter zu verringern. Man spricht dann von Continuous Phase Modulation (CPM).

Quellensignal und Bandpass–MSK–Signal

Ohne diese Phasenanpassung lauten die beiden Bandpass–Signalformen:

\[s_{\rm BP0}(t) = \sqrt{2E/T} \cdot \cos( 2\pi f_0 t)\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},\]

\[ s_{\rm BP1}(t) = \sqrt{2E/T} \cdot \cos( 2\pi f_1 t)\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm}.\]

Bildet man das innere Produkt der Bandpass–Signale, so erhält man mit $f_{\rm \Delta} = f_0 - f_1$ und $f_{\rm \Sigma} = f_0 + f_1$:

\[< \hspace{0.02cm} s_{\rm BP0}(t) \hspace{0.2cm} \cdot \hspace{0.2cm} s_{\rm BP1}(t) \hspace{0.02cm}> \hspace{0.2cm} = {2E}/{T} \cdot \int_{0}^{T} \cos( 2\pi f_0 t) \cdot \cos( 2\pi f_1 t)\,{\rm d} t = {E}/{T} \cdot \int_{0}^{T} \cos( 2\pi f_{\rm \Delta} t) \,{\rm d} t + {E}/{T} \cdot \int_{0}^{T} \cos( 2\pi f_{\rm \Sigma} t) \,{\rm d} t\]

\[ \Rightarrow \hspace{0.3cm}< \hspace{0.02cm} s_{\rm BP0}(t) \hspace{0.2cm} \cdot \hspace{0.2cm} s_{\rm BP1}(t) \hspace{0.02cm}> \hspace{0.2cm} = {E}/{T} \cdot \int_{0}^{T} \hspace{-0.1cm} \cos( \pi \cdot {t}/{T}) \,{\rm d} t + {E}/{T} \cdot \int_{0}^{T} \hspace{-0.1cm}\cos( 2\pi \cdot 2 f_{\rm T} \cdot t) \,{\rm d} t \hspace{0.05cm}.\]

Das erste Integral ist Null $($Integral über "Cosinus" von $0$ bis $\pi)$. Für $f_{\rm T} \gg 1/T$, was man in der Praxis voraussetzen kann, verschwindet auch das zweite Integral. Damit erhält man für das innere Produkt:

$$< \hspace{0.02cm} s_{\rm BP0}(t) \cdot s_{\rm BP1}(t) \hspace{0.02cm}> \hspace{0.2cm}= 0 \hspace{0.05cm}.$$

$\text{Fazit:}$

Damit ist gezeigt, dass für den Modulationsindex $h = 0.5$ (also MSK) und allen Vielfachen hiervon die beiden Bandpass–Signale orthogonal sind.
Mit den neuen reellen Basisfunktionen

\[\varphi_1(t) = \sqrt{2/T} \cdot \cos( 2\pi f_0 t)\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},\]

\[ \varphi_2(t) = \sqrt{2/T} \cdot \cos( 2\pi f_1 t)\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\]

erhält man die genau gleiche Signalraumkonstellation wie für geradzahliges $h = 1, 2, 3, \ \text{ ...}$.