Difference between revisions of "Digital Signal Transmission/Carrier Frequency Systems with Non-Coherent Demodulation"
| Line 134: | Line 134: | ||
::<math>r_1 = \sqrt{E} \cdot {\rm e}^{{\rm j}\phi} + n_1\hspace{0.3cm} \Rightarrow \hspace{0.3cm}y_1 = |r_1|\hspace{0.15cm}{\rm is}\hspace{0.15cm}{\rm Rice}\hspace{0.15cm}{\rm distributed} | ::<math>r_1 = \sqrt{E} \cdot {\rm e}^{{\rm j}\phi} + n_1\hspace{0.3cm} \Rightarrow \hspace{0.3cm}y_1 = |r_1|\hspace{0.15cm}{\rm is}\hspace{0.15cm}{\rm Rice}\hspace{0.15cm}{\rm distributed} | ||
\hspace{0.05cm},</math> | \hspace{0.05cm},</math> | ||
| − | ::<math> r_2 = n_2\hspace{0.3cm} \Rightarrow \hspace{0.3cm}y_2 = |r_2|\hspace{0.15cm}{\rm | + | ::<math> r_2 = n_2\hspace{0.3cm} \Rightarrow \hspace{0.3cm}y_2 = |r_2|\hspace{0.15cm}{\rm is}\hspace{0.15cm}{\rm Rayleigh}\hspace{0.15cm}{\rm distributed} |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | Here, $E$ due to $M = 2$ represents the <i>symbol energy</i> $(E_{\rm S})$ and the <i>bit energy</i> $(E_{\rm B})$ equally, and $n_1$ and $n_2$ are uncorrelated complex noise variables with mean zero and variance $2 \cdot \sigma_n^2$. Thus, the [[Theory_of_Stochastic_Signals/Two-Dimensional_Random_Variables#Joint_probability_density_function|"joint probability density function"]] is: | |
::<math>p_{y_1,\hspace{0.03cm} y_2 \hspace{0.03cm}| \hspace{0.03cm}m} ( \eta_1, \eta_2 \hspace{0.05cm}| \hspace{0.05cm}m_0) = | ::<math>p_{y_1,\hspace{0.03cm} y_2 \hspace{0.03cm}| \hspace{0.03cm}m} ( \eta_1, \eta_2 \hspace{0.05cm}| \hspace{0.05cm}m_0) = | ||
p_{y_1 \hspace{0.01cm}| \hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm}| \hspace{0.05cm}m_0) \cdot | p_{y_1 \hspace{0.01cm}| \hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm}| \hspace{0.05cm}m_0) \cdot | ||
| Line 148: | Line 148: | ||
\cdot {\rm e }^{ - \eta_2^2 /({2 \sigma_n^2}) } \hspace{0.05cm}.</math> | \cdot {\rm e }^{ - \eta_2^2 /({2 \sigma_n^2}) } \hspace{0.05cm}.</math> | ||
| − | + | The error probability is generally obtained as follows: | |
::<math>{\rm Pr}({\cal{E}}) = \int_{0}^{\infty} \int_{\eta_1}^{\infty} | ::<math>{\rm Pr}({\cal{E}}) = \int_{0}^{\infty} \int_{\eta_1}^{\infty} | ||
| Line 156: | Line 156: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Conclusion:}$ For the '''error probability with non-coherent demodulation of the binary FSK''', one obtains after some mathematical transformations the surprisingly simple result |
::<math>p_{\rm S} = {\rm Pr}({\cal{E} }) = {1}/{2} \cdot {\rm e}^{-E_{\rm S}/(2 N_0)} | ::<math>p_{\rm S} = {\rm Pr}({\cal{E} }) = {1}/{2} \cdot {\rm e}^{-E_{\rm S}/(2 N_0)} | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | For comparison, the result for '''coherent demodulation''' is given again: | |
::<math>p_{\rm S} = {\rm Pr}({\cal{E} }) = {\rm Q}(\sqrt{ E_{\rm S}/N_0}) | ::<math>p_{\rm S} = {\rm Pr}({\cal{E} }) = {\rm Q}(\sqrt{ E_{\rm S}/N_0}) | ||
\hspace{0.05cm}.</math>}} | \hspace{0.05cm}.</math>}} | ||
| Line 167: | Line 167: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Derivation:}$ The result taken in advance is now to be derived in some calculation steps. We start from the following equations: |
:$${\rm Pr}({\cal{E} }) = \int_{0}^{\infty} p_{y_1 \hspace{0.01cm} \vert\hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm} \vert \hspace{0.05cm}m_0) \cdot \int_{\eta_1}^{\infty} | :$${\rm Pr}({\cal{E} }) = \int_{0}^{\infty} p_{y_1 \hspace{0.01cm} \vert\hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm} \vert \hspace{0.05cm}m_0) \cdot \int_{\eta_1}^{\infty} | ||
p_{y_2 \hspace{0.03cm}\vert \hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm}\vert \hspace{0.05cm}m_0)\,\,{\rm d} \eta_2\,\,{\rm d} \eta_1 | p_{y_2 \hspace{0.03cm}\vert \hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm}\vert \hspace{0.05cm}m_0)\,\,{\rm d} \eta_2\,\,{\rm d} \eta_1 | ||
| − | \hspace{0.05cm},\hspace{0.5cm}\text{ | + | \hspace{0.05cm},\hspace{0.5cm}\text{with}$$ |
:$$p_{y_1 \hspace{0.01cm}\vert \hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm}\vert \hspace{0.05cm}m_0) = {\eta_1}/{\sigma_n^2} \cdot {\rm e }^{ - ({\eta_1^2 + E})/({2 \sigma_n^2}) }\cdot {\rm I }_0 \left [{\eta_1 \cdot \sqrt{E} }/{ \sigma_n^2}\right ] \hspace{0.05cm},\hspace{0.5cm}p_{y_\hspace{0.01cm}\vert \hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm}\vert \hspace{0.05cm}m_0) = {\eta_2}/{\sigma_n^2} \cdot {\rm e }^{ - \eta_2^2 /({2 \sigma_n^2}) } \hspace{0.05cm}.$$ | :$$p_{y_1 \hspace{0.01cm}\vert \hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm}\vert \hspace{0.05cm}m_0) = {\eta_1}/{\sigma_n^2} \cdot {\rm e }^{ - ({\eta_1^2 + E})/({2 \sigma_n^2}) }\cdot {\rm I }_0 \left [{\eta_1 \cdot \sqrt{E} }/{ \sigma_n^2}\right ] \hspace{0.05cm},\hspace{0.5cm}p_{y_\hspace{0.01cm}\vert \hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm}\vert \hspace{0.05cm}m_0) = {\eta_2}/{\sigma_n^2} \cdot {\rm e }^{ - \eta_2^2 /({2 \sigma_n^2}) } \hspace{0.05cm}.$$ | ||
| − | <b>(1)</b> | + | <b>(1)</b> The inner integral gives the probability that the Rayleigh distributed random variable $\eta_2$ is larger than $\eta_1$ – see solution to [[Aufgaben:Exercise_4.17Z:_Rayleigh_and_Rice_Distribution|"Exercise 4.17Z"]]: |
:$$\int_{\eta_1}^{\infty} p_{y_2 \hspace{0.03cm}\vert\hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm}\vert \hspace{0.05cm}m_0)\,\,{\rm d} \eta_2 = | :$$\int_{\eta_1}^{\infty} p_{y_2 \hspace{0.03cm}\vert\hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm}\vert \hspace{0.05cm}m_0)\,\,{\rm d} \eta_2 = | ||
| Line 183: | Line 183: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | <b>(2)</b> | + | <b>(2)</b> With the (arbitrary) substitutions $C_0^2 = E/4$ and $\sigma_0^2 = \sigma_n^2/2$, we obtain: |
:$${\rm Pr}({\cal{E} }) = \int_{0}^{\infty} \frac{\eta_1}{2 \cdot \sigma_0^2} | :$${\rm Pr}({\cal{E} }) = \int_{0}^{\infty} \frac{\eta_1}{2 \cdot \sigma_0^2} | ||
| Line 192: | Line 192: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | <b>(3)</b> | + | <b>(3)</b> By shifting fractions in front of the integral, we succeed that the integrand again describes a [[Theory_of_Stochastic_Signals/Further_Distributions#Rice_PDF|"Rice distribution"]]: |
::<math>{\rm Pr}({\cal{E} }) = {1}/{2} \cdot {\rm exp } \left [ - \frac{ C_0^2}{2 \sigma_0^2}\right ] \cdot \int\limits_{0}^{\infty} \frac{\eta_1}{ \sigma_0^2} | ::<math>{\rm Pr}({\cal{E} }) = {1}/{2} \cdot {\rm exp } \left [ - \frac{ C_0^2}{2 \sigma_0^2}\right ] \cdot \int\limits_{0}^{\infty} \frac{\eta_1}{ \sigma_0^2} | ||
| Line 199: | Line 199: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | <b>(4)</b> | + | <b>(4)</b> The integrand now describes the Rice PDF. The integral over the entire definition area from $0$ to $+\infty$ yields the value one, as for any PDF, so that holds: |
::<math>{\rm Pr}({\cal{E} }) = {1}/{2} \cdot {\rm exp } \left [ - \frac{ C_0^2}{2 \sigma_0^2}\right ]\hspace{0.05cm}.</math> | ::<math>{\rm Pr}({\cal{E} }) = {1}/{2} \cdot {\rm exp } \left [ - \frac{ C_0^2}{2 \sigma_0^2}\right ]\hspace{0.05cm}.</math> | ||
| − | <b>(5)</b> | + | <b>(5)</b> Finally, with $C_0^2 = E/4$ and $\sigma_0^2 = \sigma_n^2/2$ and the generally valid relation $\sigma_n^2 = N_0$, we obtain: |
:$${\rm Pr}({\cal{E} }) | :$${\rm Pr}({\cal{E} }) | ||
= {1}/{2} \cdot {\rm exp } \left [ - \frac{ C_0^2}{2 \sigma_0^2}\right ] = {1}/{2} \cdot {\rm exp } \left [ - \frac{ E_{\rm S}/4}{N_{\rm 0}/2}\right ] \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm S} = {\rm Pr}({\cal{E} }) = {1}/{2} \cdot {\rm e}^{-E_{\rm S}/(2 N_0)}\hspace{0.05cm}.$$ | = {1}/{2} \cdot {\rm exp } \left [ - \frac{ C_0^2}{2 \sigma_0^2}\right ] = {1}/{2} \cdot {\rm exp } \left [ - \frac{ E_{\rm S}/4}{N_{\rm 0}/2}\right ] \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm S} = {\rm Pr}({\cal{E} }) = {1}/{2} \cdot {\rm e}^{-E_{\rm S}/(2 N_0)}\hspace{0.05cm}.$$ | ||
| − | <b>q.e.d.</b> $E_{\rm S}$ | + | <b>q.e.d.</b> $E_{\rm S}$ here indicates the average signal energy per symbol, which is equal to the normalization energy $E$ for FSK.}}<br> |
| − | [[File:P ID2088 Dig T 4 5 S3b version1.png|right|frame|FSK- | + | [[File:P ID2088 Dig T 4 5 S3b version1.png|right|frame|FSK error probability for coherent and non-coherent demodulation|class=fit]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 2:}$ The graph compares the error probability curves of both demodulation methods as a function of the AWGN quotient $E_{\rm S}/N_0$. |
| − | + | One can see: | |
| − | * | + | *The non-coherent FSK (red curve) requires a $0.8 \ \rm dB$ larger $E_{\rm S}/N_0$ compared to the coherent FSK (blue curve) at $p_{\rm S}= 10^{-5}$. |
| − | * | + | *At $p_{\rm S}= 10^{-3}$ the distance is even $1.3 \ \rm dB$.<br> |
| − | * | + | *In contrast, the distance between the coherent binary FSK from the coherent BPSK is always $1.3 \ \rm dB$ regardless of the error probability. |
<br clear =all>}} | <br clear =all>}} | ||
| − | == | + | == Non-coherent demodulation of multi-level FSK== |
<br> | <br> | ||
| − | [[File:P ID2089 Dig T 4 5 S4a version1.png|right|frame| | + | [[File:P ID2089 Dig T 4 5 S4a version1.png|right|frame|Orthogonal $M$–level FSK for $M= 3$]] |
| − | + | We now consider the message set $\{m_1, m_2,\hspace{0.05cm}\text{ ...} \hspace{0.05cm}, m_{M}\}$ and denote $M$ as the number of levels. | |
| − | * | + | *As in the case of binary FSK, a prerequisite for the application of the modulation process <i>"Frequency Shift Keying"</i> and at the same time of a non-coherent demodulator is an integer modulation index $h$.<br> |
| − | *In | + | *In this case, the $M$–level FSK is orthogonal and a signal space constellation results as shown in the adjacent diagram for the special case $M = 3$. <br><br> |
| − | + | The non-coherent demodulator is sketched below. Compared to the [[Digital_Signal_Transmission/Carrier_Frequency_Systems_with_Non-Coherent_Demodulation#Non-coherent_demodulation_of_binary_FSK_.282.E2.80.93FSK.29|"receiver structure for binary FSK"]], this receiver differs only by $M$ branches instead of only two, which provide the comparison values $y_1$, $y_2$, ... , $y_M$.<br> | |
| − | [[File:P ID2090 Dig T 4 5 S4b version1.png|center|frame| | + | [[File:P ID2090 Dig T 4 5 S4b version1.png|center|frame|Non-coherent receiver structure for $M$–level FSK|class=fit]] |
| − | + | To calculate the error probability, we assume that $m_1$ was sent. This means that the decision is correct if the largest detection output value is $y_1$: | |
::<math>{\rm Pr}({\cal{C}}) \hspace{-0.1cm} = \hspace{-0.1cm} {\rm Pr} \big [ (y_2 < y_1) \cap (y_3 < y_1) \cap ... \cap (y_{M} < y_1) | ::<math>{\rm Pr}({\cal{C}}) \hspace{-0.1cm} = \hspace{-0.1cm} {\rm Pr} \big [ (y_2 < y_1) \cap (y_3 < y_1) \cap ... \cap (y_{M} < y_1) | ||
| Line 241: | Line 241: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Conclusion:}$ |
| − | * | + | * The '''error probability of M–level FSK in non-coherent demodulation''' is equal to ${\rm Pr}({\cal{E} }) = 1 - {\rm Pr}({\cal{C} })$. |
| − | * | + | *In the following, it is shown that ${\rm Pr}({\cal{C} })$ can be represented as follows: |
::<math>{\rm Pr}({\cal{C} }) = \sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot \frac{1}{i+1} \cdot {\rm exp } \left [ - \frac{i \cdot E_{\rm S} } | ::<math>{\rm Pr}({\cal{C} }) = \sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot \frac{1}{i+1} \cdot {\rm exp } \left [ - \frac{i \cdot E_{\rm S} } | ||
{(i+1) \cdot N_0}\right ] | {(i+1) \cdot N_0}\right ] | ||
| − | \hspace{0.05cm}\hspace{0.5cm} \text{ | + | \hspace{0.05cm}\hspace{0.5cm} \text{with}\hspace{0.5cm} E_{\rm S} = E_{\rm B} \cdot {\rm log_2}(M)\hspace{0.05cm}.</math> |
| − | * | + | *In the special case $M = 2$, of course, the result obtained in the [[Digital_Signal_Transmission/Carrier_Frequency_Systems_with_Coherent_Demodulation|"last section"]] is again obtained: |
::<math>p_{\rm S} = {\rm Pr}({\cal{E} }) = {1}/{2} \cdot {\rm e}^{-E_{\rm S}/(2 N_0)} | ::<math>p_{\rm S} = {\rm Pr}({\cal{E} }) = {1}/{2} \cdot {\rm e}^{-E_{\rm S}/(2 N_0)} | ||
| Line 256: | Line 256: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Derivation:}$ The result taken in advance shall now be derived in some calculation steps. We assume that $m_1$ has been sent. This means that the decision is correct if the largest detection output value is $y_1$. Otherwise, there are certain analogies to the derivation of the [[Digital_Signal_Transmission/Carrier_Frequency_Systems_with_Non-Coherent_Demodulation#Error_probability_with_non-coherent_2.E2.80.93FSK_demodulation|"BFSK error probability"]].<br> |
| − | <b>(1)</b> | + | <b>(1)</b> Using the conditional probability density $p_{y_1 \hspace{0.01cm} \vert\hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm} \vert \hspace{0.05cm}m_1)$, we obtain: |
::<math>{\rm Pr}({\cal{C} }) = \int_{0}^{\infty} {\rm Pr} \left [ \hspace{0.1cm} \bigcap\limits_{k = 2}^M (y_k < y_1) | ::<math>{\rm Pr}({\cal{C} }) = \int_{0}^{\infty} {\rm Pr} \left [ \hspace{0.1cm} \bigcap\limits_{k = 2}^M (y_k < y_1) | ||
| Line 264: | Line 264: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | <b>(2)</b> | + | <b>(2)</b> The decision values $y_2$, $y_3$, ... , $y_M$ are statistically independent for given $y_1$. Therefore: |
::<math>{\rm Pr}({\cal{C} }) = \int_{0}^{\infty} \left \{ {\rm Pr} \big [ (y_2 < y_1) | ::<math>{\rm Pr}({\cal{C} }) = \int_{0}^{\infty} \left \{ {\rm Pr} \big [ (y_2 < y_1) | ||
| Line 270: | Line 270: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | <b>(3)</b> | + | <b>(3)</b> The selected value $y_2$ conditioned on $m_1$ has a Rayleigh distribution with parameter $\sigma_n^2$: |
::<math>{\rm Pr} \big [ (y_2 < y_1) | ::<math>{\rm Pr} \big [ (y_2 < y_1) | ||
| − | \hspace{0.05cm} \vert \hspace{0.05cm}y_1 = \eta_1, m = m_1\big ] \hspace{-0.1cm} = \hspace{-0.1cm} \int_{0}^{\eta_1} p_{y_2 \hspace{0.01cm} \vert\hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm} \vert \hspace{0.05cm}m_1)\,\,{\rm d} \eta_2= 1 - {\rm exp } \big [ - {\eta_1^2 }/({2 \sigma_n^2})\big ] = 1 - a \hspace{0.2cm}{\rm( | + | \hspace{0.05cm} \vert \hspace{0.05cm}y_1 = \eta_1, m = m_1\big ] \hspace{-0.1cm} = \hspace{-0.1cm} \int_{0}^{\eta_1} p_{y_2 \hspace{0.01cm} \vert\hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm} \vert \hspace{0.05cm}m_1)\,\,{\rm d} \eta_2= 1 - {\rm exp } \big [ - {\eta_1^2 }/({2 \sigma_n^2})\big ] = 1 - a \hspace{0.2cm}{\rm(abbreviation)} |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | <b>(4)</b> | + | <b>(4)</b> Now we are looking for the expression $(1 -a)^{M-1}$, for which with the abbreviation from <b>(3)</b> holds: |
::<math> (1-a)^{M-1} \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot (-1)^i \cdot a^i = \sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot {\rm exp } \left [ - \frac{i \cdot \eta_1^2 }{2 \sigma_n^2}\right ] | ::<math> (1-a)^{M-1} \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot (-1)^i \cdot a^i = \sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot {\rm exp } \left [ - \frac{i \cdot \eta_1^2 }{2 \sigma_n^2}\right ] | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | <b>(5)</b> $y_1$ | + | <b>(5)</b> $y_1$ has a [[Digital_Signal_Transmission/Carrier_Frequency_Systems_with_Non-Coherent_Demodulation#Rayleigh_and_Rice_Distribution|"Rice distribution"]] conditioned on $m=m_1$. Thus, the probability of a correct decision can be expressed in the following form: |
::<math>{\rm Pr}({\cal{C} }) \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot \int_{0}^{\infty} {\rm exp } \left [ - \frac{i \cdot \eta_1^2 }{2 \sigma_n^2}\right ] \cdot \frac{\eta_1}{ \sigma_n^2}\cdot | ::<math>{\rm Pr}({\cal{C} }) \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot \int_{0}^{\infty} {\rm exp } \left [ - \frac{i \cdot \eta_1^2 }{2 \sigma_n^2}\right ] \cdot \frac{\eta_1}{ \sigma_n^2}\cdot | ||
| Line 288: | Line 288: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | <b>(6)</b> | + | <b>(6)</b> Substitutions succeed in shaping the integrand according to the Rice distribution. Since each probability density integrates to one, we obtain: |
::<math>{\rm Pr}({\cal{C} }) = \sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot \frac{1}{i+1} \cdot {\rm exp } \left [ - \frac{i \cdot E_{\rm S} } | ::<math>{\rm Pr}({\cal{C} }) = \sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot \frac{1}{i+1} \cdot {\rm exp } \left [ - \frac{i \cdot E_{\rm S} } | ||
{(i+1) \cdot N_0}\right ] | {(i+1) \cdot N_0}\right ] | ||
| − | \hspace{0.05cm}\hspace{0.5cm} \text{ | + | \hspace{0.05cm}\hspace{0.5cm} \text{with}\hspace{0.5cm} E_{\rm S} = E_{\rm B} \cdot {\rm log_2}(M)\hspace{0.05cm}.</math> |
| − | <b>(7)</b> | + | <b>(7)</b> The special case $M = 2$ leads to exactly the same result as calculated for the binary FSK: |
::<math>{\rm Pr}({\cal{C} }) = (-1)^0 \cdot {2-1 \choose 0 } \cdot \frac{1}{0+1} \cdot {\rm exp } \left [ - \frac{0 \cdot E_{\rm S} } | ::<math>{\rm Pr}({\cal{C} }) = (-1)^0 \cdot {2-1 \choose 0 } \cdot \frac{1}{0+1} \cdot {\rm exp } \left [ - \frac{0 \cdot E_{\rm S} } | ||
| Line 303: | Line 303: | ||
\hspace{0.05cm}.</math>}} | \hspace{0.05cm}.</math>}} | ||
| − | == | + | == Exercises for the chapter== |
<br> | <br> | ||
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_4.17:_Non-Coherent_On-Off_Keying|Exercise 4.17: Non-Coherent On-Off Keying]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_4.17Z:_Rayleigh_and_Rice_Distribution|Exercise 4.17Z: Rayleigh and Rice Distribution]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_4.18:_Non-Coherent_FSK_Demodulation|Exercise 4.18: Non-Coherent FSK Demodulation]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_4.18Z:_BER_of_Coherent_and_Non-Coherent_FSK|Exercise 4.18Z: BER of Coherent and Non-Coherent FSK]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_4.19:_Orthogonal_Multilevel_FSK|Exercise 4.19: Orthogonal Multilevel FSK]] |
{{Display}} | {{Display}} | ||
Revision as of 15:16, 16 August 2022
Contents
Rayleigh and Rice Distribution
The estimation of the phase angle from the incoming signal, which is required for coherent demodulation, is not possible or only possible to a limited extent in many applications. For example, the movement of a mobile subscriber at high speed leads to very rapid temporal changes in the phase angle $\phi$, which makes its sufficiently accurate determination difficult or even impossible.
This fact leads to the non-coherent demodulation processes with the advantage of reduced complexity, but with increased probability of falsification. In the derivation of the equations one encounters two probability density functions, which are given here in advance:
- The Rayleigh distribution is obtained for the PDF of the random variable $y$ with realization $\eta$, which is obtained from the two Gaussian distributed and statistically independent components $u$ and $v$ (both with the same standard deviation $\sigma_n)$ as follows:
- \[y = \sqrt{u^2 + v^2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_y (\eta) ={\eta}/{\sigma_n^2} \cdot {\rm exp } \left [ - {\eta^2}/{ (2\sigma_n^2)}\right ] \hspace{0.05cm}.\]
- The Rice distribution is obtained under the same boundary conditions for the case where a constant $C$ is added to one of the components $($either $u$ or $v)$:
- \[y = \sqrt{(u+C)^2 + v^2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_y (\eta) = {\eta}/{\sigma_n^2} \cdot {\rm exp } \left [ - ({\eta^2 + C^2})/(2 \sigma_n^2) \right ] \cdot {\rm I }_0 \left [{\eta \cdot C}/{ \sigma_n^2}\right ] \hspace{0.05cm}.\]
- The Rice distribution uses the modified zero-order Bessel function, whose definition and series expansion are as follows:
- \[{\rm I }_0 (x) = \frac{1}{ 2\pi} \cdot \int_{0}^{2\pi} {\rm e }^{-x \hspace{0.03cm}\cdot \hspace{0.03cm}\cos(\alpha)} \,{\rm d} \alpha \hspace{0.2cm} \approx \hspace{0.2cm} \sum_{k = 0}^{\infty} \frac{(x/2)^{2k}}{k! \cdot \Gamma (k+1)} \hspace{0.05cm}.\]
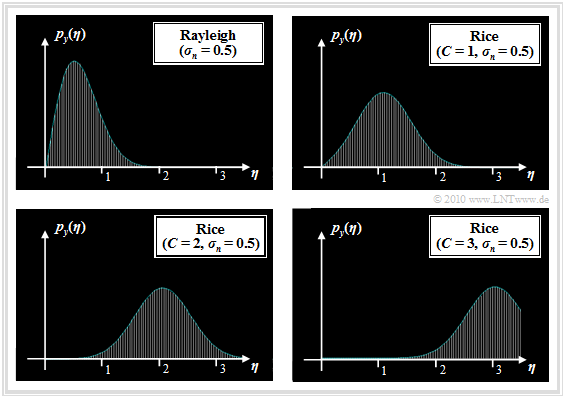
The graph shows the probability density functions of Rayleigh and Rice distributions.
To this representation it is to be noted:
- The Rice distribution is determined by the two parameters $C$ and $\sigma_n$. With $C = 0$, the Rice PDF is identical to the Rayleigh PDF.
- The Rayleigh PDF with larger $\sigma_n$ is of the same shape as shown for $\sigma_n = 0.5$, but wider and lower in the ratio of standard deviation.
- $\sigma_n$ indicates the standard deviation of the two Gaussian distributed random variables $u$ and $v$ and not the standard deviation of the Rayleigh distributed random variable $y$. Rather, the following applies to the latter:
- \[\sigma_y = \sigma_n \cdot \sqrt{2 - {\pi}/{2 }} \hspace{0.2cm} \approx \hspace{0.2cm} 0.655 \cdot \sigma_n \hspace{0.05cm}.\]
- The Rayleigh distribution is extremely asymmetric, recognizable by the (relatively) large value for the "third order central moment" ⇒ Charlier's skewness:
- $$\mu_3/\sigma_y \approx 0.27.$$
- The Rice distribution is more symmetric the larger the ratio $C/\sigma_n$ is. For $C/\sigma_n \ge 4$, $\mu_3 \approx 0$. The larger $C/\sigma_n$ is, the more the Rice distribution $($with $C$, $\sigma_n)$ approaches a "Gaussian distribution" with mean $C$ and standard deviation $\sigma_n$:
- \[p_y (\eta) \approx \frac{1}{\sqrt{2\pi} \cdot \sigma_n} \cdot {\rm exp } \left [ - \frac{(\eta - C)^2}{2 \sigma_n^2}\right ] \hspace{0.3cm} \Rightarrow \hspace{0.3cm} m_y = C\hspace{0.05cm},\hspace{0.2cm}\sigma_y = \sigma_n \hspace{0.05cm}.\]
Non-coherent demodulation of on–off keying
We consider "on–off keying" (or 2–ASK) in the equivalent low-pass range.
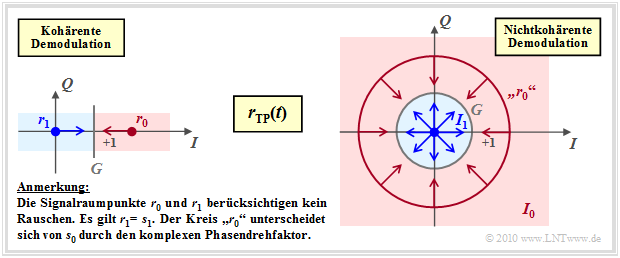
- In the case of coherent demodulation (left graph), the signal space constellation of the received signal is the same as that of the transmitted signal and consists of two points.
- The decision boundary $G$ lies in the middle between these points $\boldsymbol{r}_0$ and $\boldsymbol{r}_1$.
- The arrows mark the rough direction of noise vectors that may cause transmission errors.
On the other hand, for non-coherent demodulation (right graph):
- The point $\boldsymbol{r}_1 = \boldsymbol{s}_1 = 0$ is still preserved. On the other hand, $\boldsymbol{r}_0 = \boldsymbol{s}_0 \cdot {\rm e}^{\hspace{0.02cm}{\rm j}\hspace{0.03cm}\phi}$ can lie on any point of the circle around $\boldsymbol{s}_0$, since $\phi$ is unknown.
- The decision process taking into account the AWGN noise can now be interpreted in two dimensions, as indicated by the arrows in the right graph.
- The decision area $I_1$ is a circle whose radius $G$ is an optimizable parameter. The decision area $I_0$ lies outside the circle.
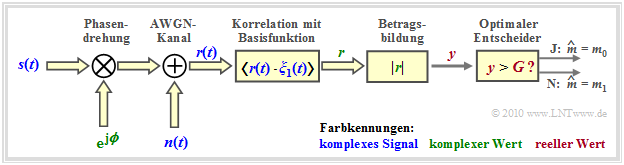
Thus, the structure of the optimal OOK receiver (in the equivalent low–pass range) is fixed. According to this second graph:
- The input signal $\boldsymbol{r}(t) = \boldsymbol{s}(t) \cdot {\rm e}^{\hspace{0.02cm}{\rm j}\hspace{0.03cm}\phi} + \boldsymbol{n}(t)$ is generally complex because of the phase angle $\phi$ and because of the complex noise term $\boldsymbol{n}(t)$. Consequently, what is required now is the correlation between the complex received signal $\boldsymbol{r}(t)$ and a complex basis function $\boldsymbol{\xi}_1(t)$.
- The result is the (complex) detector value $\boldsymbol{r}$, from which the amount $y = |\boldsymbol{r}(t)|$ is formed as a real decision input variable.
- If the decision value $y \gt G$, then $m_0$ is output as the estimated value, otherwise $m_1$. Thus, the error probability for equally probable symbols is:
- \[p_{\rm S} = {\rm Pr}({\cal{E}}) = {1}/{ 2} \cdot \int_{0}^{G} p_{y\hspace{0.05cm}\vert \hspace{0.05cm}m} (\eta \hspace{0.05cm}|\hspace{0.05cm} m_0) \,{\rm d} \eta + {1}/{ 2} \cdot \int_{G}^{\infty} p_{y\hspace{0.05cm}\vert \hspace{0.05cm}m} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} m_1) \,{\rm d} \eta \hspace{0.05cm}.\]
- However, due to the Rice PDF $p_{y\hspace{0.05cm}|\hspace{0.05cm}m} (\eta\hspace{0.05cm}|\hspace{0.05cm}m_0)$ and the Rayleigh PDF $p_{y\hspace{0.05cm}|\hspace{0.05cm}m} (\eta\hspace{0.05cm}|\hspace{0.05cm}m_1)$, this probability can only be determined numerically. The optimal decision boundary $G$ has to be determined beforehand as the solution of the following equation:
- \[p_{y\hspace{0.05cm}\vert \hspace{0.05cm}m} (G \hspace{0.05cm}|\hspace{0.05cm}m_0) = p_{y\hspace{0.05cm}|\hspace{0.05cm}m} (G \hspace{0.05cm}|\hspace{0.05cm}m_1) \hspace{0.05cm}.\]
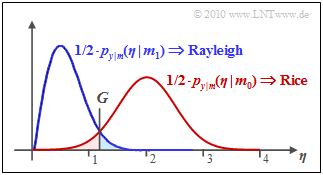
$\text{Example 1:}$ The graph shows the result of this equation for $\sigma_n = 0.5$ and $C = 2$, where the (red) Rice PDF is approximated by a Gaussian PDF with mean $C$ and standard deviation $\sigma_n$. One can see from this:
- The optimal decision boundary $($here: $G \approx 1.25)$ results from the intersection of the two curves.
- The symbol error probability $p_{\rm S}$ is the sum of the two colored areas. In the example, $p_{\rm S} \approx 5\%$ results.
You can determine the error probability for other values of $C$ and $\sigma_n$ as well as the optimal decision boundary $G$ using the calculation tool "Non-coherent On-Off Keying".
Non-coherent demodulation of binary FSK (2–FSK)
As already shown in the "last chapter", Binary Frequency Shift Keying (2–FSK) in the equivalent low-pass range can be described by the basis functions
- \[\xi_1(t) = \sqrt{1/T} \cdot {\rm e}^{\hspace{0.05cm}+{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} \pi \hspace{0.03cm}\cdot \hspace{0.03cm} h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},\]
- \[ \xi_2(t) = \sqrt{1/T} \cdot {\rm e}^{\hspace{0.05cm}-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} \pi \hspace{0.03cm}\cdot \hspace{0.03cm} h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T \hspace{0.05cm}\]
To achieve orthogonality between these two complex basis functions, the "modulation index" $h$ must be chosen to be integer:
- \[< \hspace{-0.05cm}\xi_1(t) \hspace{0.1cm} \cdot \hspace{0.1cm} \xi_2(t) \hspace{-0.05cm}> \hspace{0.2cm}= 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} h = 2 \cdot \Delta f_{\rm A} \cdot T\hspace{0.05cm}= 1, 2, 3, \text{...}\]
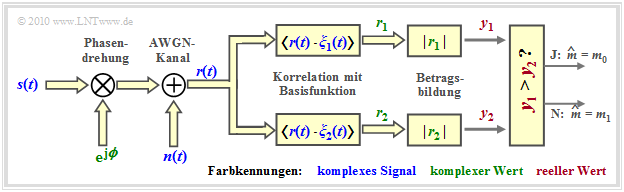
The diagram shows the structure for non-coherent orthogonal demodulation of binary FSK.
In the noise-free case ⇒ $n(t) \equiv 0$ applies to the outputs of the two correlators:
- \[r_1 = \hspace{0.2cm} < \hspace{-0.05cm}r(t) \hspace{0.1cm} \cdot \hspace{0.1cm} \xi_1(t) \hspace{-0.05cm}> \hspace{0.2cm}= 0\hspace{0.05cm}, \hspace{0.2cm} {\rm falls}\hspace{0.15cm} m = m_1\hspace{0.05cm},\]
- \[ r_2 = \hspace{0.2cm} < \hspace{-0.05cm}r(t) \hspace{0.1cm} \cdot \hspace{0.1cm} \xi_2(t) \hspace{-0.05cm}> \hspace{0.2cm}= 0\hspace{0.05cm}, \hspace{0.2cm} {\rm falls}\hspace{0.15cm} m = m_0\hspace{0.05cm}.\]
After respective amount formation ⇒ $y_1 = |r_1|, \ \ y_2 = |r_2|$ the following decision rule is then applicable:
- \[\hat{m} = \left\{ \begin{array}{c} m_0 \\ m_1 \end{array} \right.\quad \begin{array}{*{1}c} {\rm if}\hspace{0.15cm} y_1 > y_2 \hspace{0.05cm}, \\ {\rm if}\hspace{0.15cm} y_1 < y_2 \hspace{0.05cm}.\\ \end{array}\]
For a simpler realization of the decision, the difference $y_1 - y_2$ can also be evaluated with the decision boundary $G = 0$.
Error probability with non-coherent 2–FSK demodulation
In the following, the error probability is calculated under the assumption that $m = m_0$ was sent. Under the further assumption of equally probable binary messages $m_0$ and $m_1$, the absolute error probability is exactly the same:
- $${\rm Pr}({\cal{E}}) = {\rm Pr}({\cal{E}}\hspace{0.05cm} | \hspace{0.05cm}m_0) \hspace{0.05cm}.$$
With $m = m_0$ we get for the complex correlation output values $r_i$ and their amounts $y_i$:
- \[r_1 = \sqrt{E} \cdot {\rm e}^{{\rm j}\phi} + n_1\hspace{0.3cm} \Rightarrow \hspace{0.3cm}y_1 = |r_1|\hspace{0.15cm}{\rm is}\hspace{0.15cm}{\rm Rice}\hspace{0.15cm}{\rm distributed} \hspace{0.05cm},\]
- \[ r_2 = n_2\hspace{0.3cm} \Rightarrow \hspace{0.3cm}y_2 = |r_2|\hspace{0.15cm}{\rm is}\hspace{0.15cm}{\rm Rayleigh}\hspace{0.15cm}{\rm distributed} \hspace{0.05cm}.\]
Here, $E$ due to $M = 2$ represents the symbol energy $(E_{\rm S})$ and the bit energy $(E_{\rm B})$ equally, and $n_1$ and $n_2$ are uncorrelated complex noise variables with mean zero and variance $2 \cdot \sigma_n^2$. Thus, the "joint probability density function" is:
- \[p_{y_1,\hspace{0.03cm} y_2 \hspace{0.03cm}| \hspace{0.03cm}m} ( \eta_1, \eta_2 \hspace{0.05cm}| \hspace{0.05cm}m_0) = p_{y_1 \hspace{0.01cm}| \hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm}| \hspace{0.05cm}m_0) \cdot p_{y_2 \hspace{0.03cm}| \hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm}| \hspace{0.05cm}m_0) \hspace{0.05cm},\]
- \[\Rightarrow \hspace{0.5cm} p_{y_1 \hspace{0.01cm}| \hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm}| \hspace{0.05cm}m_0) = {\eta_1}/{\sigma_n^2} \cdot {\rm e }^{ - ({\eta_1^2 + E})/({2 \sigma_n^2}) }\cdot {\rm I }_0 \left [{\eta_1 \cdot \sqrt{E}}/{ \sigma_n^2}\right ] \hspace{0.05cm}, \hspace{0.5cm} p_{y_2 \hspace{0.01cm}| \hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm}| \hspace{0.05cm}m_0) = {\eta_2}/{\sigma_n^2} \cdot {\rm e }^{ - \eta_2^2 /({2 \sigma_n^2}) } \hspace{0.05cm}.\]
The error probability is generally obtained as follows:
- \[{\rm Pr}({\cal{E}}) = \int_{0}^{\infty} \int_{\eta_1}^{\infty} p_{y_1,\hspace{0.03cm} y_2 \hspace{0.03cm}| \hspace{0.03cm}m} ( \eta_1, \eta_2 \hspace{0.05cm}| \hspace{0.05cm}m_0) \,\,{\rm d} \eta_2\,\,{\rm d} \eta_1 = \int_{0}^{\infty} p_{y_1 \hspace{0.01cm}| \hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm}| \hspace{0.05cm}m_0) \cdot \int_{\eta_1}^{\infty} p_{y_2 \hspace{0.03cm}| \hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm}| \hspace{0.05cm}m_0)\,\,{\rm d} \eta_2\,\,{\rm d} \eta_1 \hspace{0.05cm}.\]
$\text{Conclusion:}$ For the error probability with non-coherent demodulation of the binary FSK, one obtains after some mathematical transformations the surprisingly simple result
- \[p_{\rm S} = {\rm Pr}({\cal{E} }) = {1}/{2} \cdot {\rm e}^{-E_{\rm S}/(2 N_0)} \hspace{0.05cm}.\]
For comparison, the result for coherent demodulation is given again:
- \[p_{\rm S} = {\rm Pr}({\cal{E} }) = {\rm Q}(\sqrt{ E_{\rm S}/N_0}) \hspace{0.05cm}.\]
$\text{Derivation:}$ The result taken in advance is now to be derived in some calculation steps. We start from the following equations:
- $${\rm Pr}({\cal{E} }) = \int_{0}^{\infty} p_{y_1 \hspace{0.01cm} \vert\hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm} \vert \hspace{0.05cm}m_0) \cdot \int_{\eta_1}^{\infty} p_{y_2 \hspace{0.03cm}\vert \hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm}\vert \hspace{0.05cm}m_0)\,\,{\rm d} \eta_2\,\,{\rm d} \eta_1 \hspace{0.05cm},\hspace{0.5cm}\text{with}$$
- $$p_{y_1 \hspace{0.01cm}\vert \hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm}\vert \hspace{0.05cm}m_0) = {\eta_1}/{\sigma_n^2} \cdot {\rm e }^{ - ({\eta_1^2 + E})/({2 \sigma_n^2}) }\cdot {\rm I }_0 \left [{\eta_1 \cdot \sqrt{E} }/{ \sigma_n^2}\right ] \hspace{0.05cm},\hspace{0.5cm}p_{y_\hspace{0.01cm}\vert \hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm}\vert \hspace{0.05cm}m_0) = {\eta_2}/{\sigma_n^2} \cdot {\rm e }^{ - \eta_2^2 /({2 \sigma_n^2}) } \hspace{0.05cm}.$$
(1) The inner integral gives the probability that the Rayleigh distributed random variable $\eta_2$ is larger than $\eta_1$ – see solution to "Exercise 4.17Z":
- $$\int_{\eta_1}^{\infty} p_{y_2 \hspace{0.03cm}\vert\hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm}\vert \hspace{0.05cm}m_0)\,\,{\rm d} \eta_2 = {\rm e }^{ - \eta_1^2 /({2 \sigma_n^2}) } \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Pr}({\cal{E} }) = \int_{0}^{\infty}{\eta_1}/{\sigma_n^2} \cdot {\rm e }^{ - ({2\eta_1^2 + E})/({2 \sigma_n^2}) }\cdot {\rm I }_0 \left [ {\eta_1 \cdot \sqrt{E} }/{ \sigma_n^2}\right ]\,\,{\rm d} \eta_1 \hspace{0.05cm}.$$
(2) With the (arbitrary) substitutions $C_0^2 = E/4$ and $\sigma_0^2 = \sigma_n^2/2$, we obtain:
- $${\rm Pr}({\cal{E} }) = \int_{0}^{\infty} \frac{\eta_1}{2 \cdot \sigma_0^2} \cdot {\rm exp } \left [ - \frac{2 \eta_1^2 + 4 C_0^2}{4 \sigma_0^2}\right ] \cdot {\rm I }_0 \left [ \frac{\eta_1 \cdot 2C_0}{ 2 \sigma_0^2}\right ]\,\,{\rm d} \eta_1 = \int_{0}^{\infty} \frac{\eta_1}{2 \cdot \sigma_0^2} \cdot {\rm exp } \left [ - \frac{\eta_1^2 + 2 C_0^2}{2 \sigma_0^2}\right ] \cdot {\rm I }_0 \left [ \frac{\eta_1 \cdot C_0}{ \sigma_0^2}\right ]\,\,{\rm d} \eta_1 \hspace{0.05cm}.$$
(3) By shifting fractions in front of the integral, we succeed that the integrand again describes a "Rice distribution":
- \[{\rm Pr}({\cal{E} }) = {1}/{2} \cdot {\rm exp } \left [ - \frac{ C_0^2}{2 \sigma_0^2}\right ] \cdot \int\limits_{0}^{\infty} \frac{\eta_1}{ \sigma_0^2} \cdot {\rm exp } \left [ - \frac{\eta_1^2 + C_0^2}{2 \sigma_0^2}\right ] \cdot {\rm I }_0 \left [ \frac{\eta_1 \cdot C_0}{ \sigma_0^2}\right ]\,\,{\rm d} \eta_1 \hspace{0.05cm}.\]
(4) The integrand now describes the Rice PDF. The integral over the entire definition area from $0$ to $+\infty$ yields the value one, as for any PDF, so that holds:
- \[{\rm Pr}({\cal{E} }) = {1}/{2} \cdot {\rm exp } \left [ - \frac{ C_0^2}{2 \sigma_0^2}\right ]\hspace{0.05cm}.\]
(5) Finally, with $C_0^2 = E/4$ and $\sigma_0^2 = \sigma_n^2/2$ and the generally valid relation $\sigma_n^2 = N_0$, we obtain:
- $${\rm Pr}({\cal{E} }) = {1}/{2} \cdot {\rm exp } \left [ - \frac{ C_0^2}{2 \sigma_0^2}\right ] = {1}/{2} \cdot {\rm exp } \left [ - \frac{ E_{\rm S}/4}{N_{\rm 0}/2}\right ] \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm S} = {\rm Pr}({\cal{E} }) = {1}/{2} \cdot {\rm e}^{-E_{\rm S}/(2 N_0)}\hspace{0.05cm}.$$
q.e.d. $E_{\rm S}$ here indicates the average signal energy per symbol, which is equal to the normalization energy $E$ for FSK.
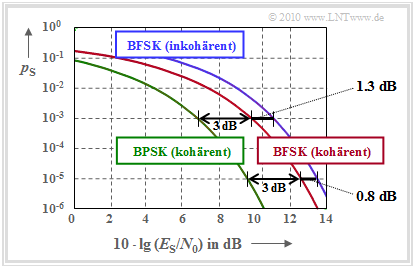
$\text{Example 2:}$ The graph compares the error probability curves of both demodulation methods as a function of the AWGN quotient $E_{\rm S}/N_0$.
One can see:
- The non-coherent FSK (red curve) requires a $0.8 \ \rm dB$ larger $E_{\rm S}/N_0$ compared to the coherent FSK (blue curve) at $p_{\rm S}= 10^{-5}$.
- At $p_{\rm S}= 10^{-3}$ the distance is even $1.3 \ \rm dB$.
- In contrast, the distance between the coherent binary FSK from the coherent BPSK is always $1.3 \ \rm dB$ regardless of the error probability.
Non-coherent demodulation of multi-level FSK
We now consider the message set $\{m_1, m_2,\hspace{0.05cm}\text{ ...} \hspace{0.05cm}, m_{M}\}$ and denote $M$ as the number of levels.
- As in the case of binary FSK, a prerequisite for the application of the modulation process "Frequency Shift Keying" and at the same time of a non-coherent demodulator is an integer modulation index $h$.
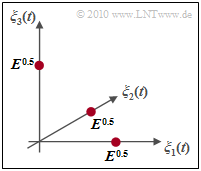
- In this case, the $M$–level FSK is orthogonal and a signal space constellation results as shown in the adjacent diagram for the special case $M = 3$.
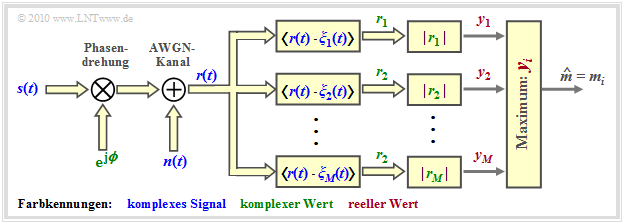
The non-coherent demodulator is sketched below. Compared to the "receiver structure for binary FSK", this receiver differs only by $M$ branches instead of only two, which provide the comparison values $y_1$, $y_2$, ... , $y_M$.
To calculate the error probability, we assume that $m_1$ was sent. This means that the decision is correct if the largest detection output value is $y_1$:
- \[{\rm Pr}({\cal{C}}) \hspace{-0.1cm} = \hspace{-0.1cm} {\rm Pr} \big [ (y_2 < y_1) \cap (y_3 < y_1) \cap ... \cap (y_{M} < y_1) \hspace{0.05cm}| \hspace{0.05cm} m = m_1\big ] = {\rm Pr} \left [ \hspace{0.1cm} \bigcap\limits_{k = 2}^M (y_k < y_1) \hspace{0.05cm}| \hspace{0.05cm}m = m_1\right ] \hspace{0.01cm}.\]
$\text{Conclusion:}$
- The error probability of M–level FSK in non-coherent demodulation is equal to ${\rm Pr}({\cal{E} }) = 1 - {\rm Pr}({\cal{C} })$.
- In the following, it is shown that ${\rm Pr}({\cal{C} })$ can be represented as follows:
- \[{\rm Pr}({\cal{C} }) = \sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot \frac{1}{i+1} \cdot {\rm exp } \left [ - \frac{i \cdot E_{\rm S} } {(i+1) \cdot N_0}\right ] \hspace{0.05cm}\hspace{0.5cm} \text{with}\hspace{0.5cm} E_{\rm S} = E_{\rm B} \cdot {\rm log_2}(M)\hspace{0.05cm}.\]
- In the special case $M = 2$, of course, the result obtained in the "last section" is again obtained:
- \[p_{\rm S} = {\rm Pr}({\cal{E} }) = {1}/{2} \cdot {\rm e}^{-E_{\rm S}/(2 N_0)} \hspace{0.05cm}.\]
$\text{Derivation:}$ The result taken in advance shall now be derived in some calculation steps. We assume that $m_1$ has been sent. This means that the decision is correct if the largest detection output value is $y_1$. Otherwise, there are certain analogies to the derivation of the "BFSK error probability".
(1) Using the conditional probability density $p_{y_1 \hspace{0.01cm} \vert\hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm} \vert \hspace{0.05cm}m_1)$, we obtain:
- \[{\rm Pr}({\cal{C} }) = \int_{0}^{\infty} {\rm Pr} \left [ \hspace{0.1cm} \bigcap\limits_{k = 2}^M (y_k < y_1) \hspace{0.05cm}\vert\hspace{0.05cm}y_1 = \eta_1, m = m_1\right ] \cdot p_{y_1 \hspace{0.01cm} \vert\hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm} \vert \hspace{0.05cm}m_1) \,\,{\rm d} \eta_1 \hspace{0.05cm}.\]
(2) The decision values $y_2$, $y_3$, ... , $y_M$ are statistically independent for given $y_1$. Therefore:
- \[{\rm Pr}({\cal{C} }) = \int_{0}^{\infty} \left \{ {\rm Pr} \big [ (y_2 < y_1) \hspace{0.05cm}\vert \hspace{0.05cm}y_1 = \eta_1, m = m_1\big ] \right \}^{M-1} \cdot p_{y_1 \hspace{0.01cm} \vert\hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm} \vert \hspace{0.05cm}m_1) \,\,{\rm d} \eta_1 \hspace{0.05cm}.\]
(3) The selected value $y_2$ conditioned on $m_1$ has a Rayleigh distribution with parameter $\sigma_n^2$:
- \[{\rm Pr} \big [ (y_2 < y_1) \hspace{0.05cm} \vert \hspace{0.05cm}y_1 = \eta_1, m = m_1\big ] \hspace{-0.1cm} = \hspace{-0.1cm} \int_{0}^{\eta_1} p_{y_2 \hspace{0.01cm} \vert\hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm} \vert \hspace{0.05cm}m_1)\,\,{\rm d} \eta_2= 1 - {\rm exp } \big [ - {\eta_1^2 }/({2 \sigma_n^2})\big ] = 1 - a \hspace{0.2cm}{\rm(abbreviation)} \hspace{0.05cm}.\]
(4) Now we are looking for the expression $(1 -a)^{M-1}$, for which with the abbreviation from (3) holds:
- \[ (1-a)^{M-1} \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot (-1)^i \cdot a^i = \sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot {\rm exp } \left [ - \frac{i \cdot \eta_1^2 }{2 \sigma_n^2}\right ] \hspace{0.05cm}.\]
(5) $y_1$ has a "Rice distribution" conditioned on $m=m_1$. Thus, the probability of a correct decision can be expressed in the following form:
- \[{\rm Pr}({\cal{C} }) \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot \int_{0}^{\infty} {\rm exp } \left [ - \frac{i \cdot \eta_1^2 }{2 \sigma_n^2}\right ] \cdot \frac{\eta_1}{ \sigma_n^2}\cdot {\rm exp } \left [ - \frac{\eta_1^2 + E_{\rm S} }{2 \sigma_n^2}\right ] \cdot {\rm I }_0 \left [ \frac{\eta_1 \cdot \sqrt{E_{\rm S} } }{ \sigma_n^2}\right ] \,\,{\rm d} \eta_1 \hspace{0.05cm}.\]
(6) Substitutions succeed in shaping the integrand according to the Rice distribution. Since each probability density integrates to one, we obtain:
- \[{\rm Pr}({\cal{C} }) = \sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot \frac{1}{i+1} \cdot {\rm exp } \left [ - \frac{i \cdot E_{\rm S} } {(i+1) \cdot N_0}\right ] \hspace{0.05cm}\hspace{0.5cm} \text{with}\hspace{0.5cm} E_{\rm S} = E_{\rm B} \cdot {\rm log_2}(M)\hspace{0.05cm}.\]
(7) The special case $M = 2$ leads to exactly the same result as calculated for the binary FSK:
- \[{\rm Pr}({\cal{C} }) = (-1)^0 \cdot {2-1 \choose 0 } \cdot \frac{1}{0+1} \cdot {\rm exp } \left [ - \frac{0 \cdot E_{\rm S} } {(i+1) \cdot N_0}\right ] + (-1)^1 \cdot {2-1 \choose 1 } \cdot \frac{1}{1+1} \cdot {\rm exp } \left [ - \frac{1 \cdot E_{\rm S} } {(i+1) \cdot N_0}\right ] \]
- \[ \Rightarrow \hspace{0.5cm} {\rm Pr}({\cal{C} }) = 1 - {1}/{2} \cdot {\rm e }^{-E_{\rm S}/(2N_0)} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} {\rm Pr}({\cal{E} }) = 1 - {\rm Pr}({\cal{C} }) = {1}/{2} \cdot {\rm e }^{-E_{\rm S}/(2N_0)} \hspace{0.05cm}.\]
Exercises for the chapter
Exercise 4.17: Non-Coherent On-Off Keying
Exercise 4.17Z: Rayleigh and Rice Distribution
Exercise 4.18: Non-Coherent FSK Demodulation
Exercise 4.18Z: BER of Coherent and Non-Coherent FSK
Exercise 4.19: Orthogonal Multilevel FSK