Contents
Principle and block diagram
Decision Feedback Equalization (DFE) is a method of reducing intersymbol interference. In German-language literature, this is sometimes also referred to as Quantized Feedback (QR).
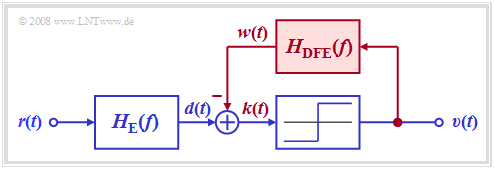
The graphic shows the corresponding receiver. It can be seen from the block diagram:
- Without the signal feedback shown in red, a conventional digital receiver with threshold equalizer would result according to the chapter "Ideal channel equalizer".
- For the following description, it is again assumed that the entire receiver filter $H_{\rm E}(f)$ is composed of the (fictitious) ideal channel equalizer $1/H_{\rm K}(f)$ and a Gaussian low-pass filter $H_{\rm G}(f)$ for noise power limitation.
- In the receiver with decision feedback, a compensation signal $w(t)$ is obtained from the rectangular output signal $v(t)$ via a linear network with the frequency response $H_{\rm DFE}(f)$ and fed back to the input of the threshold decision.
- This signal $w(t)$ is subtracted from the pre-equalized signal $d(t)$. If the feedback network is suitably dimensioned, the corrected signal $k(t) = d(t) - w(t)$ thus has no (or at least significantly fewer) pulse trailers than the signal $d(t)$. The pulse precursors, on the other hand, cannot be influenced for causality reasons.
- Since in this receiver with decision feedback the compensation signal $w(t)$ is derived from the noise-free sink signal $v(t)$, the signal equalization is not associated with an increase in noise power as in linear equalization. Rather, the corrected signal $k(t)$ has the same noise rms value $\sigma_d$ as the signal $d(t)$.
Notes:
(1) The signal characteristics of this nonlinear equalization method "DFE" as well as the associated error probabilities – valid for a distortion-free channel – can be displayed with the interactive applet "Decision feedback equalization".
(2) Further information on the topic as well as exercises, simulations and programming exercises can be found in the
- Experiment 3: Intersymbol interference and equalization, program "qrk"
- of the practical course "Simulation of digital transmission systems" [Söd01][1]. This (former) LNT course at the TU Munich is based on
- the teaching software package "LNTsim" ⇒ link refers to the ZIP version of the program and
- "this lab manual" ⇒ link refers to the PDF version (82 pages).
Ideal decision feedback
We first discuss the ideal DFE realization based on the basic pulses.
$\text{Definition:}$ Ideal decision feedback exists when the following basic pulse is applied to the decision:
- $$g_k(t) = \left\{ \begin{array}{c} g_d(t) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} \text{for} \\ \text{for} \\ \end{array} \begin{array}{*{20}c} t < T_{\rm D} + T_{\rm V}, \\ t \ge T_{\rm D} + T_{\rm V}. \\ \end{array}$$
This means that in the ideal case the basic compensation pulse $g_w(t)$ must exactly reproduce the linearly pre-equalized pulse $g_d(t)$ for all times $t > T_{\rm D} + T_{\rm V}$. The delay time $T_{\rm V}$ required for realization reasons must be smaller than the symbol duration $T$; in the following $T_{\rm V} = T/2$ always applies.
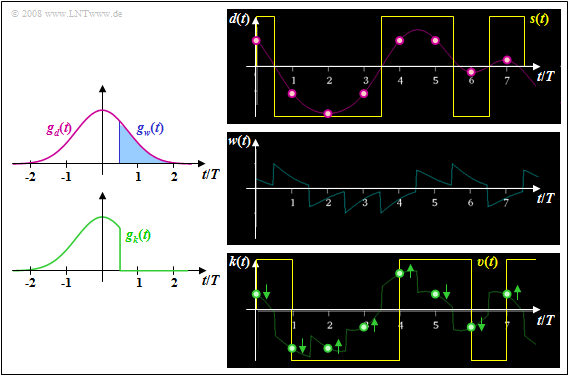
$\text{Example 1:}$ Let the total frequency response $H_{\rm K}(f) \cdot H_{\rm E}(f) = H_{\rm G}(f)$ be Gaussian with the cutoff frequency $f_{\rm G} = 0.3/T$. For NRZ rectangular pulses, this then yields the basic transmitter pulse $g_d(t)$ sketched in pink.
Shown on the left are the basic pulses $g_w(t)$ and $g_k(t)$ with ideal decision feedback, based on the detection time $T_{\rm D} = 0$ and the delay time $T_{\rm V} = T/2$.
The right pictures from [Söd01][1] – all without consideration of the noise – make clear that by the compensation of all pulse trailers by means of the correction signal $w(t)$ the distances of the useful distance values $d_{\rm S}(\nu \cdot T)$ from the decision threshold $E = 0$ are changed.
- Particularly small distances, such as at times $t = 6T$ and $t = 7T$, are significantly increased and thus their error probabilities are greatly reduced (arrows pointing away from the threshold).
- In contrast, the detection samples further away from the threshold value $E = 0$ in the signal $d(t)$ are shifted towards the threshold and their falsification probabilities are thus slightly increased. This can be seen, for example, for time $t = 5T$.
Eye opening and error probability with DFE
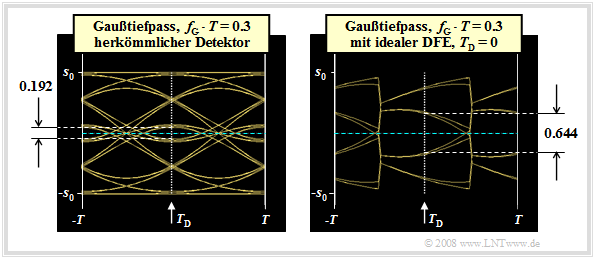
We now consider the eye diagrams without DFE (left graph) and with ideal DFE (right graph). We assume the same conditions as in the last section, so that the following basic pulse values are present:
- $$g_0 = g_d(t=0) = 0.548 \cdot s_0 \hspace{0.05cm},\hspace{0.2cm}g_1 = g_d(t=T) = 0.214 \cdot s_0 = g_{-1} \hspace{0.05cm}, \hspace{0.2cm}g_2 = g_d(t=2\hspace{0.05cm}T) = 0.012 \cdot s_0 = g_{-2} \hspace{0.05cm},\hspace{0.2cm}g_3 = g_{-3} = \text{...} \approx 0 \hspace{0.05cm}.$$
These two eye diagrams can be interpreted as follows:
- For the conventional receiver (without DFE), with binary bipolar redundancy-free coding considering symmetry:
- $${\ddot{o}(T_{\rm D} = 0 )} = {2} \cdot \big [ g_0 - | g_{-1}| - | g_{-2}| - | g_{1}| - | g_{2}|\big ] = {2} \cdot \big [ g_0 - 2 \cdot g_{1} - 2 \cdot g_{2}\big ]= 0.192 \cdot s_0 \hspace{0.05cm}.$$
- On the other hand, for ideal DFE, the two trailers $g_1$ and $g_2$ are fully compensated and we obtain for the vertical eye opening:
- $${\ddot{o}(T_{\rm D} = 0 )} = {2} \cdot \big [ g_0 - | g_{-1}| - |g_{-2}|\big ] = {2} \cdot \big [ g_0 - g_{1} - g_{2}\big ]= 0.644 \cdot s_0 \hspace{0.05cm}.$$
- Since the correction signal $w(t)$ is derived from the decision and thus noise-free signal $v(t)$, the noise rms value $\sigma_d$ is not changed by the decision feedback. Thus, the noise rms gain due to the DFE is equal to in the considered example
- $$G_{\rm DFE}= 20 \cdot {\rm lg}\hspace{0.1cm}\frac{0.644}{0.192} \approx 10.5\,{\rm dB} \hspace{0.05cm}.$$
$\text{Conclusion:}$ For a coaxial cable with characteristic cable attenuation $a_\star = 80 \ \rm dB$ and $10 \cdot \lg \ (E_{\rm B}/N_0) = 80 \ \rm dB$, for example, this signal-to-noise ratio gain means that the worst-case error probability $p_{\rm U}$ is reduced by DFE from $7\%$ to about $4 \cdot 10^{-7}$ – a quite remarkable improvement.
Optimization of a transmission system with DFE
The last section has already made clear that the DFE already causes an enormous gain in the signal-to-noise ratio if
- of a fixed cutoff frequency $f_{\rm G}$ and
- the fixed detection time $T_{\rm D} = 0$
is assumed. However, the system can be further improved if the two parameters $f_{\rm G}$ and $T_{\rm D}$ are optimized together.
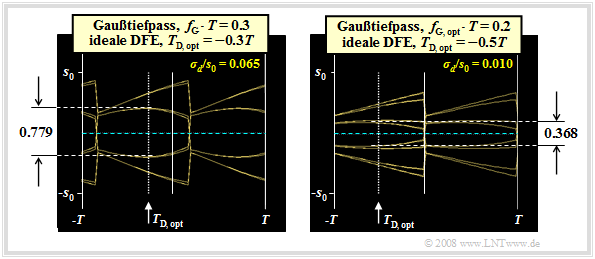
The graph shows the eye diagrams without noise for
- $f_{\rm G} \cdot T = 0.3$ (left) and
- $f_{\rm G} \cdot T = 0.2$ (right).
For the diagram and the following calculations, the characteristic cable attenuation $a_\star = 80 \ \rm dB$ and the AWGN parameter $10 \cdot \lg \ (E_{\rm B}/N_0) = 80 \ \rm dB$ (with $E_{\rm B} = s_0^2 \cdot T$) are still assumed.
The left diagram is largely identical – except for the detection time $T_{\rm D}$ – to the right eye diagram in the last section.
The optimization results can be summarized as follows:
- With $f_{\rm G} \cdot T = 0.3$, by shifting the detection time to $T_\text{D, opt} = -0.3T$, the eye opening can be increased to $\ddot{o}(T_\text{D, opt}) = 0.779 \cdot s_0 $.
- Compared to $T_{\rm D} = 0$ (compare last section), this results in a further gain of $G_{T_\text{D, opt}}= 20 \cdot {\rm lg}\hspace{0.1cm}{0.779}/{644} \approx 1.65\,{\rm dB} \hspace{0.05cm}.$
- The error probability is now found to be $p_{\rm U} \approx 1.3 \cdot 10^{-9}$ (versus $4 \cdot 10^{-7}$).
Beim DFE–Empfänger kann man aber zusätzlich die Grenzfrequenz weiter herabsetzen. Der Grund ist das bessere Rauschverhalten bei kleinerer Grenzfrequenz. Der normierte Rauscheffektivwert ergibt sich statt zu $\sigma_d/s_0 = 0.065$ $($für $f_{\rm G} \cdot T = 0.3)$ zum Beispiel zu $\sigma_d/s_0 = 0.010$ $($für $f_{\rm G} \cdot T = 0.2)$.
- So ergibt sich mit $f_{\rm G} \cdot T = 0.2$ und $T_{\rm D} = 0$ die zwar kleine, aber immerhin von Null verschiedene Augenöffnung $\ddot{o}_{\rm norm} = 0.152$, die zusammen mit dem sehr günstigen Rauscheffektivwert zum (ungünstigsten) Störabstand $17.6 \ \rm dB$ und zur (ungünstigsten) Fehlerwahrscheinlichkeit $p_{\rm U} \approx 1.6 \cdot 10^{-14}$ führt.
- Durch Kombination der Grenzfrequenz $f_{\rm G} \cdot T = 0.2$ mit dem Detektionszeitpunkt $T_{\rm D} = -T/2$ erhält man schließlich die bei den getroffenen Voraussetzungen optimale Systemkonfiguration mit der normierten Augenöffnung $\ddot{o}_{\rm norm} = 0.368$ und dem (ungünstigsten) Störabstand $10 \cdot \lg \ \rho_{\rm U} = 25.3 \ \rm dB$.
- Die Fehlerwahrscheinlichkeit ist damit (praktisch) Null. Praxisrelevant ist allerdings diese Konfiguration nicht: Bereits eine minimale Toleranz der Systemparameter führt schon zu einem geschlossenem Auge.
Realisierungsaspekte der Entscheidungsrückkopplung
Als ein wesentliches Ergebnis des letzten Kapitels Lineare Nyquistentzerrung und des aktuellen Kapitels "Entscheidungsrückkopplung" empfiehlt sich folgende Vorgehensweise:
$\text{Fazit:}$ Für ein Übertragungssystem über Kupferleitungen (Koaxialkabel, Zweidrahtleitung) sind aufgrund des erreichbaren Signal–zu–Rauschabstandes am Entscheider folgende Systemvarianten besonders geeignet:
- ein Mehrstufensystem $($zum Beispiel $M = 4)$ und die optimale Nyquistentzerrung zur Kompensation der starken Impulsinterferenzen, hervorgerufen durch die linearen Kanalverzerrungen;
- ein Binärsystem mit relativ kleiner Bandbreite des Gesamtfrequenzganges $H_{\rm G}(f) = H_{\rm K}(f) \cdot H_{\rm E}(f)$ und ein nichtlinearer Detektor mit DFE.
Beide Systemvarianten liefern bei idealisierten Bedingungen vergleichbar gute Resultate. Zu beachten ist allerdings, dass es durch Realisierungsungenauigkeiten bei beiden Systemen zu großen Degradationen kommen kann, die hier am Beispiel des DFE–Systems genannt werden:
- Da über das Fernsprechnetz kein Gleichsignal übertragen werden kann, für unsere Berechnungen aber $H_{\rm K}(f=0) = 1$ angenommen wird, ist am Empfänger eine Gleichsignalwiedergewinnung erforderlich. Diese Aussage trifft in gleicher Weise für das quaternäre Nyquistsystem zu.
- Beim DFE–System muss der Kompensationsimpuls $g_w(t)$ den vorentzerrten Grundimpuls $g_d(t)$ exakt nachbilden. Dies ist insbesondere dann schwierig, wenn $g_d(t)$ sehr breit ist $($kleine Grenzfrequenz, zum Beispiel $f_{\rm G} \cdot T = 0.2)$ und die Optimierung den Detektionszeitpunkt $T_\text{D, opt} = -T/2$ liefert.
- Kommt es aufgrund eines sehr großen Rauschwertes zu einer Fehlentscheidung, so werden auch die nachfolgenden Symbole mit großer Wahrscheinlichkeit verfälscht. Allerdings gibt es immer wieder Symbolfolgen, die diese Fehlerfortpflanzung unterbrechen.
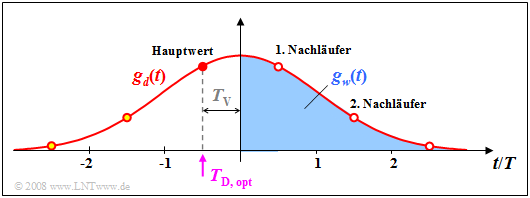
$\text{Beispiel 2:}$ Die Grafik zeigt den Grundimpuls $g_d(t)$
- für die Grenzfrequenz $f_{\rm G} \cdot T = 0.2$ (rote Kurve) und
- den Kompensationsimpuls $g_w(t)$ für $T_\text{D} = -T/2$ (blau gefüllt).
Hierbei ist eine Verzögerungszeit $T_\text{V} = -T/2$ zwischen Entscheidung und Beginn der Signalkorrektur berücksichtigt. Man erkennt:
- Für $T_\text{D} = -T/2$ ist der erste Nachläufer $g_d(T_\text{D} +T) = g_d(T/2)$ genau so groß wie der Hauptwert $g_d(T_\text{D}) = g_d(-T/2)$.
- Gelingt es nicht, alle Nachläufer vollständig zu kompensieren, so ergibt sich schnell ein geschlossenes Auge und damit im ungünstigsten Fall (Worst–Case) die Fehlerwahrscheinlichkeit $p_{\rm U} \approx 50\%$.
Entscheidungsrückkopplung mit Laufzeitfilter
Für eine schaltungstechnische Realisierung genügt es, wenn der korrigierte Grundimpuls $g_k(t)$ nur zu den äquidistanten Detektionszeitpunkten $T_\text{D} +\nu \cdot T$ zu Null wird.
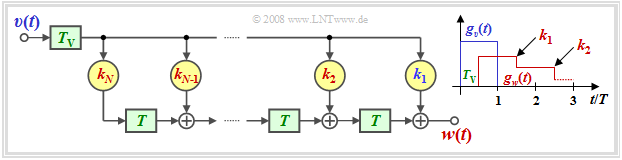
Eine Realisierungsmöglichkeit stellt somit ein unsymmetrisches Laufzeitfilter gemäß nebenstehender Grafik dar,
- dessen Ordnung $N$ (Anzahl der Filterkoeffizienten), und
- dessen Filterkoeffizienten $ k_\nu$ $($mit $\nu = 1$, ... , $N)$
durch den Grundimpuls $g_d(t)$ sowie den Detektionszeitpunkt $T_\text{D}$ festgelegt sind.
Diese DFE–Realisierung weist folgende Eigenschaften auf:
- Da das Ausgangssignal $v(t)$ rechteckförmig ist, ist der Kompensationsimpuls $g_w(t)$ treppenförmig.
- Bei richtiger Dimensionierung der Filterkoeffizienten $k_\nu$ gilt für $\nu = 1$, ... , $N$:
- $$g_w(T_{\rm D} + \nu \cdot T) = g_d(T_{\rm D} + \nu \cdot T) \hspace{0.3cm}\Rightarrow\hspace{0.3cm} g_k(T_{\rm D} + \nu \cdot T) = 0 \hspace{0.05cm}.$$
- Zum Detektionszeitpunkt $T_\text{D}$ ergibt sich die genau gleiche vertikale Augenöffnung wie bei idealer DFE. Nachteilig ist eine kleinere horizontale Augenöffnung.
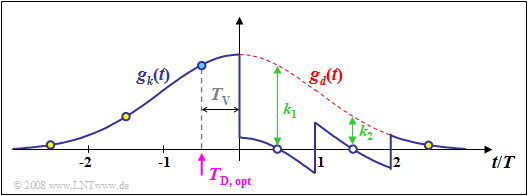
$\text{Beispiel 3:}$ Die Grafik zeigt die Grundimpulse $g_d(t)$ und $g_w(t)$ bei der Entscheidungsrückkopplung mit einem Laufzeitfilter zweiter Ordnung. Es gelten die gleichen Voraussetzungen wie für das $\text{Beispiel 2}$ auf der letzten Seite: $f_{\rm G} \cdot T = 0.2$ und $T_\text{D} = -T/2$. Man erkennt:
- Wegen der Ordnung $N = 2$ werden hier allerdings nur die beiden ersten Nachläufer $g_d(0.5T)$ und $g_d(1.5T)$ kompensiert.
- Der dritte Nachläufer $g_d(2.5T)$ könnte durch einen weiteren Filterkoeffizienten $k_3$ zu Null gemacht werden.
- Dagegen können die Impulsvorläufer $g_d(-1.5T)$ und $g_d(-2.5T)$ prinzipiell nicht kompensiert werden.
Aufgaben zum Kapitel
Aufgabe 3.8: Decision Feedback Equalization mit Laufzeitfilter
Aufgabe 3.8Z: Optimaler Detektionszeitpunkt bei DFE
Quellenverzeichnis