Difference between revisions of "Digital Signal Transmission/Parameters of Digital Channel Models"
| Line 109: | Line 109: | ||
*This inner block is characterized exclusively by its error sequence $ \langle e\hspace{0.05cm}'_\nu \rangle$, which refers to its input symbol sequence $ \langle c_\nu \rangle$ and output symbol sequence $ \langle w_\nu \rangle$. It is obvious that this channel model provides less information than a detailed analog model considering all components. | *This inner block is characterized exclusively by its error sequence $ \langle e\hspace{0.05cm}'_\nu \rangle$, which refers to its input symbol sequence $ \langle c_\nu \rangle$ and output symbol sequence $ \langle w_\nu \rangle$. It is obvious that this channel model provides less information than a detailed analog model considering all components. | ||
| − | * | + | *In contrast, the "outer" error sequence $ \langle e_\nu \rangle$ refers to the source symbol sequence $ \langle q_\nu \rangle$ and the sink symbol sequence $ \langle v_\nu \rangle$ and thus to the overall system including the specific encoding and the decoder on the receiver side.<br> |
| − | * | + | *The comparison of the two error sequences with and without consideration of encoder/decoder allows conclusions to be drawn about the efficiency of the underlying encoding and decoding. These two components are meaningful if and only if the outer comparator indicates fewer errors on average than the inner comparator.<br> |
| − | == | + | == Error sequence and average error probability == |
<br> | <br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ The transmission behavior of a binary system is completely described by the '''error sequence''' $ \langle e_\nu \rangle$: |
::<math>e_{\nu} = | ::<math>e_{\nu} = | ||
\left\{ \begin{array}{c} 1 \\ | \left\{ \begin{array}{c} 1 \\ | ||
0 \end{array} \right.\quad | 0 \end{array} \right.\quad | ||
| − | \begin{array}{*{1}c} {\rm | + | \begin{array}{*{1}c} {\rm if}\hspace{0.15cm}\upsilon_\nu \ne q_\nu \hspace{0.05cm}, |
\\ {\rm falls}\hspace{0.15cm} \upsilon_\nu = q_\nu \hspace{0.05cm}.\\ \end{array}</math> | \\ {\rm falls}\hspace{0.15cm} \upsilon_\nu = q_\nu \hspace{0.05cm}.\\ \end{array}</math> | ||
| − | + | From this, the (average) '''bit error probability''' can be calculated as follows: | |
::<math>p_{\rm M} = {\rm E}\big[e \big] = \lim_{N \rightarrow \infty} \frac{1}{N} | ::<math>p_{\rm M} = {\rm E}\big[e \big] = \lim_{N \rightarrow \infty} \frac{1}{N} | ||
\sum_{\nu = 1}^{N}e_{\nu}\hspace{0.05cm}.</math> | \sum_{\nu = 1}^{N}e_{\nu}\hspace{0.05cm}.</math> | ||
| − | + | It is assumed here that the random process generating the wrong decisions is [[Theory_of_Stochastic_Signals/Auto-Correlation_Function#Stationary_random_processes| "stationary"]] and [[Theory_of_Stochastic_Signals/Auto-Correlation_Function#Ergodic_random_processes|"ergodic"]], so that the error sequence $ \langle e_\nu \rangle$ can also be formally described completely by the random variable $e \in \{0, \ 1\}$. Thus, the transition from time to coulter averaging is allowed.}}<br> | |
| − | <i> | + | <i>Note:</i> In all other $\rm LNTwww $ books, the mean bit error probability is denoted by $p_{\rm B}$. To avoid confusion in connection with the [[Digital_Signal_Transmission/Burst_Error_Channels#Channel_model_according_to_Gilbert-Elliott|"Gilbert–Elliott model"]], this renaming here is unavoidable, and we will no longer refer to the bit error probability in the following, but only to the mean error probability $p_{\rm M}$.<br> |
| − | == | + | == Error correlation function == |
<br> | <br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ An important descriptive quantity of the digital channel models is also the die '''error correlation function''' – abbreviated ECF: |
::<math>\varphi_{e}(k) = {\rm E}\big [e_{\nu} \cdot e_{\nu + k}\big ] = \overline{e_{\nu} \cdot e_{\nu + k} }\hspace{0.05cm}.</math>}} | ::<math>\varphi_{e}(k) = {\rm E}\big [e_{\nu} \cdot e_{\nu + k}\big ] = \overline{e_{\nu} \cdot e_{\nu + k} }\hspace{0.05cm}.</math>}} | ||
| − | + | This has the following properties: | |
| − | *$\varphi_{e}(k) $ | + | *$\varphi_{e}(k) $ indicates the (discrete-time) [[Theory_of_Stochastic_Signals/Auto-Correlation_Function#Random_processes |"auto-correlation function]] of the random variable $e$, which is also discrete-time. The sweeping line in the right equation denotes the time averaging.<br> |
| − | * | + | *The error correlation value $\varphi_{e}(k) $ provides statistical information about two sequence elements that are $k$ apart, for example about $e_{\nu}$ and $e_{\nu+ k}$. The intervening elements $e_{\nu+ 1}$, ... , $e_{\nu+ k-1}$ do not affect the $\varphi_{e}(k)$ value.<br> |
| − | * | + | *For stationary sequences, regardless of the error statistic due to $e \in \{0, \ 1\}$, always holds: |
::<math>\varphi_{e}(k = 0) = {\rm E}\big[e_{\nu} \cdot e_{\nu}\big] = {\rm | ::<math>\varphi_{e}(k = 0) = {\rm E}\big[e_{\nu} \cdot e_{\nu}\big] = {\rm | ||
E}\big[e^2\big]= {\rm E}\big[e\big]= {\rm Pr}(e = 1)= p_{\rm M}\hspace{0.05cm},</math> | E}\big[e^2\big]= {\rm E}\big[e\big]= {\rm Pr}(e = 1)= p_{\rm M}\hspace{0.05cm},</math> | ||
| Line 152: | Line 152: | ||
{\rm E}\big[e_{\nu + k}\big] = p_{\rm M}^2\hspace{0.05cm}.</math> | {\rm E}\big[e_{\nu + k}\big] = p_{\rm M}^2\hspace{0.05cm}.</math> | ||
| − | * | + | *The error correlation function is an at least weakly decreasing function. The slower the decay of the ECF values, the longer the memory of the channel and the further the statistical ties of the error sequence.<br><br> |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 3:}$ In a binary transmission, $100$ of the total $N = 10^5$ transmitted binary symbols are falsified, so that the error sequence $ \langle e_\nu \rangle$ consists of $100$ ones and $99900$ zeros. |
| − | * | + | *Thus, the average error probability is $p_{\rm M} =10^{-3}$. |
| − | * | + | *The error correlation function $\varphi_{e}(k)$ starts at $p_{\rm M} =10^{-3}$ $($for $k = 0)$ and tends towards $p_{\rm M}^2 =10^{-6}$ $($für $k = \to \infty)$ for very large $k$ values. |
| − | * | + | *So far, no statement can be made about the actual course of $\varphi_{e}(k)$ with the information given here.}}<br> |
| − | == | + | == Relationship between error sequence and error distance == |
<br> | <br> | ||
| − | [[File:P ID1825 Dig T 5 1 S5 version1.png|right|frame| | + | [[File:P ID1825 Dig T 5 1 S5 version1.png|right|frame|For the definition of the error distance|class=fit]] |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ The '''error distance''' $a$ is the number of correctly transmitted symbols between two channel errors plus $1$. |
| − | + | The graphic illustrates this definition. | |
| − | * | + | *Any information about the transmission behavior of the digital channel contained in the error sequence $ \langle e_\nu \rangle$ is also contained in the sequence $ \langle a_n \rangle$ of error distances. |
| − | * | + | *Since the sequences $ \langle e_\nu \rangle$ and $ \langle a_n \rangle$ are not synchronous, we use different indices $(\nu$ and $n)$.}}<br> |
| − | + | In particular, we can see from the graph: | |
| − | * | + | *Since the first symbol was transmitted correctly $(e_1 = 0)$ and the second incorrectly $(e_2 = 1)$, the error distance is $a_1 = 2$.<br> |
| − | *$a_2 = 4$ | + | *$a_2 = 4$ indicates that three symbols were transmitted correctly between the first two errors $(e_2 = 1, \ e_5 = 1)$. <br> |
| − | * | + | *If two errors follow each other directly, the error distance is equal to $1$, like $a_3$ in the graphic above.<br> |
| − | * | + | *The event "$a = k$" means simultaneously $k-1$ error-free symbols between two errors. |
| − | * | + | *If an error occurred at time $\nu$, the next error follows at "$a = k$" exactly at time $\nu + k$.<br> |
| − | * | + | *The set of values of the random variable $a$ is the set of natural numbers in contrast to the binary random variable $e$: |
::<math>a \in \{ 1, 2, 3, ... \}\hspace{0.05cm}, \hspace{0.5cm}e \in \{ 0, 1 \}\hspace{0.05cm}.</math> | ::<math>a \in \{ 1, 2, 3, ... \}\hspace{0.05cm}, \hspace{0.5cm}e \in \{ 0, 1 \}\hspace{0.05cm}.</math> | ||
| − | * | + | *The average error probability can be determined from both random variables: |
::<math>{\rm E}\big[e \big] = {\rm Pr}(e = 1) =p_{\rm M}\hspace{0.05cm}, \hspace{0.5cm} {\rm E}\big[a \big] = \sum_{k = 1}^{\infty} k \cdot {\rm Pr}(a = k) = {1}/{p_{\rm M}}\hspace{0.05cm}.</math> | ::<math>{\rm E}\big[e \big] = {\rm Pr}(e = 1) =p_{\rm M}\hspace{0.05cm}, \hspace{0.5cm} {\rm E}\big[a \big] = \sum_{k = 1}^{\infty} k \cdot {\rm Pr}(a = k) = {1}/{p_{\rm M}}\hspace{0.05cm}.</math> | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 4:}$ In the sketched sequence $16$ of the total $N = 40$ symbols are falsified ⇒ $p_{\rm M} = 0.4$. Accordingly, the expected value of the error distances gives |
::<math>{\rm E}\big[a \big] = 1 \cdot {4}/{16}+ 2 \cdot {5}/{16}+ 3 \cdot {4}/{16}+4 \cdot {1}/{16}+5 \cdot {2}/{16}= 2.5 = | ::<math>{\rm E}\big[a \big] = 1 \cdot {4}/{16}+ 2 \cdot {5}/{16}+ 3 \cdot {4}/{16}+4 \cdot {1}/{16}+5 \cdot {2}/{16}= 2.5 = | ||
{1}/{p_{\rm M} }\hspace{0.05cm}.</math>}} | {1}/{p_{\rm M} }\hspace{0.05cm}.</math>}} | ||
| − | == | + | ==Error distance distribution == |
<br> | <br> | ||
| − | + | The [[Theory_of_Stochastic_Signals/Probability_Density_Function_(PDF)|"probability density function"]] (PDF) of the discrete random variable $a \in \{1, 2, 3, \text{...}\}$ is composed of an (infinite) sum of Dirac delta functions according to the chapter [[Theory_of_Stochastic_Signals/Probability_Density_Function_(PDF)#PDF_definition_for_discrete_random_variables|"PDF definition for discrete random variables"]] in the book "Stochastic Signal Theory": | |
::<math>f_a(a) = \sum_{k = 1}^{\infty} {\rm Pr}(a = k) \cdot \delta (a-k)\hspace{0.05cm}.</math> | ::<math>f_a(a) = \sum_{k = 1}^{\infty} {\rm Pr}(a = k) \cdot \delta (a-k)\hspace{0.05cm}.</math> | ||
| − | + | We refer to this particular PDF as the ''error distance density function''. Based on the error sequence, the probability that the error distance $a$ is exactly equal to $k$ can be expressed by the following conditional probability: | |
::<math>{\rm Pr}(a = k) = {\rm Pr}(e_{\nu + 1} = 0 \hspace{0.15cm}\cap \hspace{0.15cm} \text{...} \hspace{0.15cm}\cap \hspace{0.15cm}\hspace{0.05cm} | ::<math>{\rm Pr}(a = k) = {\rm Pr}(e_{\nu + 1} = 0 \hspace{0.15cm}\cap \hspace{0.15cm} \text{...} \hspace{0.15cm}\cap \hspace{0.15cm}\hspace{0.05cm} | ||
e_{\nu + k -1} = 0 \hspace{0.15cm}\cap \hspace{0.15cm}e_{\nu + k} = 1 \hspace{0.1cm}| \hspace{0.1cm} e_{\nu } = 1)\hspace{0.05cm}.</math> | e_{\nu + k -1} = 0 \hspace{0.15cm}\cap \hspace{0.15cm}e_{\nu + k} = 1 \hspace{0.1cm}| \hspace{0.1cm} e_{\nu } = 1)\hspace{0.05cm}.</math> | ||
| − | + | In the book "Stochastic Signal Theory" you will also find the definition of the [[Theory_of_Stochastic_Signals/Cumulative_Distribution_Function#CDF_for_discrete-valued_random_variables|"distribution function"]] of the discrete random variable $a$: | |
::<math>F_a(k) = {\rm Pr}(a \le k) \hspace{0.05cm}.</math> | ::<math>F_a(k) = {\rm Pr}(a \le k) \hspace{0.05cm}.</math> | ||
| − | + | This function is obtained from the PDF $f_a(a)$ by integration from $1$ to $k$. The function $F_a(k)$ can take values between $0$ and $1$ (including these two limits) and is weakly monotonically increasing.<br> | |
| − | + | In the context of digital channel models, the literature deviates from this usual definition. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ Rather, here the '''error distance distribution''' (EDD) gives the probability that the error distance $a$ is greater than or equal to $k$: |
::<math>V_a(k) = {\rm Pr}(a \ge k) = 1 - \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa)\hspace{0.05cm}.</math> | ::<math>V_a(k) = {\rm Pr}(a \ge k) = 1 - \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa)\hspace{0.05cm}.</math> | ||
| − | + | In particular: | |
:$$V_a(k = 1) = 1 \hspace{0.05cm},\hspace{0.5cm} \lim_{k \rightarrow \infty}V_a(k ) = | :$$V_a(k = 1) = 1 \hspace{0.05cm},\hspace{0.5cm} \lim_{k \rightarrow \infty}V_a(k ) = | ||
0 \hspace{0.05cm}.$$}} | 0 \hspace{0.05cm}.$$}} | ||
| − | + | The following relationship holds between the monotonically increasing function $F_a(k)$ and the monotonically decreasing function $V_a(k)$: | |
::<math>F_a(k ) = 1-V_a(k +1) \hspace{0.05cm}.</math> | ::<math>F_a(k ) = 1-V_a(k +1) \hspace{0.05cm}.</math> | ||
| − | [[File:P ID1826 Dig T 5 1 S5b version1.png|right|frame| | + | [[File:P ID1826 Dig T 5 1 S5b version1.png|right|frame|Discrete probability density and distribution functions|class=fit]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 5:}$ The graph shows in the left sketch an arbitrary discrete error distance density function $f_a(a)$ and the resulting <i>cumulative functions</i> |
| − | * $F_a(k ) = {\rm Pr}(a \le k)$ ⇒ | + | * $F_a(k ) = {\rm Pr}(a \le k)$ ⇒ middle sketch, as well as |
| − | * $V_a(k ) = {\rm Pr}(a \ge k)$ ⇒ | + | * $V_a(k ) = {\rm Pr}(a \ge k)$ ⇒ right sketch.<br> |
| − | + | For example, for $k = 2$, we obtain: | |
::<math>F_a( k =2 ) = {\rm Pr}(a = 1) + {\rm Pr}(a = 2) \hspace{0.05cm}, </math> | ::<math>F_a( k =2 ) = {\rm Pr}(a = 1) + {\rm Pr}(a = 2) \hspace{0.05cm}, </math> | ||
| Line 241: | Line 241: | ||
::<math>\Rightarrow \hspace{0.3cm} V_a(k =2 ) = 1-F_a(k = 1) = 0.6\hspace{0.05cm}.</math> | ::<math>\Rightarrow \hspace{0.3cm} V_a(k =2 ) = 1-F_a(k = 1) = 0.6\hspace{0.05cm}.</math> | ||
| − | + | For $k = 4$, the following results are obtained: | |
::<math>F_a(k = 4 ) = {\rm Pr}(a \le 4) = 1 | ::<math>F_a(k = 4 ) = {\rm Pr}(a \le 4) = 1 | ||
\hspace{0.05cm}, \hspace{0.5cm} V_a(k = 4 ) = {\rm Pr}(a \ge 4)= {\rm Pr}(a = 4) = 0.1 = 1-F_a(k = 3) | \hspace{0.05cm}, \hspace{0.5cm} V_a(k = 4 ) = {\rm Pr}(a \ge 4)= {\rm Pr}(a = 4) = 0.1 = 1-F_a(k = 3) | ||
\hspace{0.05cm}.</math>}}<br> | \hspace{0.05cm}.</math>}}<br> | ||
| − | == | + | ==Exercises for the chapter== |
<br> | <br> | ||
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_5.1:_Error_Distance_Distribution|Exercise 5.1: Error Distance Distribution]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_5.2:_Error_Correlation_Function|Exercise 5.2: Error Correlation Function]] |
{{Display}} | {{Display}} | ||
Revision as of 09:30, 19 August 2022
Contents
- 1 # OVERVIEW OF THE FIFTH MAIN CHAPTER #
- 2 Application of analog channel models
- 3 Definition of digital channel models
- 4 Example application of digital channel models
- 5 Error sequence and average error probability
- 6 Error correlation function
- 7 Relationship between error sequence and error distance
- 8 Error distance distribution
- 9 Exercises for the chapter
# OVERVIEW OF THE FIFTH MAIN CHAPTER #
At the end of the book "Digital Signal Transmission", digital channel models are discussed which do not describe the transmission behavior of a digital transmission system in great detail according to the individual system components, but rather globally on the basis of typical error structures. Such channel models are mainly used for cascaded transmission systems for the inner block, if the performance of the outer system components - for example, coder and decoder - is to be determined by simulation. The following are dealt with in detail:
- the descriptive variables error correlation function and error distance distribution,
- the BSC model (Binary Symmetric Channel ) for the description of statistically independent errors,
- the bundle error channel models according to Gilbert-Elliott and McCullough,
- the Wilhelm channel model for the formulaic approximation of measured error curves,
- some notes on the generation of fault sequences, for example with respect to error distance simulation,
- the effects of different error structures on BMP files ⇒ images and WAV files ⇒ audios.
Note: All BMP images and WAV audios of this chapter were generated with the Windows program "Digital Channel Models & Multimedia" from the (former) practical course "Simulation of Digital Transmission Systems " at the Chair of Communications Engineering of the TU Munich.
Application of analog channel models
For investigations of message transmission systems, suitable channel models are of great importance, because they are the
- prerequisite for system simulation and optimization, as well as
- creating consistent and reconstructible boundary conditions.
For digital signal transmission, there are both analog and digital channel models:
- Although an analog channel model does not have to reproduce the transmission channel in all physical details, it should describe its transmission behavior, including the dominant noise variables, with sufficient functional accuracy.
- In most cases, a compromise must be found between mathematical manageability and the relationship to reality.
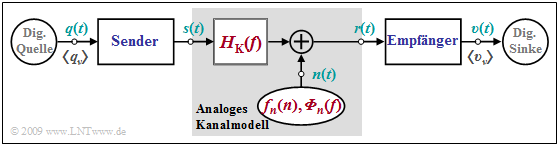
$\text{Example 1:}$ The graphic shows an analog channel model within a digital transmission system. This contains
- the "channel frequency response" $H_{\rm K}(f)$ to describe the linear distortions, and
- an additive noise signal $n(t)$, characterized by the "probability density function" (PDF) $f_n(n)$ and the "power-spectral density" (PSD) ${\it \Phi}_n(f)$.
A special case of this model is the so-called "AWGN channel" (Additive White Gaussian Noise) with the system properties
- \[H_{\rm K}(f) = 1\hspace{0.05cm},\hspace{0.2cm}{\it \Phi}_{n}(f) = {\rm const.}\hspace{0.05cm},\hspace{0.2cm} {f}_{n}(n) = \frac{1}{\sqrt{2 \pi} \cdot \sigma} \cdot {\rm e}^{-n^2\hspace{-0.05cm}/(2 \sigma^2)}\hspace{0.05cm}.\]
This simple model is suitable, for example, for describing a radio channel with time-invariant behavior, where the model is abstracted such that
- the actual band-pass channel is described in the equivalent low-pass range, and
- the attenuation, which depends on the frequency band and the transmission path length, is offset against the variance $\sigma^2$ of the noise signal $n(t)$.
To take time-variant characteristics into account, one must use other models such as "Rayleigh ading", "Rice fading" and "Lognormal fading",
which are described in the book "Mobile communications".
For wired transmission systems, the specific frequency response of the transmission medium according to the specifications for "coaxial cable" and "two-wire line" in the book "Linear Time-Invariant Systems" must be taken into account in particular, but also the fact that white noise can no longer be assumed due to "extraneous noise" (crosstalk, electromagnetic fields, etc.).
In the case of optical systems, the multiplicatively acting, i.e. signal-dependent "shot noise" must also be suitably incorporated into the analog channel model.
Definition of digital channel models
An analog channel model is characterized by analog input and output variables. In contrast, in a digital channel model (sometimes referred to as "discrete"), both the input and the output are discrete in time and value. In the following, let these be the source symbol sequence $ \langle q_\nu \rangle$ with $ q_\nu \in \{\rm L, \ H\}$ and the sink symbol sequence $ \langle v_\nu \rangle$ with $ v_\nu \in \{\rm L, \ H\}$. The indexing variable $\nu$ can take values between $1$ and $N$.
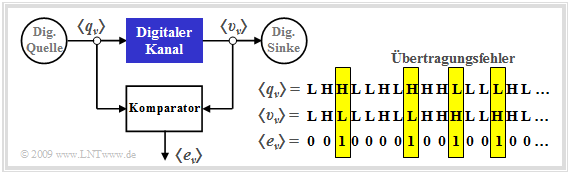
As a comparison with the "block diagram" in $\text{Example 1}$ shows, the "digital channel" is a simplifying model of the analog transmission channel including the technical transmission and reception units. Simplifying because this model only refers to the occurring transmission errors, represented by the error sequence $ \langle e_\nu \rangle$ with
- \[e_{\nu} = \left\{ \begin{array}{c} 1 \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm if}\hspace{0.15cm}\upsilon_\nu \ne q_\nu \hspace{0.05cm}, \\ {\rm if}\hspace{0.15cm} \upsilon_\nu = q_\nu \hspace{0.05cm}.\\ \end{array}\]
While $\rm L$ and $\rm H$ denote the possible symbols, which here stand for Low and High, $ e_\nu \in \{\rm 0, \ 1\}$ is a real number value. Often the symbols are also defined as $ q_\nu \in \{\rm 0, \ 1\}$ and $ v_\nu \in \{\rm 0, \ 1\}$. To avoid confusion, we have used the somewhat unusual nomenclature here.
The error sequence $ \langle e_\nu \rangle$ given in the graph
- is obtained by comparing the two binary sequences $ \langle q_\nu \rangle$ and $ \langle v_\nu \rangle$,
- contains only information about the sequence of transmission errors and thus less information than an analog channel model,
- is conveniently approximated by a random process with only a few parameters.
$\text{Conclusion:}$ The error sequence $ \langle e_\nu \rangle$ allows statements about the error statistics, for example whether the errors are so-called
- statistically independent errors, or
- bundle errors.
The following example is intended to illustrate these two types of errors.
$\text{Example 2:}$ In the following graph, we see the BMP image "White" with $300 × 200$ pixels in the center. The left image shows the falsification with statistically independent errors ⇒ "BSC model", while the right image illustrates a bundle error channel ⇒ "Gilbert-Elliott model".
- It should be noted that "BMP graphics" are always saved line by line, which can be seen in the error bundles in the right image.
- The average error probability in both cases is $2.5\%$, which means that on average every $40$th pixel is falsified (here: white ⇒ black).
Example application of digital channel models
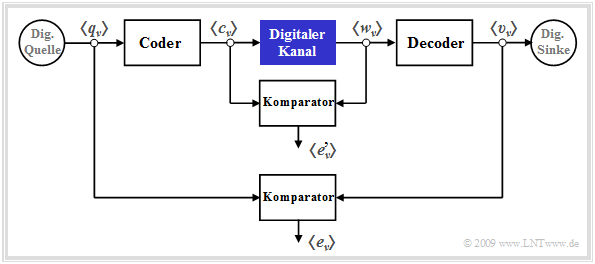
Digital channel models are preferably used for cascaded transmission, as shown in the following diagram.
You can see from this diagram:
- The inner transmission system – consisting of modulator, analog channel, noise, demodulator, receiver filter, decision and clock recovery – is summarized in the block "Digital channel" marked in blue.
- This inner block is characterized exclusively by its error sequence $ \langle e\hspace{0.05cm}'_\nu \rangle$, which refers to its input symbol sequence $ \langle c_\nu \rangle$ and output symbol sequence $ \langle w_\nu \rangle$. It is obvious that this channel model provides less information than a detailed analog model considering all components.
- In contrast, the "outer" error sequence $ \langle e_\nu \rangle$ refers to the source symbol sequence $ \langle q_\nu \rangle$ and the sink symbol sequence $ \langle v_\nu \rangle$ and thus to the overall system including the specific encoding and the decoder on the receiver side.
- The comparison of the two error sequences with and without consideration of encoder/decoder allows conclusions to be drawn about the efficiency of the underlying encoding and decoding. These two components are meaningful if and only if the outer comparator indicates fewer errors on average than the inner comparator.
Error sequence and average error probability
$\text{Definition:}$ The transmission behavior of a binary system is completely described by the error sequence $ \langle e_\nu \rangle$:
- \[e_{\nu} = \left\{ \begin{array}{c} 1 \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm if}\hspace{0.15cm}\upsilon_\nu \ne q_\nu \hspace{0.05cm}, \\ {\rm falls}\hspace{0.15cm} \upsilon_\nu = q_\nu \hspace{0.05cm}.\\ \end{array}\]
From this, the (average) bit error probability can be calculated as follows:
- \[p_{\rm M} = {\rm E}\big[e \big] = \lim_{N \rightarrow \infty} \frac{1}{N} \sum_{\nu = 1}^{N}e_{\nu}\hspace{0.05cm}.\]
It is assumed here that the random process generating the wrong decisions is "stationary" and "ergodic", so that the error sequence $ \langle e_\nu \rangle$ can also be formally described completely by the random variable $e \in \{0, \ 1\}$. Thus, the transition from time to coulter averaging is allowed.
Note: In all other $\rm LNTwww $ books, the mean bit error probability is denoted by $p_{\rm B}$. To avoid confusion in connection with the "Gilbert–Elliott model", this renaming here is unavoidable, and we will no longer refer to the bit error probability in the following, but only to the mean error probability $p_{\rm M}$.
Error correlation function
$\text{Definition:}$ An important descriptive quantity of the digital channel models is also the die error correlation function – abbreviated ECF:
- \[\varphi_{e}(k) = {\rm E}\big [e_{\nu} \cdot e_{\nu + k}\big ] = \overline{e_{\nu} \cdot e_{\nu + k} }\hspace{0.05cm}.\]
This has the following properties:
- $\varphi_{e}(k) $ indicates the (discrete-time) "auto-correlation function of the random variable $e$, which is also discrete-time. The sweeping line in the right equation denotes the time averaging.
- The error correlation value $\varphi_{e}(k) $ provides statistical information about two sequence elements that are $k$ apart, for example about $e_{\nu}$ and $e_{\nu+ k}$. The intervening elements $e_{\nu+ 1}$, ... , $e_{\nu+ k-1}$ do not affect the $\varphi_{e}(k)$ value.
- For stationary sequences, regardless of the error statistic due to $e \in \{0, \ 1\}$, always holds:
- \[\varphi_{e}(k = 0) = {\rm E}\big[e_{\nu} \cdot e_{\nu}\big] = {\rm E}\big[e^2\big]= {\rm E}\big[e\big]= {\rm Pr}(e = 1)= p_{\rm M}\hspace{0.05cm},\]
- \[\varphi_{e}(k \rightarrow \infty) = {\rm E}\big[e_{\nu}\big] \cdot {\rm E}\big[e_{\nu + k}\big] = p_{\rm M}^2\hspace{0.05cm}.\]
- The error correlation function is an at least weakly decreasing function. The slower the decay of the ECF values, the longer the memory of the channel and the further the statistical ties of the error sequence.
$\text{Example 3:}$ In a binary transmission, $100$ of the total $N = 10^5$ transmitted binary symbols are falsified, so that the error sequence $ \langle e_\nu \rangle$ consists of $100$ ones and $99900$ zeros.
- Thus, the average error probability is $p_{\rm M} =10^{-3}$.
- The error correlation function $\varphi_{e}(k)$ starts at $p_{\rm M} =10^{-3}$ $($for $k = 0)$ and tends towards $p_{\rm M}^2 =10^{-6}$ $($für $k = \to \infty)$ for very large $k$ values.
- So far, no statement can be made about the actual course of $\varphi_{e}(k)$ with the information given here.
Relationship between error sequence and error distance
$\text{Definition:}$ The error distance $a$ is the number of correctly transmitted symbols between two channel errors plus $1$.
The graphic illustrates this definition.
- Any information about the transmission behavior of the digital channel contained in the error sequence $ \langle e_\nu \rangle$ is also contained in the sequence $ \langle a_n \rangle$ of error distances.
- Since the sequences $ \langle e_\nu \rangle$ and $ \langle a_n \rangle$ are not synchronous, we use different indices $(\nu$ and $n)$.
In particular, we can see from the graph:
- Since the first symbol was transmitted correctly $(e_1 = 0)$ and the second incorrectly $(e_2 = 1)$, the error distance is $a_1 = 2$.
- $a_2 = 4$ indicates that three symbols were transmitted correctly between the first two errors $(e_2 = 1, \ e_5 = 1)$.
- If two errors follow each other directly, the error distance is equal to $1$, like $a_3$ in the graphic above.
- The event "$a = k$" means simultaneously $k-1$ error-free symbols between two errors.
- If an error occurred at time $\nu$, the next error follows at "$a = k$" exactly at time $\nu + k$.
- The set of values of the random variable $a$ is the set of natural numbers in contrast to the binary random variable $e$:
- \[a \in \{ 1, 2, 3, ... \}\hspace{0.05cm}, \hspace{0.5cm}e \in \{ 0, 1 \}\hspace{0.05cm}.\]
- The average error probability can be determined from both random variables:
- \[{\rm E}\big[e \big] = {\rm Pr}(e = 1) =p_{\rm M}\hspace{0.05cm}, \hspace{0.5cm} {\rm E}\big[a \big] = \sum_{k = 1}^{\infty} k \cdot {\rm Pr}(a = k) = {1}/{p_{\rm M}}\hspace{0.05cm}.\]
$\text{Example 4:}$ In the sketched sequence $16$ of the total $N = 40$ symbols are falsified ⇒ $p_{\rm M} = 0.4$. Accordingly, the expected value of the error distances gives
- \[{\rm E}\big[a \big] = 1 \cdot {4}/{16}+ 2 \cdot {5}/{16}+ 3 \cdot {4}/{16}+4 \cdot {1}/{16}+5 \cdot {2}/{16}= 2.5 = {1}/{p_{\rm M} }\hspace{0.05cm}.\]
Error distance distribution
The "probability density function" (PDF) of the discrete random variable $a \in \{1, 2, 3, \text{...}\}$ is composed of an (infinite) sum of Dirac delta functions according to the chapter "PDF definition for discrete random variables" in the book "Stochastic Signal Theory":
- \[f_a(a) = \sum_{k = 1}^{\infty} {\rm Pr}(a = k) \cdot \delta (a-k)\hspace{0.05cm}.\]
We refer to this particular PDF as the error distance density function. Based on the error sequence, the probability that the error distance $a$ is exactly equal to $k$ can be expressed by the following conditional probability:
- \[{\rm Pr}(a = k) = {\rm Pr}(e_{\nu + 1} = 0 \hspace{0.15cm}\cap \hspace{0.15cm} \text{...} \hspace{0.15cm}\cap \hspace{0.15cm}\hspace{0.05cm} e_{\nu + k -1} = 0 \hspace{0.15cm}\cap \hspace{0.15cm}e_{\nu + k} = 1 \hspace{0.1cm}| \hspace{0.1cm} e_{\nu } = 1)\hspace{0.05cm}.\]
In the book "Stochastic Signal Theory" you will also find the definition of the "distribution function" of the discrete random variable $a$:
- \[F_a(k) = {\rm Pr}(a \le k) \hspace{0.05cm}.\]
This function is obtained from the PDF $f_a(a)$ by integration from $1$ to $k$. The function $F_a(k)$ can take values between $0$ and $1$ (including these two limits) and is weakly monotonically increasing.
In the context of digital channel models, the literature deviates from this usual definition.
$\text{Definition:}$ Rather, here the error distance distribution (EDD) gives the probability that the error distance $a$ is greater than or equal to $k$:
- \[V_a(k) = {\rm Pr}(a \ge k) = 1 - \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa)\hspace{0.05cm}.\]
In particular:
- $$V_a(k = 1) = 1 \hspace{0.05cm},\hspace{0.5cm} \lim_{k \rightarrow \infty}V_a(k ) = 0 \hspace{0.05cm}.$$
The following relationship holds between the monotonically increasing function $F_a(k)$ and the monotonically decreasing function $V_a(k)$:
- \[F_a(k ) = 1-V_a(k +1) \hspace{0.05cm}.\]
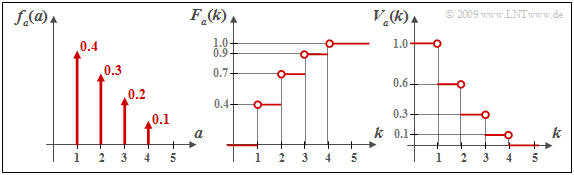
$\text{Example 5:}$ The graph shows in the left sketch an arbitrary discrete error distance density function $f_a(a)$ and the resulting cumulative functions
- $F_a(k ) = {\rm Pr}(a \le k)$ ⇒ middle sketch, as well as
- $V_a(k ) = {\rm Pr}(a \ge k)$ ⇒ right sketch.
For example, for $k = 2$, we obtain:
- \[F_a( k =2 ) = {\rm Pr}(a = 1) + {\rm Pr}(a = 2) \hspace{0.05cm}, \]
- \[\Rightarrow \hspace{0.3cm} F_a( k =2 ) = 1-V_a(k = 3)= 0.7\hspace{0.05cm}, \]
- \[ V_a(k =2 ) = 1 - {\rm Pr}(a = 1) \hspace{0.05cm},\]
- \[\Rightarrow \hspace{0.3cm} V_a(k =2 ) = 1-F_a(k = 1) = 0.6\hspace{0.05cm}.\]
For $k = 4$, the following results are obtained:
- \[F_a(k = 4 ) = {\rm Pr}(a \le 4) = 1 \hspace{0.05cm}, \hspace{0.5cm} V_a(k = 4 ) = {\rm Pr}(a \ge 4)= {\rm Pr}(a = 4) = 0.1 = 1-F_a(k = 3) \hspace{0.05cm}.\]
Exercises for the chapter
Exercise 5.1: Error Distance Distribution
Exercise 5.2: Error Correlation Function