Contents
- 1 # OVERVIEW OF THE FIFTH MAIN CHAPTER #
- 2 Application of analog channel models
- 3 Definition of digital channel models
- 4 Beispielhafte Anwendung von digitalen Kanalmodellen
- 5 Fehlerfolge und mittlere Fehlerwahrscheinlichkeit
- 6 Fehlerkorrelationsfunktion
- 7 Zusammenhang zwischen Fehlerfolge und Fehlerabstand
- 8 Fehlerabstandsverteilung
- 9 Aufgaben zum Kapitel
# OVERVIEW OF THE FIFTH MAIN CHAPTER #
At the end of the book "Digital Signal Transmission", digital channel models are discussed which do not describe the transmission behavior of a digital transmission system in great detail according to the individual system components, but rather globally on the basis of typical error structures. Such channel models are mainly used for cascaded transmission systems for the inner block, if the performance of the outer system components - for example, coder and decoder - is to be determined by simulation. The following are dealt with in detail:
- the descriptive variables error correlation function and error distance distribution,
- the BSC model (Binary Symmetric Channel ) for the description of statistically independent errors,
- the bundle error channel models according to Gilbert-Elliott and McCullough,
- the Wilhelm channel model for the formulaic approximation of measured error curves,
- some notes on the generation of fault sequences, for example with respect to error distance simulation,
- the effects of different error structures on BMP files ⇒ images and WAV files ⇒ audios.
Note: All BMP images and WAV audios of this chapter were generated with the Windows program "Digital Channel Models & Multimedia" from the (former) practical course "Simulation of Digital Transmission Systems " at the Chair of Communications Engineering of the TU Munich.
Application of analog channel models
For investigations of message transmission systems, suitable channel models are of great importance, because they are the
- prerequisite for system simulation and optimization, as well as
- creating consistent and reconstructible boundary conditions.
For digital signal transmission, there are both analog and digital channel models:
- Although an analog channel model does not have to reproduce the transmission channel in all physical details, it should describe its transmission behavior, including the dominant noise variables, with sufficient functional accuracy.
- In most cases, a compromise must be found between mathematical manageability and the relationship to reality.
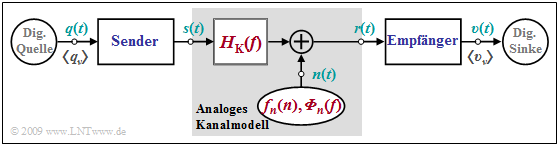
$\text{Example 1:}$ The graphic shows an analog channel model within a digital transmission system. This contains
- the "channel frequency response" $H_{\rm K}(f)$ to describe the linear distortions, and
- an additive noise signal $n(t)$, characterized by the "probability density function" (PDF) $f_n(n)$ and the "power-spectral density" (PSD) ${\it \Phi}_n(f)$.
A special case of this model is the so-called "AWGN channel" (Additive White Gaussian Noise) with the system properties
- \[H_{\rm K}(f) = 1\hspace{0.05cm},\hspace{0.2cm}{\it \Phi}_{n}(f) = {\rm const.}\hspace{0.05cm},\hspace{0.2cm} {f}_{n}(n) = \frac{1}{\sqrt{2 \pi} \cdot \sigma} \cdot {\rm e}^{-n^2\hspace{-0.05cm}/(2 \sigma^2)}\hspace{0.05cm}.\]
This simple model is suitable, for example, for describing a radio channel with time-invariant behavior, where the model is abstracted such that
- the actual band-pass channel is described in the equivalent low-pass range, and
- the attenuation, which depends on the frequency band and the transmission path length, is offset against the variance $\sigma^2$ of the noise signal $n(t)$.
To take time-variant characteristics into account, one must use other models such as "Rayleigh ading", "Rice fading" and "Lognormal fading",
which are described in the book "Mobile communications".
For wired transmission systems, the specific frequency response of the transmission medium according to the specifications for "coaxial cable" and "two-wire line" in the book "Linear Time-Invariant Systems" must be taken into account in particular, but also the fact that white noise can no longer be assumed due to "extraneous noise" (crosstalk, electromagnetic fields, etc.).
In the case of optical systems, the multiplicatively acting, i.e. signal-dependent "shot noise" must also be suitably incorporated into the analog channel model.
Definition of digital channel models
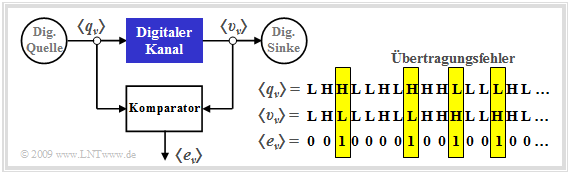
An analog channel model is characterized by analog input and output variables. In contrast, in a digital channel model (sometimes referred to as "discrete"), both the input and the output are discrete in time and value. In the following, let these be the source symbol sequence $ \langle q_\nu \rangle$ with $ q_\nu \in \{\rm L, \ H\}$ and the sink symbol sequence $ \langle v_\nu \rangle$ with $ v_\nu \in \{\rm L, \ H\}$. The indexing variable $\nu$ can take values between $1$ and $N$.
Wie ein Vergleich mit dem Blockschaltbild im $\text{Beispiel 1}$ zeigt, ist der "Digitale Kanal" ein vereinfachendes Modell des analogen Übertragungskanals einschließlich der technischen Sende– und Empfangseinrichtungen. Vereinfachend deshalb, weil dieses Modell sich lediglich auf die auftretenden Übertragungsfehler bezieht, dargestellt durch die Fehlerfolge $ \langle e_\nu \rangle$ mit
- \[e_{\nu} = \left\{ \begin{array}{c} 1 \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm falls}\hspace{0.15cm}\upsilon_\nu \ne q_\nu \hspace{0.05cm}, \\ {\rm falls}\hspace{0.15cm} \upsilon_\nu = q_\nu \hspace{0.05cm}.\\ \end{array}\]
Während $\rm L$ und $\rm H$ die möglichen Symbole bezeichnen, die hier für Low und High stehen, ist $ e_\nu \in \{\rm 0, \ 1\}$ ein reeller Zahlenwert. Oft werden die Symbole auch als $ q_\nu \in \{\rm 0, \ 1\}$ und $ v_\nu \in \{\rm 0, \ 1\}$ definiert. Um Verwechslungen zu vermeiden, haben wir hier die etwas ungewöhnliche Nomenklatur verwendet.
Die in der Grafik angegebene Fehlerfolge $ \langle e_\nu \rangle$
- ergibt sich durch den Vergleich der beiden Binärfolgen $ \langle q_\nu \rangle$ und $ \langle v_\nu \rangle$,
- beinhaltet nur Informationen über die Abfolge der Übertragungsfehler und damit weniger Information als ein analoges Kanalmodell,
- wird zweckmäßigerweise durch einen Zufallsprozess mit nur wenigen Parametern angenähert.
$\text{Fazit:}$ Die Fehlerfolge $ \langle e_\nu \rangle$ erlaubt Aussagen über die Fehlerstatistik, zum Beispiel ob es sich um so genannte
- statistisch unabhängige Fehler, oder
- Bündelfehler
handelt. Das folgende Beispiel soll diese beiden Fehlerarten verdeutlichen.
$\text{Beispiel 2:}$ In der folgenden Grafik sehen wir in der Mitte das BMP–Bild "Weiß" mit $300 × 200$ Pixeln. Das linke Bild zeigt die Verfälschung mit statistisch unabhängigen Fehlern ⇒ BSC–Modell, während das rechte Bild einen Bündelfehlerkanal ⇒ Gilbert–Elliott–Modell verdeutlicht.
- Anzumerken ist, dass BMP–Grafiken stets zeilenweise abgespeichert werden, was an den Fehlerbündeln im rechten Bild zu erkennen ist.
- Die mittlere Fehlerwahrscheinlichkeit beträgt in beiden Fällen $2.5\%$, das heißt, dass im Mittel jedes $40.$ Pixel verfälscht ist (hier: weiß ⇒ schwarz).
Beispielhafte Anwendung von digitalen Kanalmodellen
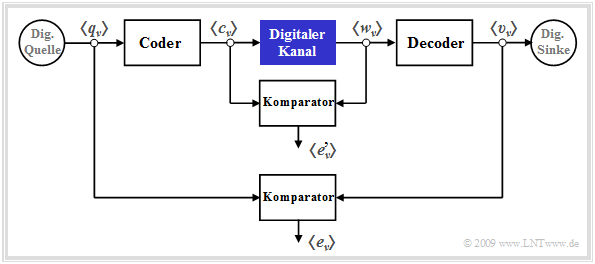
Digitale Kanalmodelle finden vorzugsweise Anwendung bei einer kaskadierten Übertragung, wie in der folgenden Grafik dargestellt.
Man erkennt aus dieser Darstellung:
- Das innere Übertragungssystem – bestehend aus Modulator, Analogkanal, Störung, Demodulator, Empfangsfilter, Entscheider und Taktrückgewinnung – ist im blau markierten Block "Digitaler Kanal" zusammengefasst.
- Dieser innere Block wird auschließlich durch seine Fehlerfolge $ \langle e\hspace{0.05cm}'_\nu \rangle$ charakterisiert, die sich auf seine Eingangssymbolfolge $ \langle c_\nu \rangle$ und Ausgangssymbolfolge $ \langle w_\nu \rangle$ bezieht. Es ist offensichtlich, dass dieses Kanalmodell weniger Informationen liefert als ein detailliertes Analogmodell unter Berücksichtigung aller Komponenten.
- Dagegen bezieht sich die "äußere" Fehlerfolge $ \langle e_\nu \rangle$ auf die Quellensymbolfolge $ \langle q_\nu \rangle$ und die Sinkensymbolfolge $ \langle v_\nu \rangle$ und damit auf das Gesamtsystem einschließlich der spezifischen Codierung und des empfängerseitigen Decoders.
- Der Vergleich der beiden Fehlerfolgen mit und ohne Berücksichtigung von Coder/Decoder erlaubt Rückschlüsse auf die Effizienz der zugrundeliegenden Codierung und Decodierung. Diese beiden Komponenten sind dann und nur dann sinnvoll, wenn der äußere Komparator im Mittel weniger Fehler anzeigt als der innere.
Fehlerfolge und mittlere Fehlerwahrscheinlichkeit
$\text{Definition:}$ Das Übertragungsverhalten eines Binärsystems wird durch die Fehlerfolge $ \langle e_\nu \rangle$ vollständig beschrieben:
- \[e_{\nu} = \left\{ \begin{array}{c} 1 \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm falls}\hspace{0.15cm}\upsilon_\nu \ne q_\nu \hspace{0.05cm}, \\ {\rm falls}\hspace{0.15cm} \upsilon_\nu = q_\nu \hspace{0.05cm}.\\ \end{array}\]
Hieraus lässt sich die (mittlere) Bitfehlerwahrscheinlichkeit wie folgt berechnen:
- \[p_{\rm M} = {\rm E}\big[e \big] = \lim_{N \rightarrow \infty} \frac{1}{N} \sum_{\nu = 1}^{N}e_{\nu}\hspace{0.05cm}.\]
Vorausgesetzt ist hierbei, dass der die Fehlentscheidungen erzeugende Zufallsprozess stationär und ergodisch ist, so dass man die Fehlerfolge $ \langle e_\nu \rangle$ formal auch durch die Zufallsgröße $e \in \{0, \ 1\}$ vollständig beschreiben kann. Der Übergang von der Zeit– zur Scharmittelung ist also zulässig.
Hinweis: In allen anderen $\rm LNTwww $–Büchern wird die mittlere Bitfehlerwahrscheinlichkeit mit $p_{\rm B}$ bezeichnet. Zur Vermeidung von Verwechslungen im Zusammenhang mit dem Gilbert–Elliott–Modell ist diese hier vorgenommene Umbenennung unvermeidbar und wir sprechen nachfolgend nicht mehr von der Bitfehlerwahrscheinlichkeit, sondern nur noch von der mittleren Fehlerwahrscheinlichkeit $p_{\rm M}$.
Fehlerkorrelationsfunktion
$\text{Definition:}$ Eine wichtige Beschreibungsgröße der digitalen Kanalmodelle ist auch die Fehlerkorrelationsfunktion – abgekürzt FKF:
- \[\varphi_{e}(k) = {\rm E}\big [e_{\nu} \cdot e_{\nu + k}\big ] = \overline{e_{\nu} \cdot e_{\nu + k} }\hspace{0.05cm}.\]
Diese weist folgende Eigenschaften auf:
- $\varphi_{e}(k) $ gibt die (zeitdiskrete) Autokorrelationsfunktion der ebenfalls zeitdiskreten Zufallsgröße $e$ an. Die überstreichende Linie in der rechten Gleichung kennzeichnet die Zeitmittelung.
- Der Fehlerkorrelationswert $\varphi_{e}(k) $ liefert statistische Aussagen bezüglich zwei um $k$ auseinander liegende Folgenelemente, zum Beispiel über $e_{\nu}$ und $e_{\nu+ k}$. Die dazwischen liegenden Elemente $e_{\nu+ 1}$, ... , $e_{\nu+ k-1}$ beeinflussen den $\varphi_{e}(k)$–Wert nicht.
- Bei stationren Folgen gilt unabhängig von der der Fehlerstatistik wegen $e \in \{0, \ 1\}$ stets:
- \[\varphi_{e}(k = 0) = {\rm E}\big[e_{\nu} \cdot e_{\nu}\big] = {\rm E}\big[e^2\big]= {\rm E}\big[e\big]= {\rm Pr}(e = 1)= p_{\rm M}\hspace{0.05cm},\]
- \[\varphi_{e}(k \rightarrow \infty) = {\rm E}\big[e_{\nu}\big] \cdot {\rm E}\big[e_{\nu + k}\big] = p_{\rm M}^2\hspace{0.05cm}.\]
- Die Fehlerkorrelationsfunktion ist eine zumindest schwach abfallende Funktion. Je langsamer der Abfall der FKF–Werte erfolgt, desto länger ist das Gedächtnis des Kanals und um so weiter reichen die statistischen Bindungen der Fehlerfolge.
$\text{Beispiel 3:}$ Bei einer Binärübertragung werden $100$ der insgesamt $N = 10^5$ übertragenen Binärsymbole verfälscht, so dass die Fehlerfolge $ \langle e_\nu \rangle$ aus $100$ Einsen und $99900$ Nullen besteht.
- Die mittlere Fehlerwahrscheinlichkeit beträgt somit $p_{\rm M} =10^{-3}$.
- Die Fehlerkorrelationsfunktion $\varphi_{e}(k)$ beginnt bei $p_{\rm M} =10^{-3}$ $($für $k = 0)$ und tendiert für sehr große $k$–Werte gegen $p_{\rm M}^2 =10^{-6}$ $($für $k = \to \infty)$.
- Über den tatsächlichen Verlauf von $\varphi_{e}(k)$ ist mit den hier gemachten Angaben bisher noch keine Aussage möglich.
Zusammenhang zwischen Fehlerfolge und Fehlerabstand
$\text{Definition:}$ Als Fehlerabstand $a$ bezeichnet man die Anzahl der zwischen zwei Kanalfehlern richtig übertragenen Symbole plus $1$.
Die Grafik verdeutlicht diese Definition.
- Jede in der Fehlerfolge $ \langle e_\nu \rangle$ enthaltene Information über das Übertragungsverhalten des digitalen Kanals ist auch in der Folge $ \langle a_n \rangle$ der Fehlerabstände enthalten.
- Da die Folgen $ \langle e_\nu \rangle$ und $ \langle a_n \rangle$ nicht synchron laufen, verwenden wir unterschiedliche Indizes $(\nu$ bzw. $n)$.
Aus der Grafik erkennt man insbesondere:
- Da das erste Symbol richtig übertragen wurde $(e_1 = 0)$ und das zweite falsch $(e_2 = 1)$, ist der Fehlerabstand $a_1 = 2$.
- $a_2 = 4$ sagt aus, dass zwischen den beiden ersten Fehlern $(e_2 = 1, \ e_5 = 1)$ drei Symbole richtig übertragen wurden.
- Folgen zwei Fehler direkt aufeinander, so ist der Fehlerabstand wie $a_3$ in obiger Grafik gleich $1$.
- Das Ereignis "$a = k$" bedeutet gleichzeitig $k-1$ fehlerfreie Symbole zwischen zwei Fehlern.
- Ist zum Zeitpunkt $\nu$ ein Fehler aufgetreten, so folgt bei "$a = k$" der nächste Fehler genau zum Zeitpunkt $\nu + k$.
- Der Wertevorrat der Zufallsgröße $a$ ist die Menge der natürlichen Zahlen im Gegensatz zur binären Zufallsgröße $e$:
- \[a \in \{ 1, 2, 3, ... \}\hspace{0.05cm}, \hspace{0.5cm}e \in \{ 0, 1 \}\hspace{0.05cm}.\]
- Die mittlere Fehlerwahrscheinlichkeit lässt sich aus beiden Zufallsgrößen ermitteln:
- \[{\rm E}\big[e \big] = {\rm Pr}(e = 1) =p_{\rm M}\hspace{0.05cm}, \hspace{0.5cm} {\rm E}\big[a \big] = \sum_{k = 1}^{\infty} k \cdot {\rm Pr}(a = k) = {1}/{p_{\rm M}}\hspace{0.05cm}.\]
$\text{Beispiel 4:}$ In der skizzierten Folge sind $16$ der insgesamt $N = 40$ Symbole verfälscht ⇒ $p_{\rm M} = 0.4$. Der Erwartungswert der Fehlerabstände ergibt entsprechend
- \[{\rm E}\big[a \big] = 1 \cdot {4}/{16}+ 2 \cdot {5}/{16}+ 3 \cdot {4}/{16}+4 \cdot {1}/{16}+5 \cdot {2}/{16}= 2.5 = {1}/{p_{\rm M} }\hspace{0.05cm}.\]
Fehlerabstandsverteilung
Die Wahrscheinlichkeitsdichtefunktion (WDF) der diskreten Zufallsgröße $a \in \{1, 2, 3, \text{...}\}$ setzt sich entsprechend dem Kapitel WDF-Definition für diskrete Zufallsgrößen im Buch "Stochastische Signaltheorie" aus einer (unendlichen) Summe von Diracfunktionen zusammen:
- \[f_a(a) = \sum_{k = 1}^{\infty} {\rm Pr}(a = k) \cdot \delta (a-k)\hspace{0.05cm}.\]
Wir bezeichnen diese spezielle WDF als Fehlerabstandsdichtefunktion. Die Wahrscheinlichkeit, dass der Fehlerabstand $a$ exakt gleich $k$ ist, lässt sich anhand der Fehlerfolge durch die folgende bedingte Wahrscheinlichkeit ausdrücken:
- \[{\rm Pr}(a = k) = {\rm Pr}(e_{\nu + 1} = 0 \hspace{0.15cm}\cap \hspace{0.15cm} \text{...} \hspace{0.15cm}\cap \hspace{0.15cm}\hspace{0.05cm} e_{\nu + k -1} = 0 \hspace{0.15cm}\cap \hspace{0.15cm}e_{\nu + k} = 1 \hspace{0.1cm}| \hspace{0.1cm} e_{\nu } = 1)\hspace{0.05cm}.\]
Im Buch "Stochastische Signaltheorie" finden Sie ebenfalls die Definition der Verteilungsfunktion der diskreten Zufallsgröße $a$:
- \[F_a(k) = {\rm Pr}(a \le k) \hspace{0.05cm}.\]
Diese Funktion ergibt sich aus der WDF $f_a(a)$ durch Integration von $1$ bis $k$. Die Funktion $F_a(k)$ kann Werte zwischen $0$ und $1$ (einschließlich dieser beiden Grenzen) annehmen und ist schwach monoton ansteigend.
Im Zusammenhang mit den digitalen Kanalmodellen wird in der Literatur von dieser üblichen Definition abgewichen.
$\text{Definition:}$ Vielmehr gibt hier die Fehlerabstandsverteilung (FAV) die Wahrscheinlichkeit an, dass der Fehlerabstand $a$ größer oder gleich $k$ ist:
- \[V_a(k) = {\rm Pr}(a \ge k) = 1 - \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa)\hspace{0.05cm}.\]
Insbesondere gilt:
- $$V_a(k = 1) = 1 \hspace{0.05cm},\hspace{0.5cm} \lim_{k \rightarrow \infty}V_a(k ) = 0 \hspace{0.05cm}.$$
Zwischen der monoton ansteigenden Funktion $F_a(k)$ und der monoton abfallenden Funktion $V_a(k)$ gilt folgender Zusammenhang:
- \[F_a(k ) = 1-V_a(k +1) \hspace{0.05cm}.\]
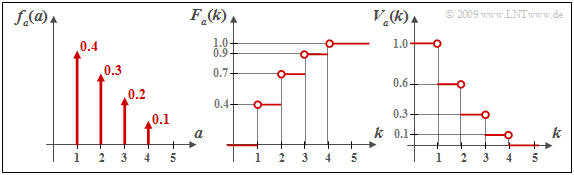
$\text{Beispiel 5:}$ Die Grafik zeigt in der linken Skizze eine willkürliche diskrete Fehlerabstandsdichtefunktion $f_a(a)$ und die daraus resultierenden kumulativen Funktionen
- $F_a(k ) = {\rm Pr}(a \le k)$ ⇒ mittlere Skizze, sowie
- $V_a(k ) = {\rm Pr}(a \ge k)$ ⇒ rechte Skizze.
Beispielsweise ergibt sich für $k = 2$:
- \[F_a( k =2 ) = {\rm Pr}(a = 1) + {\rm Pr}(a = 2) \hspace{0.05cm}, \]
- \[\Rightarrow \hspace{0.3cm} F_a( k =2 ) = 1-V_a(k = 3)= 0.7\hspace{0.05cm}, \]
- \[ V_a(k =2 ) = 1 - {\rm Pr}(a = 1) \hspace{0.05cm},\]
- \[\Rightarrow \hspace{0.3cm} V_a(k =2 ) = 1-F_a(k = 1) = 0.6\hspace{0.05cm}.\]
Für $k = 4$ erhält man folgende Resultate:
- \[F_a(k = 4 ) = {\rm Pr}(a \le 4) = 1 \hspace{0.05cm}, \hspace{0.5cm} V_a(k = 4 ) = {\rm Pr}(a \ge 4)= {\rm Pr}(a = 4) = 0.1 = 1-F_a(k = 3) \hspace{0.05cm}.\]
Aufgaben zum Kapitel
Aufgabe 5.1: Fehlerabstandsverteilung
Aufgabe 5.2: Fehlerkorrelationsfunktion