Difference between revisions of "Digital Signal Transmission/Properties of Nyquist Systems"
| Line 173: | Line 173: | ||
*In the limiting case $r \to 0$, both cases yield the rectangular Nyquist spectrum and the $\rm si$–shaped Nyquist pulse, which decays asymptotically with $1/t$ (thin green curves). | *In the limiting case $r \to 0$, both cases yield the rectangular Nyquist spectrum and the $\rm si$–shaped Nyquist pulse, which decays asymptotically with $1/t$ (thin green curves). | ||
*For an average rolloff $(r \approx 0.5)$, the first overshoots are smaller for the trapezoidal spectrum than for the CRO spectrum, because here the Nyquist slope is flatter for a given $r$ (blue curves). | *For an average rolloff $(r \approx 0.5)$, the first overshoots are smaller for the trapezoidal spectrum than for the CRO spectrum, because here the Nyquist slope is flatter for a given $r$ (blue curves). | ||
| − | *With the rolloff factor $r = 1$, the trapezoid becomes a triangle in the frequency domain and the CRO spectrum becomes the ''cosine–square spectrum''. In the diagrams on the [[Digital_Signal_Transmission/ | + | *With the rolloff factor $r = 1$, the trapezoid becomes a triangle in the frequency domain and the CRO spectrum becomes the ''cosine–square spectrum''. In the diagrams on the [[Digital_Signal_Transmission/Properties_of_Nyquist_Systems#1.2FT_Nyquist_spectra|last page]] these spectral functions are drawn in red. |
| − | * | + | *With $r = 1$ the asymptotic decay of the upper time function (according to the trapezoidal spectrum) occurs with $1/t^2$ and the decay of the lower time function (according to the CRO spectrum) with $1/t^3$. |
| − | * | + | *This means: After a longer time, the CRO Nyquist pulse has settled better than the trapezoidal Nyquist pulse. |
| − | == | + | == Second Nyquist criterion== |
<br> | <br> | ||
| − | + | Before the exact mathematical definition, the significance of the ''second Nyquist criterion'' for the evaluation of a digital system is illustrated by means of diagrams. The diagram shows three examples of Nyquist systems: | |
| − | * | + | *at the top, the Nyquist spectrum $G_d(f)$, |
| − | * | + | *below the corresponding eye diagram referring to the [[Digital_Signal_Transmission/Fehlerwahrscheinlichkeit_unter_Berücksichtigung_von_Impulsinterferenzen#Definition_und_Aussagen_des_Augendiagramms|third main chapter]]. |
| − | [[File:EN_Dig_T_1_3_S4.png|right|frame| | + | [[File:EN_Dig_T_1_3_S4.png|right|frame|Clarification of first and second Nyquist criterion]] |
''Interpretation:'' | ''Interpretation:'' | ||
| − | * | + | *The diagram on the left shows the eye diagram of a Nyquist system with cosine rolloff characteristic, where the rolloff factor $r= 0.5$ was chosen. Since the first Nyquist criterion is fulfilled here (there is point symmetry around the Nyquist frequency $f_{\rm Nyq}$, the largest possible value for the vertical eye opening at time $t = 0$ is $2 \cdot g_d(0)$. All eye lines pass through one of the two points marked in red at time $t = 0$ ⇒ the eye is vertically maximally open. |
| − | * | + | *The middle spectrum does not show any symmetry with respect to the rolloff, so that the first Nyquist criterion is not fulfilled here – in contrast to the second one. All eyelines here intersect the time axis at the same times (marked by the green dots), which facilitates, for example, clock recovery by means of a PLL (<i>Phase-Locked Loop</i> ). When the second Nyquist criterion is met, the horizontal eye opening is maximally equal to the symbol duration $T$ ⇒ the eye is maximally open horizontally. |
| − | * | + | *The right eye diagram illustrates that for the CRO spectrum with $r = 1$, both the first and second Nyquist criteria are satisfied. The Nyquist pulse |
:$$g_d ( t )= g_0 \cdot \frac{\pi }{4}\cdot {\rm si} \left ( | :$$g_d ( t )= g_0 \cdot \frac{\pi }{4}\cdot {\rm si} \left ( | ||
\frac{\pi \cdot t}{T}\right)\cdot \left [ {\rm si}(\pi \cdot | \frac{\pi \cdot t}{T}\right)\cdot \left [ {\rm si}(\pi \cdot | ||
(\frac{t}{T} + \frac{1}{2}) + {\rm si}(\pi \cdot (\frac{t}{T} - | (\frac{t}{T} + \frac{1}{2}) + {\rm si}(\pi \cdot (\frac{t}{T} - | ||
\frac{1}{2})\right]$$ | \frac{1}{2})\right]$$ | ||
| − | : | + | :here exhibits the required zero crossings at $t = \pm T$, $t = \pm 1.5T$, $t = \pm 2T$, $t = \pm 2.5T$, ... but not at $t = \pm 0.5T$. The pulse amplitude is $g_d(t = 0) = g_0$. ''Note:'' No other pulse satisfies both the first and second Nyquist criteria simultaneously. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Summary of Nyquist criteria:}$<br><br> |
| − | '''(1)''' In | + | '''(1)''' In memory of the physicist [https://en.wikipedia.org/wiki/Harry_Nyquist Harry Nyquist] we denote a basic detection pulse $g_d( t)$ with the properties |
| − | :$$g_d ( t= 0) \ne 0, \hspace{1cm} g_d ( t)= 0 \hspace{0.3cm}{\rm{ | + | :$$g_d ( t= 0) \ne 0, \hspace{1cm} g_d ( t)= 0 \hspace{0.3cm}{\rm{for} }\hspace{0.3cm} |
t = \pm T, \pm 2T,\pm 3T,\hspace{0.05cm}\text{...}$$ | t = \pm T, \pm 2T,\pm 3T,\hspace{0.05cm}\text{...}$$ | ||
| − | : | + | :as the Nyquist–1 pulse $g_{\hspace{0.05cm}\rm Nyq-1}(t)$. This satisfies the first Nyquist criterion and leads to the maximum vertical eye opening. |
| − | '''(2)''' | + | '''(2)''' A pulse $g_{\hspace{0.05cm}\rm Nyq-2}(t)$ satisfying the second Nyquist criterion must have zero crossings at $t = \pm 1.5T$, $t = \pm 2.5T$, ... have: |
| − | :$$g_d ( t= 0.5) \ne 0, \hspace{0.8cm} g_d ( t)= 0 \hspace{0.3cm}{\rm{ | + | :$$g_d ( t= 0.5) \ne 0, \hspace{0.8cm} g_d ( t)= 0 \hspace{0.3cm}{\rm{for} }\hspace{0.3cm} |
t = \pm 1.5T, \ \pm 2.5T,\ \pm 3.5T,\hspace{0.05cm}\text{...}$$ | t = \pm 1.5T, \ \pm 2.5T,\ \pm 3.5T,\hspace{0.05cm}\text{...}$$ | ||
| − | : | + | :Such a Nyquist–2 pulse leads to the maximum horizontal eye opening. |
| − | '''(3)''' | + | '''(3)''' A Nyquist–2 pulse can always be represented as the sum of two Nyquist–1 pulses shifted by $t = \pm T/2$: |
:$$g_{\rm Nyq-2} ( t )= g_{\rm Nyq-1} ( t +T/2)+g_{\rm Nyq-1} ( t -T/2)\hspace{0.05cm}.$$ | :$$g_{\rm Nyq-2} ( t )= g_{\rm Nyq-1} ( t +T/2)+g_{\rm Nyq-1} ( t -T/2)\hspace{0.05cm}.$$ | ||
| − | '''(4)''' | + | '''(4)''' In the frequency domain, the second Nyquist criterion (see [ST85] <ref>Söder, G.; Tröndle, K.: ''Digitale Übertragungssysteme - Theorie, Optimierung & Dimensionierung der Basisbandsysteme.'' Berlin – Heidelberg: Springer, 1985.</ref>) is: |
:$$\sum_{k = -\infty}^{+\infty} \frac {G_d \left ( f -k/T | :$$\sum_{k = -\infty}^{+\infty} \frac {G_d \left ( f -k/T | ||
\right)}{\cos(\pi \cdot f \cdot T - k \cdot \pi)}= {\rm const.}$$}} | \right)}{\cos(\pi \cdot f \cdot T - k \cdot \pi)}= {\rm const.}$$}} | ||
| Line 220: | Line 220: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 3:}$ Starting from the Nyquist–1 pulse $g_{\rm Nyq-1}( t )= g_0 \cdot {\rm si}(\pi \cdot t/T)$ the corresponding Nyquist–2 pulse is: |
:$$g_{\rm Nyq-2}( t ) = g_0 \cdot \left [ {\rm si}(\pi \cdot \frac{t + T/2}{T}) + {\rm si}(\pi \cdot \frac{t- T/2}{T}) \right] =\frac{2 \cdot g_0}{\pi} \cdot \frac{\cos(\pi \cdot t/T)}{1 - (2 \cdot t/T)^2}\hspace{0.05cm}.$$ | :$$g_{\rm Nyq-2}( t ) = g_0 \cdot \left [ {\rm si}(\pi \cdot \frac{t + T/2}{T}) + {\rm si}(\pi \cdot \frac{t- T/2}{T}) \right] =\frac{2 \cdot g_0}{\pi} \cdot \frac{\cos(\pi \cdot t/T)}{1 - (2 \cdot t/T)^2}\hspace{0.05cm}.$$ | ||
| − | * | + | *Due to the limitation of the spectrum $G_{\rm Nyq-1}( f)$ to the range $\vert f \vert \le f_{\rm Nyq} = 1/(2T)$, in equation '''(4)''' above the sum is limited to the term with $k = 0$ and we obtain: |
:$$G_{\rm Nyq-2}(f) = \left\{ \begin{array}{c} g_0 \cdot T \cdot \cos(\pi/2 \cdot f/f_{\rm Nyq}) \\ | :$$G_{\rm Nyq-2}(f) = \left\{ \begin{array}{c} g_0 \cdot T \cdot \cos(\pi/2 \cdot f/f_{\rm Nyq}) \\ | ||
\\ 0 \\\end{array} \right.\quad | \\ 0 \\\end{array} \right.\quad | ||
| − | \begin{array}{*{1}c} {\rm{ | + | \begin{array}{*{1}c} {\rm{for} }\hspace{0.15cm} \vert f \vert < f_{\rm |
Nyq}\hspace{0.05cm}, | Nyq}\hspace{0.05cm}, | ||
| − | \\ \\ {\rm{ | + | \\ \\ {\rm{otherwise} }\hspace{0.05cm}. \\ |
\end{array}$$ | \end{array}$$ | ||
| − | * | + | *This frequency response and the corresponding eye diagram is sketched in the middle column of the above diagram. |
| − | * | + | *From the bottom diagram, one can clearly see the fulfillment of the second Nyquist criterion.}} |
| − | == | + | == Exercises for the chapter == |
<br> | <br> | ||
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_1.4:_Nyquist_Criteria|Exercise 1.4: Nyquist Criteria]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_1.4Z:_Complex_Nyquist_Spectrum|Exercise 1.4Z: Complex Nyquist Spectrum]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_1.5:_Cosine-Square_Spectrum|Exercise 1.5: Cosine-Square Spectrum]] |
| − | == | + | ==References== |
<references/> | <references/> | ||
Revision as of 16:08, 7 March 2022
Contents
First Nyquist criterion in the time domain
For the entire first main chapter it was assumed that the detection of a symbol should not be affected by neighboring pulses. This is achieved by the detection of the signal
- $$d(t) = \sum \limits_{\it (\nu)} a_\nu \cdot g_d ( t - \nu T)$$
at the detection times $(\nu \cdot T)$ whenever the basic detection pulse $g_d(t)$
- is restricted to the range $|t| < T$, which was assumed for the last chapter Error Probability for Baseband Transmission, or
- has equidistant zero crossings at the detection times $\nu \cdot T$.
For the sake of simplicity, the noise component of the detection signal is assumed to be negligibly small in the following $(d_{\rm N}(t) =0)$.
$\text{Definition:}$ One denotes a basic detection pulse with the properties
- $$g_d ( t = \nu T)= 0 \hspace{0.3cm}{\rm{for} }\hspace{0.3cm} \nu = \pm 1, \pm 2,\pm 3,\hspace{0.05cm}\text{...}$$
as Nyquist pulse $g_{\hspace{0.05cm}\rm Nyq}(t)$, named after the physicist Harry Nyquist.
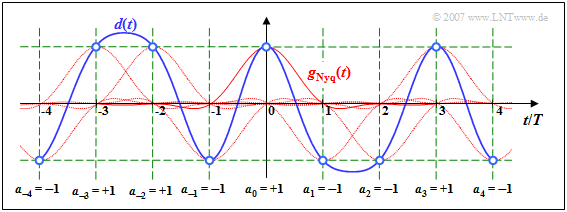
$\text{Example 1:}$ The diagram shows the detection signal $d(t)$ of such a Nyquist system. Dotted in red are the (weighted and shifted) Nyquist pulses $a_\nu \cdot g_{\hspace{0.05cm}\rm Nyq}(t -\nu \cdot T)$.
Please note:
- At the detection times, $d(\nu \cdot T) = a_\nu \cdot g_{\hspace{0.05cm}\rm Nyq}(0)$, as shown by the blue circles and green grid.
- The trailing pulses of the preceding pulses $(\nu < 0)$ as well as the leading pulses of the following pulses $(\nu > 0)$ do not affect the detection of the symbol $a_0$ in the Nyquist system.
For the sake of completeness, it should be mentioned that for this diagram the basic detection pulse
- $$g_{\hspace{0.05cm}\rm Nyq} ( t )= g_0 \cdot {\rm si} \left ( \frac{\pi \cdot t}{T}\right)\cdot {\rm si} \left ( \frac{\pi \cdot t}{2 \cdot T}\right)$$
with trapezoidal spectrum and rolloff factor $r = 0.5$, which has already been discussed on the page Trapezoidal low-pass filter of the book "Linear Time Invariant Systems".
First Nyquist criterion in the frequency domain
Harry Nyquist formulated the condition for a intersymbol interfering free detection not only for the time domain, but in 1928 he also gave the corresponding criterion in the frequency domain.
$\text{First Nyquist criterion:}$ If the spectrum $G_d(f)$ of the basic detection pulse $g_d(t)$ fulfills the condition
- $$\sum \limits_{\it k = -\infty}^{+\infty} G_d \left ( f - \frac{k}{T} \right)= g_0 \cdot T = {\rm const.} \hspace{0.05cm}, $$
then $g_d(t)$ is a Nyquist pulse
- with equidistant zero crossings at the times $\nu \cdot T$ for $\nu \ne 0$ and
- the amplitude $g_d(t = 0) = g_0$.
Note: The proof follows on the next page.
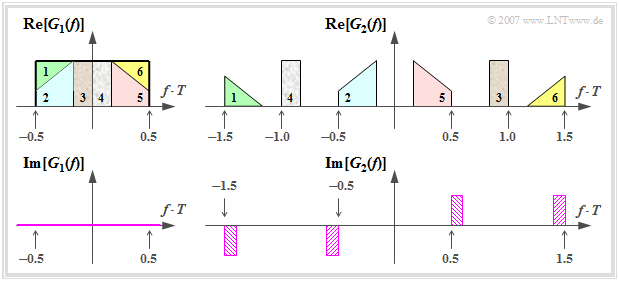
$\text{Example 2:}$ Sketched are two Nyquist spectra $G_1(f)$ and $G_2(f)$, which are composed of rectangular and triangular segments:
- The purely real spectrum sketched on the left
- $$G_1(f) \hspace{-0.05cm}=\hspace{-0.05cm} \left\{ \begin{array}{c} g_0 \cdot T \\ 0 \\ \end{array} \right. \begin{array}{*{1}c} \text{für} \\ \text{für} \\ \end{array}\begin{array}{*{20}c} \vert f \vert \hspace{-0.08cm}<\hspace{-0.08cm} {1}/(2T), \\ \vert f \vert \hspace{-0.08cm}>\hspace{-0.08cm} {1}/(2T) \\ \end{array}$$
- satisfies the condition formulated above with the smallest possible bandwidth. However, the associated Nyquist pulse $g_1(t) = g_0 \cdot {\rm si}(\pi \cdot t/T)$ decays very slowly, asymptotically with $1/t$.
- The real part of the spectrum $G_2(f)$ shown on the upper right was constructed from the rectangular spectrum $G_1(f)$ by shifting parts $1/T$ to the right or left.
$G_2(f)$ is also a Nyquist spectrum because of
- $$\sum \limits_{\it k = -\infty}^{+\infty} {\rm Re}\big[G_2 \left ( f - {k}/{T} \right)\big]= g_0 \cdot T \hspace{0.05cm}, \hspace{0.5cm}\sum \limits_{\it k = -\infty}^{+\infty} {\rm Im}\left[G_2 \big ( f - {k}/{T} \right)\big]= 0.$$
- In the imaginary part, the respective equally shaded parts, each $2/T$ apart, cancels out.
- However, the specification of the corresponding Nyquist pulse $g_2(t)$ is very complicated.
Proof of the first Nyquist criterion
(1) We start from the first Nyquist condition in the time domain:
- $$g_{\hspace{0.05cm}\rm Nyq}(\nu T) = \left\{ \begin{array}{c} g_0 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{for} } \\ {\rm{for} } \\ \end{array}\begin{array}{*{20}c} \nu = 0 \hspace{0.05cm}, \\ \nu \ne 0 \hspace{0.1cm}. \\ \end{array}$$
(2) Thus, from the second Fourier integral, we obtain for $\nu \ne 0$:
- $$g_{\hspace{0.05cm}\rm Nyq}(\nu T) = \int_{-\infty}^{+\infty}G_{\rm Nyq}(f) \cdot {\rm e}^{ \hspace{0.05cm}{\rm j} \hspace{0.05cm}2 \pi f \hspace{0.05cm}\nu \hspace{0.05cm}T}\,{\rm d} f = 0 \hspace{0.05cm}.$$
(3) Decomposing the Fourier integral into partial integrals of width $1/T$, the conditional equations are:
- $$\sum_{k = -\infty}^{+\infty} \hspace{0.2cm} \int_{(k-1/2)/T}^{(k+1/2)/T}G_{\rm Nyq}(f) \cdot {\rm e}^{ \hspace{0.05cm}{\rm j} \hspace{0.05cm}2 \pi f \hspace{0.05cm}\nu \hspace{0.05cm}T}\,{\rm d} f = 0 \hspace{0.05cm}.$$
(4) With the substitution $f\hspace{0.08cm}' = f + k/T$ it follows:
- $$\sum_{k = -\infty}^{+\infty} \hspace{0.2cm} \int_{-1/(2T)}^{1/(2T)}G_{\rm Nyq}(f\hspace{0.08cm}' - \frac{k}{T} ) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}2 \pi \hspace{0.05cm} \cdot \hspace{0.05cm} (f\hspace{0.08cm}'- k/T) \hspace{0.05cm} \cdot \hspace{0.05cm}\nu \hspace{0.05cm}T}\,{\rm d} f \hspace{0.08cm}' = 0 \hspace{0.05cm}.$$
(5) For all integer values of $k$ and $\nu$ holds:
- $${\rm e}^{ - {\rm j} \hspace{0.05cm}2 \pi \hspace{0.05cm} k \hspace{0.05cm} \nu } = 1 \hspace{0.4cm} \Rightarrow \hspace{0.4cm}\sum_{k = - \infty}^{+\infty} \hspace{0.2cm} \int_{- 1/(2T)}^{1/(2T)}G_{\rm Nyq}(f\hspace{0.08cm}' - \frac{k}{T} ) \cdot {\rm e}^{ {\rm j} \hspace{0.05cm}2 \pi \hspace{0.02cm}f\hspace{0.08cm}' \hspace{0.02cm} \nu \hspace{0.05cm}T}\,{\rm d} f \hspace{0.08cm}' = 0 \hspace{0.05cm}.$$
(6) Swapping summation and integration and renaming $f\hspace{0.08cm}'$ to $f$, it further follows:
- $$\int_{-1/(2T)}^{1/(2T)}\hspace{0.2cm} \sum_{k = - \infty}^{+\infty} G_{\rm Nyq}(f - \frac{k}{T} ) \cdot {\rm e}^{ {\rm j} \hspace{0.05cm}2 \pi \hspace{0.02cm}f \hspace{0.02cm} \nu \hspace{0.05cm}T}\,{\rm d} f = 0 \hspace{0.05cm}.$$
(7) This requirement can be satisfied for all $\nu \ne 0$ only if the infinite sum is independent of $f$, i.e., has a constant value:
- $$\sum_{k = -\infty}^{+\infty} G_{\rm Nyq}(f - \frac{k}{T} ) = K_{\rm Nyq} \hspace{0.05cm}.$$
(8) From the penultimate equation, we obtain simultaneously for $\nu = 0$:
- $$\int_{-1/(2T)}^{1/(2T)}\hspace{0.2cm} \sum_{k = -\infty}^{+\infty} G_{\rm Nyq}(f - \frac{k}{T} ) \,{\rm d} f = K_{\rm Nyq} \cdot \frac{1}{T} = g_0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}K_{\rm Nyq} = g_0 \cdot T \hspace{0.05cm}.$$
1/T Nyquist spectra
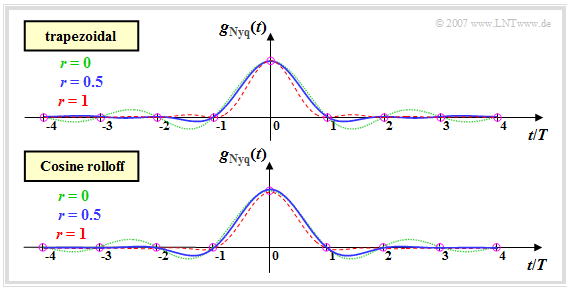
Nyquist spectra which are limited to the frequency range $-1/T \le f \le +1/T$ and are coherent are of particular importance for digital signal transmission. The diagram shows the trapezoidal characteristic and the cosine rolloff characteristic, which are two variants in this respect.
The same applies to both Nyquist spectra:
- The rolloff occurs between the two corner frequencies $f_1$ and $f_2$ point-symmetrically about the Nyquist frequency $f_{\rm Nyq} = (f_1+f_2)/2$. That is, for $0 \le f \le f_{\rm Nyq}$:
- $$G_{\rm Nyq}(f_{\rm Nyq}+f) + G_{\rm Nyq}(f_{\rm Nyq}-f) = g_0 \cdot T \hspace{0.05cm}.$$
- For all frequencies $|f| \le f_1$, $G_{\rm Nyq}(f)$ is constantly equal to $g_0 \cdot T$ and for $|f| \ge f_2$ it is identically zero. In the range between $f_1$ and $f_2$ holds:
- $$\frac{G_{\rm Nyq}(f)}{g_0 \cdot T } = \left\{ \begin{array}{c} \frac{f_2 - |f|}{f_2 -f_1 } \\ \\ \cos^2( \frac{\pi}{2}\cdot \frac{f_2 - |f|}{f_2 -f_1 }) \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{at \hspace{0.15cm}trapezoidal}\hspace{0.05cm},} \\ \\ {\rm{\rm{at \hspace{0.15cm}cosine \hspace{0.15cm}rolloff}}\hspace{0.05cm}.} \\ \end{array}$$
- To parameterize the slope, we use the rolloff factor $r$, which can take values between $0$ and $1$ (including these limits):
- $$r = \frac{f_2 -f_1 } {f_2 +f_1 } \hspace{0.05cm}.$$
- For $r = 0$ ⇒ $f_1 = f_2 = f_{\rm Nyq}$ we obtain the (green–dotted) rectangular Nyquist spectrum.
- The rolloff factor $r = 1$ ⇒ $f_1 = 0, \ f_2 = 2 f_{\rm Nyq}$ stands for a triangular and a $\cos^2$ spectrum, respectively – depending on which of the two basic structures shown above one assumes. These frequency curves are shown in red dashed lines.
Note: In the literature, the rolloff factor is sometimes also referred to as $\alpha$ ("alpha").
Time domain description of the 1/T Nyquist spectra
Let us now consider the Nyquist pulses. For the trapezoidal spectrum with rolloff factor $r$, we obtain:
- $$g_{_{\rm Trapezoid}} ( t )= g_0 \cdot {\rm si} \left ( \frac{\pi \cdot t}{T}\right)\cdot {\rm si} \left ( \frac{\pi \cdot r \cdot t}{T}\right) \hspace{0.5cm}{\rm with }\hspace{0.5cm}{\rm si}(x) = {\rm sin}(x)/x .$$
In contrast, the Fourier inverse transform of the cosine rolloff spectrum (short: CRO spectrum) yields:
- $$g_{_{\rm CRO}} ( t )= g_0 \cdot {\rm si} \left ( \frac{\pi \cdot t}{T}\right)\cdot \frac{\cos(\pi \cdot r \cdot t/T)}{1 - (2 \cdot r \cdot t/T)^2 } \hspace{0.3cm}{\rm with }\hspace{0.3cm}{\rm si}(x) = {\rm sin}(x)/x.$$
These two Nyquist pulses can be viewed using the interactive applet Frequency & Impulse Responses $($with the setting $ \Delta \cdot f = 1)$, illustrating the influence of the rolloff factor $r$.
The following upper diagram shows the Nyquist pulse with trapezoidal spectrum for different rolloff factors. Below is the corresponding time course for the cosine rolloff spectrum. One can see:
- The smaller the rolloff factor $r$, the slower the decay of the Nyquist pulse. This statement is true for both the trapezoidal and cosine rolloff spectra.
- In the limiting case $r \to 0$, both cases yield the rectangular Nyquist spectrum and the $\rm si$–shaped Nyquist pulse, which decays asymptotically with $1/t$ (thin green curves).
- For an average rolloff $(r \approx 0.5)$, the first overshoots are smaller for the trapezoidal spectrum than for the CRO spectrum, because here the Nyquist slope is flatter for a given $r$ (blue curves).
- With the rolloff factor $r = 1$, the trapezoid becomes a triangle in the frequency domain and the CRO spectrum becomes the cosine–square spectrum. In the diagrams on the last page these spectral functions are drawn in red.
- With $r = 1$ the asymptotic decay of the upper time function (according to the trapezoidal spectrum) occurs with $1/t^2$ and the decay of the lower time function (according to the CRO spectrum) with $1/t^3$.
- This means: After a longer time, the CRO Nyquist pulse has settled better than the trapezoidal Nyquist pulse.
Second Nyquist criterion
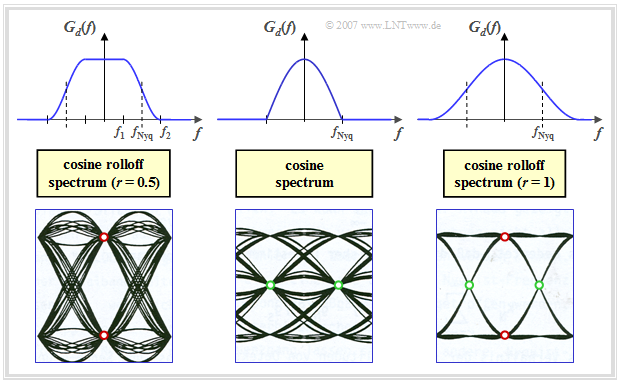
Before the exact mathematical definition, the significance of the second Nyquist criterion for the evaluation of a digital system is illustrated by means of diagrams. The diagram shows three examples of Nyquist systems:
- at the top, the Nyquist spectrum $G_d(f)$,
- below the corresponding eye diagram referring to the third main chapter.
Interpretation:
- The diagram on the left shows the eye diagram of a Nyquist system with cosine rolloff characteristic, where the rolloff factor $r= 0.5$ was chosen. Since the first Nyquist criterion is fulfilled here (there is point symmetry around the Nyquist frequency $f_{\rm Nyq}$, the largest possible value for the vertical eye opening at time $t = 0$ is $2 \cdot g_d(0)$. All eye lines pass through one of the two points marked in red at time $t = 0$ ⇒ the eye is vertically maximally open.
- The middle spectrum does not show any symmetry with respect to the rolloff, so that the first Nyquist criterion is not fulfilled here – in contrast to the second one. All eyelines here intersect the time axis at the same times (marked by the green dots), which facilitates, for example, clock recovery by means of a PLL (Phase-Locked Loop ). When the second Nyquist criterion is met, the horizontal eye opening is maximally equal to the symbol duration $T$ ⇒ the eye is maximally open horizontally.
- The right eye diagram illustrates that for the CRO spectrum with $r = 1$, both the first and second Nyquist criteria are satisfied. The Nyquist pulse
- $$g_d ( t )= g_0 \cdot \frac{\pi }{4}\cdot {\rm si} \left ( \frac{\pi \cdot t}{T}\right)\cdot \left [ {\rm si}(\pi \cdot (\frac{t}{T} + \frac{1}{2}) + {\rm si}(\pi \cdot (\frac{t}{T} - \frac{1}{2})\right]$$
- here exhibits the required zero crossings at $t = \pm T$, $t = \pm 1.5T$, $t = \pm 2T$, $t = \pm 2.5T$, ... but not at $t = \pm 0.5T$. The pulse amplitude is $g_d(t = 0) = g_0$. Note: No other pulse satisfies both the first and second Nyquist criteria simultaneously.
$\text{Summary of Nyquist criteria:}$
(1) In memory of the physicist Harry Nyquist we denote a basic detection pulse $g_d( t)$ with the properties
- $$g_d ( t= 0) \ne 0, \hspace{1cm} g_d ( t)= 0 \hspace{0.3cm}{\rm{for} }\hspace{0.3cm} t = \pm T, \pm 2T,\pm 3T,\hspace{0.05cm}\text{...}$$
- as the Nyquist–1 pulse $g_{\hspace{0.05cm}\rm Nyq-1}(t)$. This satisfies the first Nyquist criterion and leads to the maximum vertical eye opening.
(2) A pulse $g_{\hspace{0.05cm}\rm Nyq-2}(t)$ satisfying the second Nyquist criterion must have zero crossings at $t = \pm 1.5T$, $t = \pm 2.5T$, ... have:
- $$g_d ( t= 0.5) \ne 0, \hspace{0.8cm} g_d ( t)= 0 \hspace{0.3cm}{\rm{for} }\hspace{0.3cm} t = \pm 1.5T, \ \pm 2.5T,\ \pm 3.5T,\hspace{0.05cm}\text{...}$$
- Such a Nyquist–2 pulse leads to the maximum horizontal eye opening.
(3) A Nyquist–2 pulse can always be represented as the sum of two Nyquist–1 pulses shifted by $t = \pm T/2$:
- $$g_{\rm Nyq-2} ( t )= g_{\rm Nyq-1} ( t +T/2)+g_{\rm Nyq-1} ( t -T/2)\hspace{0.05cm}.$$
(4) In the frequency domain, the second Nyquist criterion (see [ST85] [1]) is:
- $$\sum_{k = -\infty}^{+\infty} \frac {G_d \left ( f -k/T \right)}{\cos(\pi \cdot f \cdot T - k \cdot \pi)}= {\rm const.}$$
$\text{Example 3:}$ Starting from the Nyquist–1 pulse $g_{\rm Nyq-1}( t )= g_0 \cdot {\rm si}(\pi \cdot t/T)$ the corresponding Nyquist–2 pulse is:
- $$g_{\rm Nyq-2}( t ) = g_0 \cdot \left [ {\rm si}(\pi \cdot \frac{t + T/2}{T}) + {\rm si}(\pi \cdot \frac{t- T/2}{T}) \right] =\frac{2 \cdot g_0}{\pi} \cdot \frac{\cos(\pi \cdot t/T)}{1 - (2 \cdot t/T)^2}\hspace{0.05cm}.$$
- Due to the limitation of the spectrum $G_{\rm Nyq-1}( f)$ to the range $\vert f \vert \le f_{\rm Nyq} = 1/(2T)$, in equation (4) above the sum is limited to the term with $k = 0$ and we obtain:
- $$G_{\rm Nyq-2}(f) = \left\{ \begin{array}{c} g_0 \cdot T \cdot \cos(\pi/2 \cdot f/f_{\rm Nyq}) \\ \\ 0 \\\end{array} \right.\quad \begin{array}{*{1}c} {\rm{for} }\hspace{0.15cm} \vert f \vert < f_{\rm Nyq}\hspace{0.05cm}, \\ \\ {\rm{otherwise} }\hspace{0.05cm}. \\ \end{array}$$
- This frequency response and the corresponding eye diagram is sketched in the middle column of the above diagram.
- From the bottom diagram, one can clearly see the fulfillment of the second Nyquist criterion.
Exercises for the chapter
Exercise 1.4: Nyquist Criteria
Exercise 1.4Z: Complex Nyquist Spectrum
Exercise 1.5: Cosine-Square Spectrum
References
- ↑ Söder, G.; Tröndle, K.: Digitale Übertragungssysteme - Theorie, Optimierung & Dimensionierung der Basisbandsysteme. Berlin – Heidelberg: Springer, 1985.