Difference between revisions of "Exercise 2.4Z: Characteristics Measurement"
m (Text replacement - "Category:Exercises for Linear and Time-Invariant Systems" to "Category:Linear and Time-Invariant Systems: Exercises") |
|||
| (7 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Linear_and_Time_Invariant_Systems/Nonlinear_Distortion |
}} | }} | ||
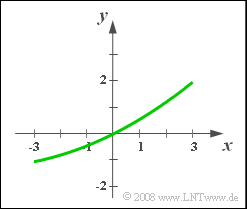
| − | [[File:P_ID898__LZI_Z_2_4.png|right|frame| | + | [[File:P_ID898__LZI_Z_2_4.png|right|frame|Given characteristic $y = g(x)$]] |
| − | + | It is known that the characteristic curve can be represented as follows for a nonlinear system: | |
:$$y(t) = c_1 \cdot x(t) + c_2 \cdot x^2(t).$$ | :$$y(t) = c_1 \cdot x(t) + c_2 \cdot x^2(t).$$ | ||
| − | + | Since the distortions are nonlinear no frequency response $H(f)$ can be given. | |
| − | + | To determine the dimensionless coefficient $c_1$ as well as the quadratic coefficient $c_2$ different rectangular pulses $x(t)$ – characterized by the amplitude $A_x$ and the width $T_x$ – are now applied to the input and the pulse amplitude $A_y$ at the output is measured in each case. | |
| − | + | The first three trials generate the following values: | |
* $A_x = 1 \ {\rm V}, \; \; T_x = 8 \ {\rm ms}$ : $A_y = 0.55 \ {\rm V}$, | * $A_x = 1 \ {\rm V}, \; \; T_x = 8 \ {\rm ms}$ : $A_y = 0.55 \ {\rm V}$, | ||
* $A_x = 2 \ {\rm V}, \; \; T_x = 4 \ {\rm ms}$ : $A_y = 1.20 \ {\rm V}$, | * $A_x = 2 \ {\rm V}, \; \; T_x = 4 \ {\rm ms}$ : $A_y = 1.20 \ {\rm V}$, | ||
| Line 17: | Line 17: | ||
| − | + | For the subtasks '''(3)''' and '''(4)''' let the input signal $x(t)$ be a harmonic oscillation because only for such an oscillation a distortion factor can be specified. | |
| − | + | In contrast, a triangular pulse with amplitude $A_x = 3 \ {\rm V}$ and the one-sided pulse duration $T_x = 2 \ {\rm ms}$ is considered for the subtask '''(5)''' : | |
:$$x(t) = A_x \cdot ( 1 - {|t|}/{T_x}) $$ | :$$x(t) = A_x \cdot ( 1 - {|t|}/{T_x}) $$ | ||
| Line 26: | Line 26: | ||
| − | + | ''Please note:'' | |
| − | + | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Nonlinear_Distortion|Nonlinear Distortions]]. | |
| − | |||
| − | |||
| − | '' | ||
| − | * | ||
| − | * | + | *The following abbreviations are used in the formulation of the questions: |
:$$y_1(t) = c_1 \cdot x(t), \hspace{0.5cm} y_2(t) = c_2 \cdot | :$$y_1(t) = c_1 \cdot x(t), \hspace{0.5cm} y_2(t) = c_2 \cdot | ||
x^2(t).$$ | x^2(t).$$ | ||
| Line 39: | Line 35: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {A rectangular pulse $x(t)$ with amplitude $A_x$ and duration $T_x$ is applied to the input. <br>Which statements hold for the output pulse $y(t)$? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - The output pulse $y(t)$ is triangular in shape. |
| − | - | + | - The amplitudes at the input and output are the same ⇒ $A_y = A_x$. |
| − | + | + | + The pulse duration is not changed by the system ⇒ $T_y = T_x$. |
| − | { | + | {Compute the first two coefficients of the Taylor series. |
|type="{}"} | |type="{}"} | ||
$c_1 \ = \ $ { 0.5 3% } | $c_1 \ = \ $ { 0.5 3% } | ||
| Line 55: | Line 51: | ||
| − | { | + | {Which distortion factor $K$ is measured with the test signal $x(t) = 1 \hspace{0.08cm} {\rm V} \cdot \cos(\omega_0 \cdot t)$ ? That is: $\underline{A_x = 1\hspace{0.08cm} \rm V}$. |
|type="{}"} | |type="{}"} | ||
$K \ = \ $ { 5 3% } $\ \%$ | $K \ = \ $ { 5 3% } $\ \%$ | ||
| − | { | + | {Which distortion factor $K$ is measured with the test signal $x(t) = 3 \hspace{0.08cm} {\rm V} \cdot \cos(\omega_0 \cdot t)$ ? That is: $\underline{A_x = 3\hspace{0.08cm} \rm V}$. |
|type="{}"} | |type="{}"} | ||
$K \ = \ $ { 15 3% } $\ \%$ | $K \ = \ $ { 15 3% } $\ \%$ | ||
| − | { | + | {Which output pulse $y(t)$ arises as a result when the input pulse is triangular? What are the signal values at $ t = 0$ and $ t = T_x/2$? |
|type="{}"} | |type="{}"} | ||
$y(t = 0) \ = \ $ { 1.95 3% } $\ \rm V$ | $y(t = 0) \ = \ $ { 1.95 3% } $\ \rm V$ | ||
| Line 74: | Line 70: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>Proposed solution 3</u> is the only correct one: |
| − | * | + | *If the input pulse $x(t)$ is rectangular, then $x^2(t)$ is also a rectangle with height $A_x^2$ between $0$ and $T_x$, outside zero. |
| − | * | + | *The overall output signal $y(t)$ is thus also rectangular with the amplitude |
:$$A_y= c_1 \cdot A_x + c_2 \cdot A_x^2 .$$ | :$$A_y= c_1 \cdot A_x + c_2 \cdot A_x^2 .$$ | ||
| − | * | + | *The following holds for the pulse duration: $T_y = T_x$. |
| − | '''(2)''' | + | '''(2)''' The following system of linear equations can be specified with the first two sets of parameters: |
:$$c_1 \cdot 1\,{\rm V} + c_2 \cdot (1\,{\rm V})^2 = 0.55\,{\rm | :$$c_1 \cdot 1\,{\rm V} + c_2 \cdot (1\,{\rm V})^2 = 0.55\,{\rm | ||
V},$$ | V},$$ | ||
| Line 90: | Line 86: | ||
V}.\hspace{0.05cm}$$ | V}.\hspace{0.05cm}$$ | ||
| − | * | + | *The following is obtained by multiplying the first equation by $-2$ and adding the two equations: |
:$$c_2 \cdot 2\,{\rm V}^2 = 0.1\,{\rm | :$$c_2 \cdot 2\,{\rm V}^2 = 0.1\,{\rm | ||
V} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} c_2 \hspace{0.15cm}\underline{= 0.05\cdot{1/\rm | V} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} c_2 \hspace{0.15cm}\underline{= 0.05\cdot{1/\rm | ||
V}}.$$ | V}}.$$ | ||
| − | * | + | *The linear coefficient is thus $c_1 \hspace{0.15cm}\underline{= 0.5}.$ |
| − | * | + | *The third set of parameters can be used to verify the result: |
:$$c_1 \cdot 3\,{\rm V} + c_2 \cdot (3\,{\rm V})^2 = 0.5 \cdot 3\,{\rm | :$$c_1 \cdot 3\,{\rm V} + c_2 \cdot (3\,{\rm V})^2 = 0.5 \cdot 3\,{\rm | ||
V}+ 0.05 \ {1}/{\rm V}\cdot 9\,{\rm V}^2 = 1.95\,{\rm | V}+ 0.05 \ {1}/{\rm V}\cdot 9\,{\rm V}^2 = 1.95\,{\rm | ||
| Line 102: | Line 98: | ||
| − | '''(3)''' | + | '''(3)''' The specification of a distortion factor requires the use of a harmonic oscillation at the input. |
| − | * | + | *If $X_+(f) = 1 \ {\rm V} \cdot \delta (f - f_0)$ holds, then the spectrum of the analytic signal at the output is: |
:$$ Y_{+}(f)={c_2}/{2}\cdot A_x^2 \cdot \delta(f) + c_1\cdot A_x \cdot \delta(f- f_0)+ {c_2}/{2}\cdot A_x^2 \cdot \delta(f- 2 f_0). $$ | :$$ Y_{+}(f)={c_2}/{2}\cdot A_x^2 \cdot \delta(f) + c_1\cdot A_x \cdot \delta(f- f_0)+ {c_2}/{2}\cdot A_x^2 \cdot \delta(f- 2 f_0). $$ | ||
| − | * | + | *The Dirac function at $f = 0$ follows from the trigonometric transformation $\cos^2(\alpha) = 1/2 + 1/2 \cdot \cos(\alpha).$ |
| − | * | + | *With $A_1 = c_1 \cdot A_x = 0.5 \ {\rm V} $ and $A_2 = (c_2/2) \cdot A_x^2 = 0.025 \ {\rm V}^2 $ the following is thus obtained for the distortion factor: |
:$$K= \frac{A_2}{A_1}= \frac{c_2/2 \cdot A_x}{c_1 }= \frac{0.025}{0.5} \hspace{0.15cm}\underline{= 5 \%}.$$ | :$$K= \frac{A_2}{A_1}= \frac{c_2/2 \cdot A_x}{c_1 }= \frac{0.025}{0.5} \hspace{0.15cm}\underline{= 5 \%}.$$ | ||
| − | '''(4)''' | + | '''(4)''' According to the solution of the last subtask $K$ is proportional to $A_x$. Therefore, one now obtains $K \hspace{0.15cm}\underline{= 15 \%}.$ |
| − | '''(5)''' | + | '''(5)''' Now the output signal is: |
:$$y(t)= c_1\cdot A_x \cdot \left( 1 - {|\hspace{0.05cm}t\hspace{0.05cm}|}/{T_x}\right) +\hspace{0.1cm} | :$$y(t)= c_1\cdot A_x \cdot \left( 1 - {|\hspace{0.05cm}t\hspace{0.05cm}|}/{T_x}\right) +\hspace{0.1cm} | ||
{c_2}\cdot A_x^2 \cdot \left( 1 - {|\hspace{0.05cm}t\hspace{0.05cm}|}/{T_x}\right)^2.$$ | {c_2}\cdot A_x^2 \cdot \left( 1 - {|\hspace{0.05cm}t\hspace{0.05cm}|}/{T_x}\right)^2.$$ | ||
| − | * | + | *The following values occur at times $t = 0$ and $t = T_x/2$: |
:$$y(t=0) = c_1\cdot A_x + {c_2}\cdot A_x^2 \hspace{0.15cm}\underline{= 1.95\,{\rm | :$$y(t=0) = c_1\cdot A_x + {c_2}\cdot A_x^2 \hspace{0.15cm}\underline{= 1.95\,{\rm | ||
V}},$$ | V}},$$ | ||
| Line 131: | Line 127: | ||
| − | [[Category:Linear and Time-Invariant Systems: Exercises|^2.2 | + | [[Category:Linear and Time-Invariant Systems: Exercises|^2.2 Nonlinear Distortions^]] |
Latest revision as of 15:29, 1 October 2021
It is known that the characteristic curve can be represented as follows for a nonlinear system:
- $$y(t) = c_1 \cdot x(t) + c_2 \cdot x^2(t).$$
Since the distortions are nonlinear no frequency response $H(f)$ can be given.
To determine the dimensionless coefficient $c_1$ as well as the quadratic coefficient $c_2$ different rectangular pulses $x(t)$ – characterized by the amplitude $A_x$ and the width $T_x$ – are now applied to the input and the pulse amplitude $A_y$ at the output is measured in each case.
The first three trials generate the following values:
- $A_x = 1 \ {\rm V}, \; \; T_x = 8 \ {\rm ms}$ : $A_y = 0.55 \ {\rm V}$,
- $A_x = 2 \ {\rm V}, \; \; T_x = 4 \ {\rm ms}$ : $A_y = 1.20 \ {\rm V}$,
- $A_x = 3 \ {\rm V}, \; \; T_x = 2 \ {\rm ms}$ : $A_y = 1.95 \ {\rm V}$.
For the subtasks (3) and (4) let the input signal $x(t)$ be a harmonic oscillation because only for such an oscillation a distortion factor can be specified.
In contrast, a triangular pulse with amplitude $A_x = 3 \ {\rm V}$ and the one-sided pulse duration $T_x = 2 \ {\rm ms}$ is considered for the subtask (5) :
- $$x(t) = A_x \cdot ( 1 - {|t|}/{T_x}) $$
Please note:
- The exercise belongs to the chapter Nonlinear Distortions.
- The following abbreviations are used in the formulation of the questions:
- $$y_1(t) = c_1 \cdot x(t), \hspace{0.5cm} y_2(t) = c_2 \cdot x^2(t).$$
Questions
Solution
- If the input pulse $x(t)$ is rectangular, then $x^2(t)$ is also a rectangle with height $A_x^2$ between $0$ and $T_x$, outside zero.
- The overall output signal $y(t)$ is thus also rectangular with the amplitude
- $$A_y= c_1 \cdot A_x + c_2 \cdot A_x^2 .$$
- The following holds for the pulse duration: $T_y = T_x$.
(2) The following system of linear equations can be specified with the first two sets of parameters:
- $$c_1 \cdot 1\,{\rm V} + c_2 \cdot (1\,{\rm V})^2 = 0.55\,{\rm V},$$
- $$c_1 \cdot 2\,{\rm V} + c_2 \cdot (2\,{\rm V})^2 = 1.20\,{\rm V}.\hspace{0.05cm}$$
- The following is obtained by multiplying the first equation by $-2$ and adding the two equations:
- $$c_2 \cdot 2\,{\rm V}^2 = 0.1\,{\rm V} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} c_2 \hspace{0.15cm}\underline{= 0.05\cdot{1/\rm V}}.$$
- The linear coefficient is thus $c_1 \hspace{0.15cm}\underline{= 0.5}.$
- The third set of parameters can be used to verify the result:
- $$c_1 \cdot 3\,{\rm V} + c_2 \cdot (3\,{\rm V})^2 = 0.5 \cdot 3\,{\rm V}+ 0.05 \ {1}/{\rm V}\cdot 9\,{\rm V}^2 = 1.95\,{\rm V}.$$
(3) The specification of a distortion factor requires the use of a harmonic oscillation at the input.
- If $X_+(f) = 1 \ {\rm V} \cdot \delta (f - f_0)$ holds, then the spectrum of the analytic signal at the output is:
- $$ Y_{+}(f)={c_2}/{2}\cdot A_x^2 \cdot \delta(f) + c_1\cdot A_x \cdot \delta(f- f_0)+ {c_2}/{2}\cdot A_x^2 \cdot \delta(f- 2 f_0). $$
- The Dirac function at $f = 0$ follows from the trigonometric transformation $\cos^2(\alpha) = 1/2 + 1/2 \cdot \cos(\alpha).$
- With $A_1 = c_1 \cdot A_x = 0.5 \ {\rm V} $ and $A_2 = (c_2/2) \cdot A_x^2 = 0.025 \ {\rm V}^2 $ the following is thus obtained for the distortion factor:
- $$K= \frac{A_2}{A_1}= \frac{c_2/2 \cdot A_x}{c_1 }= \frac{0.025}{0.5} \hspace{0.15cm}\underline{= 5 \%}.$$
(4) According to the solution of the last subtask $K$ is proportional to $A_x$. Therefore, one now obtains $K \hspace{0.15cm}\underline{= 15 \%}.$
(5) Now the output signal is:
- $$y(t)= c_1\cdot A_x \cdot \left( 1 - {|\hspace{0.05cm}t\hspace{0.05cm}|}/{T_x}\right) +\hspace{0.1cm} {c_2}\cdot A_x^2 \cdot \left( 1 - {|\hspace{0.05cm}t\hspace{0.05cm}|}/{T_x}\right)^2.$$
- The following values occur at times $t = 0$ and $t = T_x/2$:
- $$y(t=0) = c_1\cdot A_x + {c_2}\cdot A_x^2 \hspace{0.15cm}\underline{= 1.95\,{\rm V}},$$
- $$y(t=T_x/2) = c_1\cdot A_x \cdot {1}/{2} + \hspace{0.1cm}{c_2}\cdot A_x^2 \cdot {1}/{4}= 0.75\,{\rm V}+ 0.1125\,{\rm V} \hspace{0.15cm}\underline{ = 0.8625\,{\rm V}}.$$