Envelope Demodulation

1. Modulation Methods
2. Amplitudenmodulation und AM–Demodulation
3. Envelope Demodulation

• Previous page
• Next page

• Previous page
• Next page

Functionality under ideal conditions

Wie first assume the following conditions:

• Let the source signal  $q(t)$  be free of a DC component and limited in magnitude to  $q_{\rm max}$ .
• The transmission is based on the modulation method „DSB–AM with carrier”. 
• For simplicity of representation, the carrier phase is set to  $\mathbf{ϕ_{\rm T} } = 0$  without restricting generality:

$$s(t) = \left(q(t) + A_{\rm T}\right) \cdot \cos (\omega_{\rm T}\cdot t )\hspace{0.05cm}.$$

• Let the modulation depth be $m ≤ 1$.  Therefore, from the definition $m = q_{\rm max}/A_{\rm T}$  it also follows that  $q(t) + A_{\rm T} ≥ 0$.
• Let the channel be ideal, that is, there is no distortion, no attenuation, no delay, and no (noise) interference.
• Thus, when  $H_{\rm K}(f) = 1$  and  $n(t) \equiv 0$  we get

$$r(t) = s(t) = a(t) \cdot \cos (\omega_{\rm T}\cdot t )\hspace{0.05cm}$$

for the received signal.

• In this equation,  $a(t)$  describes the   envelope of  $r(t)$.  The phase function is  $\mathbf{ϕ}(t) = 0$.

$\text{Definition:}$   An   envelope demodulator  detects the envelope  $a(t)$  of its input signal  $r(t)$  and outputs it as a sink signal after eliminating the DC component  $A_{\rm T}$ :

$$v(t) = a(t) - A_{\rm T}\hspace{0.05cm}.$$

The removal of the DC component  $A_{\rm T}$  can be realized, for example, by a high-pass filter that allows all frequencies to pass unimpeded except for $f = 0$ .

• If all the above conditions are met, then $v(t) = q(t)$ holds.
• This means that an ideal message communication system can certainly be realized with an (ideal) envelope demodulator.

Signal waveforms illustrating envelope demodulation

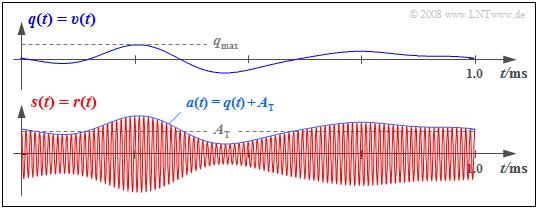
$\text{Example 1:}$   In the graph, the received signal  $r(t) = s(t)$  is shown below, and is based on "DSB–AM with carrier” $($modulation depth  $m = 0.5)$.

• The envelope  $a(t)$  to be evaluated by the envelope demodulator is equal to the sum of the source signal  $q(t)$  and the DC component  $A_{\rm T}$ added at the transmitter.

•  $v(t) = q(t)$ holds for the demodulator output signal after removing the DC component  $A_{\rm T}$  with a high-pass filter, assuming that the source signal  $q(t)$  did not include a DC component.   Such a component would (wrongly) also be removed by the high-pass filter.

Realizing an envelope demodulator

rechts

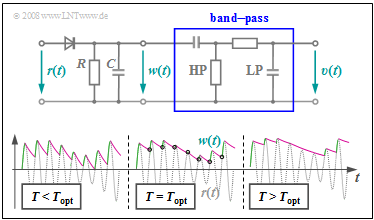
The adjacent graph shows:

• above, a simple possible realization of the envelope demodulator above,
• below, the signals  $r(t)$  and  $w(t)$  to illustrate the principle.

First, consider the middle signal section denoted by  $T = T_{\rm opt}$ .

The first circuit section – consisting of a diode and a parallel connection of a resistor  $R$  and a capacitance $C$  – performs the following tasks:

• If the (light) grey signal $r(t)$ is larger than the voltage  $r(t)$  at  $R$  and  $C$, the diode conducts,  $w(t) = r(t)$  holds, and the capacitance $C$ is charged. In these regions, the signal  $w(t)$  is drawn in green.
• If  $r(t) < w(t)$ , as it does at the times marked in purple, the diode blocks and the capacitance discharges through resistor  $R$. The signal  $w(t)$  decays exponentially with time constant  $T = R · C$ .
• From the times marked with circles,  $r(t) > w(t)$  holds again and the capacitance is recharged. It can be seen from the sketch that  $w(t)$  "approximately" matches the envelope  $a(t)$ .

$\text{Design criteria:}$  

• The deviations between the envelope approximation  $w(t)$  and its nominal function  $a(t)$  decrease the larger the carrier frequency  $f_{\rm T}$  is compared to the bandwidth  $B_{\rm NF}$  of the low frequency message signal. As a guideline,  $f_{\rm T} ≥ 100 · B_{\rm NF}$  is often given.
• At the same time, the time constant  $T$  of the RC –parallel resonant circuit should always be much larger than  $1/f_{\rm T}$  and much smaller than  $1/B_{\rm NF}$ . A good compromise is the geometric mean between the two limits:

$$1/f_{\rm T}\hspace{0.1cm} \ll \hspace{0.1cm} T \hspace{0.1cm} \ll \hspace{0.1cm} 1/B_{\rm NF} \hspace{0.05cm}, \hspace{2cm} T_{\rm opt} = {1}/{\sqrt{f_{\rm T} \cdot B_{\rm NF} } } \hspace{0.05cm}.$$

• If the time constant  $T$  is too small, as in the left area of the sketch above, the capacitor will always discharge too quickly and the deviation  $w(t) \ – \ a(t)$  will be unnecessarily large.
• Also, too large a value  $T > T_{\rm opt}$  will result in deterioration, as shown in the right signal detail. In this case,  $w(t)$  can no longer follow the envelope  $a(t)$ .

$\text{Example 2:}$   For a LF-bandwidth of  $5 \ \rm kHz$ , the carrier frequency should be at least  $500 \ \rm kHz$ .

• The time constant  $T$  must be much larger than  $1/f_{\rm T} = 2 \ \rm µ s$  and at the same time much smaller than  $1/B_{\rm NF} = 200 \ \rm µ s $.
• The optimal value according to the compromise formula is thus:

$$T_{\rm opt} = 1/\sqrt{ 5 \cdot 10^5 \ {\rm Hz} \cdot 5 \cdot 10^3 \ {\rm Hz} } = 20 \ \rm µ s \hspace{0.05cm}.$$

Representation of an envelope demodulator in the frequency domain.

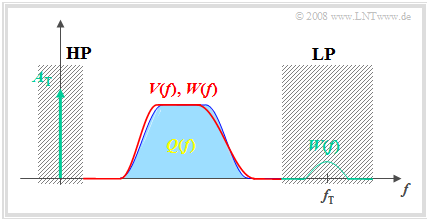
The graph on the right is intended to illustrate the operation of the envelope demodulator in the frequency domain. The spectrum  $W(f)$  of the signal  $w(t)$  at the RC parallel circuit differs from the spectrum  $Q(f)$  of the source signal as follows:

• Due to the carrier signal  $z(t)$  added at the transmitter, the spectral function  $W(f)$  includes a Dirac line at  $f = 0$  with weight  $A_{\rm T}$  (carrier amplitude).
• $W(f)$  also exhibits spectral components in the region around the carrier frequency  $f_{\rm T}$ , which can be explained by the jagged time course of  $w(t)$  (see the first graph in this section).
•  $W(f)$  also differs only slightly from  $Q(f)$  in the LF domain. Here, the error gets smaller as the carrier frequency increases compared to the AF bandwidth.

The first two signal distortions are eliminated by the high-pass and low-pass filters, which together produce a bandpass. However, there also remains a slight deviation between the sink signal  $v(t)$  and the source signal  $q(t)$  in the interesting range  $0 < f < B_{\rm NF}$ , as shown by comparing the output spectrum  $V(f)$  plotted in red and the input spectrum  $Q(f)$  plotted in blue.

Why envelope demodulation fails for   $m > 1$ 

Envelope demodulation when   $m < 1$  (above) and  $m > 1$  (below)

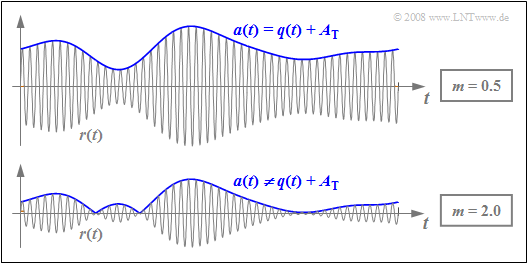
The graph shows the DSB-AM signals for  $m = 0.5$  and  $m = 2$. 

From this picture one can recognise the following differences:

• For a modulation depth  $m ≤ 1$  the envelope of the bandpass signal is characterised by:

$$a(t) = q(t) + A_{\rm T}\hspace{0.05cm}.$$

Here, an ideal demodulation is possible with an envelope demodulator   ⇒ $v(t) = q(t)$, if we ignore unavoidable noise.

• In contrast, when  $m > 1$ , the following relationship holds:

$$a(t) = {q(t) + A_{\rm T} }\hspace{0.05cm}.$$

• Here, envelope demodulation always leads to  nonlinear distortions.
• The sink signal  $v(t)$  now includes new frequencies, which were not present in $q(t)$ .
• For the DC component(expected value) of the envelope der Hüllkurve gilt in diesem Fall:  

$${\rm E}[a(t)] \ne A_{\rm T}\hspace{0.05cm}.$$

• Da nun anstelle von  $A_{\rm T}$  dieser Gleichanteil  ${\rm E}[a(t)]$  durch den Hochpass entfernt wird, kommt es zusätzlich zu einer Pegelverschiebung.

Description using the equivalent low-pass signal

Especially when the source signal  $q(t)$  can be represented as a sum of several harmonic oscillations, a signal description with the equivalent low-pass signal  ${|r_{\rm TP}(t)|}$  is extremely advantageous. This is described in detail in the book  Signal Representation .

$\text{Please note:}$  If noise/interference is disregarded, the received signal can be written as:

$$r(t) = a(t) \cdot \cos (\omega_{\rm T}\cdot t + \phi(t))\hspace{0.05cm}.$$

This equation is valid for any form of amplitude modulation under different boundary conditions:

• Double sideband (DSB) or single sideband (SSB),
• with or without a carrier,
• ideal channel or linear distorting channel.

In general, the associated equivalent low-pass signal is complex and given as:

$$r_{\rm TP}(t) = a(t) \cdot {\rm e}^{\hspace{0.03cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \phi(t)}\hspace{0.05cm}.$$

The time functions  $a(t)$  and  $ϕ(t)$  contained in the equations are identical for both representations:

• $a(t)$  describes the  envelope  (time-dependent amplitude) of the physical signal  $r(t)$  and the magnitude  $\vert r_{\rm TP}(t) \vert $  of the equivalent LP signal, respectively.  This is detected during envelope demodulation.
• $ϕ(t)$  is the  time-dependent phase.  This function contains all information about the position of the zero crossings of  $r(t)$  and indicates whether an additional phase modulation is effective.

In the case of double sideband amplitude modulation, the following holds for an ideal channel:

• The locus curve – by this we mean the time-dependent representation of the signal  $r_{\rm TP}(t)$  in the complex plane – is a horizontal straight line on the real axis.
• It further follows that the phase function can take only two values:  $0$  and  $π$   $(180^\circ)$ .

• When  $m ≤ 1$ , then  $ϕ(t) ≡ 0$  and envelope demodulation can be applied without distortion.
• When  $m > 1$ , a section of the locus curve lies in the left half-plane  ⇒   nonlinear distortions arise when envelope demodulation is applied.

Locus curves illustrating envelope demodulation

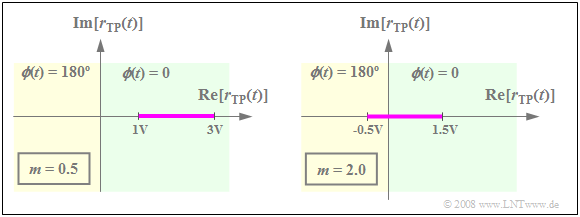
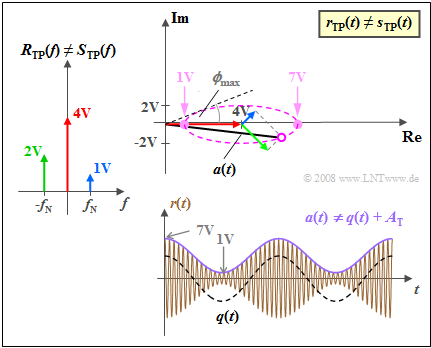
$\text{Example 3:}$   We assume that the source signal  $q(t)$  can take on all values in the range  $±1\ \rm V$ .

• Adding a DC component of  $A_{\rm T} = 2\ \rm V$  results in a DSB-AM with modulation depth  $m = 0.5$, whose locus curve can be seen in the left graph.
• $r_{\rm TP}(t)$  always lies in the right half-plane.  The pointer length changes with the message signal  $q(t)$.

The right-hand graph shows the locus curve for  $A_{\rm T} = 0.5 \ \rm V$   ⇒   $m = 2$.

•  $r_{\rm TP}(t)$  now takes on real values between $-0.5\ \rm V$  and  $1.5\ \rm V$ .
• The envelope demodulator cannot distinguish between positive and negative values   ⇒   nonlinear distortions occur.

The physical signals  $q(t)$,  $r(t)$ and  $v(t)$  corresponding to this example can be found in the graph on the previous page.

Special case of a cosine-shaped message signal

To quantitatively capture the nonlinear distortions due to a modulation depth  $m> 1$ , we assume the following scenario:

Error signal for envelope demodulation

• cosine-shaped source signal:   $q(t) = A_{\rm N} \cdot \cos(\omega_{\rm N} \cdot t);$
• DSB–AM with carrier:   $s(t) = \left ( q(t) + A_{\rm T} \right ) \hspace{-0.05cm}\cdot \hspace{-0.05cm}\cos(\omega_{\rm N} \hspace{-0.05cm}\cdot \hspace{-0.05cm}t),$   $r(t) = s(t);$
• modulation depth:   $m = A_{\rm N}/A_{\rm T} = 1.25;$
• ideal envelope demodulation:   $a(t) = {| q(t) + A_{\rm T}|; $
• elimination of the DC component by low-pass:   $r(t) = a(t) - {\rm E}\big[a(t)\big].$

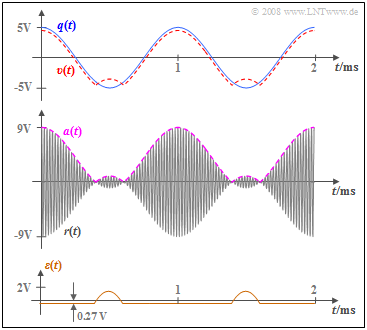
The graph is valid for the signal parameters  $A_{\rm N} = 5 \ \rm V$,  $f_{\rm N} = 2 \ \rm kHz$,  $A_{\rm T} = 4 \ \rm V$  and  $f_{\rm T} = 100\ \rm kHz$.  It shows

• above, the sink signal  $v(t)$  compared to the source signal  $q(t)$,
• in the middle, the received signal  $r(t)$  as well as the envelope curve  $a(t) = {|r(t)|}$,
• below, the error signal  $ε(t) = v(t) \ – \ q(t)$  due to nonlinear distortions.

Based on the graphs, the following statements can be made:

• A comparison of the signals  $q(t)$  and  $a(t)$  reveals, that the envelope  $a(t)$  correctly reproduces the shape of the source signal  $q(t)$  around   $80\%$  of the time in this example.
• However, the maximum of  $a(t)$  is noticeably larger than the maximum of  $q(t)$ due to the added carrier  $A_{\rm T}$ .
• The sink signal  $v(t)$  differs from the envelope curve  $a(t)$  by the expected value  ${\rm Ε}\big[a(t)\big]$, which is removed by the low-pass of the envelope demodulator.
• Since  ${\rm Ε}\big[a(t)\big] = 4.27 \ \rm V$  does not match  $A_{\rm T} = 4 \ \rm V$ ,  $v(t)$  differs from  $q(t)$  by the constant value  $0.27 \ \rm V$, also in the regions where  $a(t)$  is correctly detected.
• Aus dem cosinusförmigen Quellensignal  $q(t)$  wird ein Signal  $v(t)$  mit Oberwellen:

$$v(t) = A_{\rm 1} \cdot \cos(\omega_{\rm N} t ) +A_{\rm 2} \cdot \cos(2\omega_{\rm N} t )+A_{\rm 3} \cdot \cos(3\omega_{\rm N} t )+ \text{...}$$

$$\Rightarrow \hspace{0.3cm}A_{\rm 1} = 4.48\,{\rm V},\hspace{0.3cm}A_{\rm 2} = 0.46\,{\rm V},\hspace{0.3cm}A_{\rm 3} = -0.37\,{\rm V},\hspace{0.3cm} A_{\rm 4} = 0.26\,{\rm V},\hspace{0.1cm}\text{...}$$

• Damit erhält man für die einzelnen Klirrfaktoren sowie den Gesamtklirrfaktor entsprechend den Angaben im Buch  Lineare zeitinvariante Systeme:

$$K_2 ={|A_{\rm 2}|}/{A_{\rm 1}} = 0.102\hspace{0.3cm}K_3 ={|A_{\rm 3}|}/{A_{\rm 1}} = 0.082,\hspace{0.3cm}K_4 = {|A_{\rm 4}|}/{A_{\rm 1}} = 0.058,\hspace{0.1cm}\text{...}$$

$$\Rightarrow \hspace{0.3cm}K = \sqrt{K_2^2 + K_3^2 + K_4^2 +\text{...} } \approx 15 \%.$$

Im Kapitel  Qualitätskriterien  wurde gezeigt, dass damit auch das SNR  $ρ_v = 1/K^2 ≈ 44$  festliegt.  $ρ_v$  $($nicht aber  $K)$  kann zudem auch dann als Qualitätskriterium herangezogen werden, wenn  $q(t)$  mehr als eine Frequenz beinhaltet   ⇒   Herleitung im Buch  Lineare zeitinvariante Systeme.

Berücksichtigung von Kanalverzerrungen

Für die folgenden Betrachtungen setzen wir das Modulationsverfahren „ZSB–AM mit Träger” sowie ein cosinusförmiges Quellensignal  $q(t)$  voraus. Die Amplituden von Nachrichten– und Trägersignal seien  $A_{\rm N} = 4 \ \rm V$  und  $A_{\rm T} = 5 \ \rm V $   ⇒   Modulationsgrad  $m = 0.8$. Damit ist (ideale) Hüllkurvendemodulation prinzipiell anwendbar.

Spektren und Signale zur Verdeutlichung der Hüllkurvendemodulation

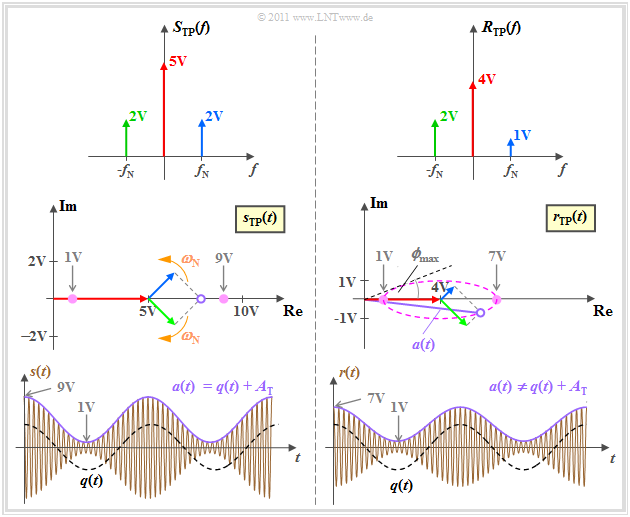
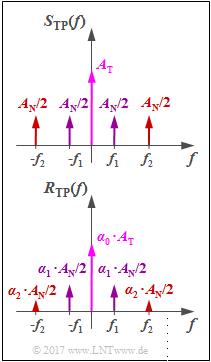
Die Grafik zeigt von oben nach unten

• die Spektren  $S_{\rm TP}(f)$  und  $R_{\rm TP}(f)$  des äquivalenten Tiefpass–Signals, die als reell angenommen werden,
• die äquivalenten Tiefpass–Signale  $s_{\rm TP}(t)$  und  $r_{\rm TP}(t)$  in der komplexen Ebene, und schließlich
• die physikalischen Signale  $s(t)$  und  $r(t)$.

Die linke Bildhälfte zeigt die Senderseite und gibt gleichzeitig die Verhältnisse am Empfänger bei idealem Kanal an.

• Wegen des Modulationsgrades  $m ≤ 1$  erkennt man in der Hüllkurve  $a(t)$  das Quellensignal  $q(t)$.   Demzufolge ist Hüllkurvendemodulation bei gewissen Voraussetzungen ohne Verzerrungen anwendbar, wie im  $\text{Beispiel 4}$  gezeigt wird.

• Die rechte Hälfte berücksichtigt unsymmetrische Verzerrungen durch den Kanal.  Der Träger wird hier mit  $α_{\rm T} = 0.8$  gedämpft, das obere Seitenband sogar mit  $α_{\rm O} = 0.5$.  Nun verläuft die Hüllkurve  $a(t) ≠ q(t) + A_{\rm T}$  nicht mehr cosinusförmig   ⇒   Hüllkurvendemodulation führt hier zu nichtlinearen Verzerrungen wie im  $\text{Beispiel 5}$  gezeigt.

Hüllkurvendemodulation bei idealem Kanal

$\text{Beispiel 4:}$   Es gelte weiterhin  $A_{\rm N} = 4 \ \rm V$  und  $A_{\rm T} = 5 \rm V$   ⇒   Modulationsgrad  $m = 0.8$.

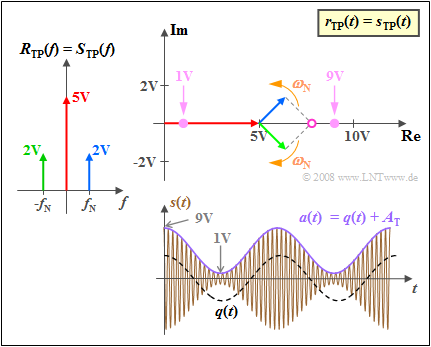
Die Grafik verdeutlicht den Einsatz eines idealen Hüllkurvendemodulators bei idealem Kanal, wobei folgende Identitäten berücksichtigt sind:

$$R_{\rm TP}(f) \hspace{-0.05cm}=\hspace{-0.05cm} S_{\rm TP}(f) \hspace{0.02cm}, \hspace{0.15cm} r_{\rm TP}(t) \hspace{-0.05cm}=\hspace{-0.05cm} s_{\rm TP}(t) \hspace{0.02cm}, \hspace{0.15cm} r(t) \hspace{-0.05cm}=\hspace{-0.05cm} s(t) \hspace{0.02cm}.$$

Man erkennt aus diesen Darstellungen:

• Der den Träger beschreibende rote Zeiger der Länge  $A_{\rm T}$  liegt fest.
• Das obere Seitenband (blau) dreht in mathematisch positiver Richtung, das untere Seitenband (grün) entgegengesetzt.
• Da der blaue und der grüne Zeiger beide mit der gleichen Winkelgeschwindigkeit  $ω_{\rm N}$  drehen, aber in entgegengesetzte Richtungen, ist die vektorielle Summe aller Zeiger stets reell.
• Ist der Modulationsgrad  $m ≤ 1$, so gilt für alle Zeiten  $r_{\rm TP}(t) ≥ 0$  und  $ϕ(t) = 0$. Das bedeutet, dass die Nulldurchgänge des Empfangssignals  $r(t)$  genau mit denen des Trägersignals  $z(t)$  übereinstimmen.
• Die Hüllkurve  $a(t)$  des physikalischen Signals  $r(t)$  ist gleich der resultierenden Zeigerlänge, also gleich dem Betrag von  $r_{\rm TP}(t)$. Wegen  $m< 1$  gilt  $a(t) = q(t) + A_{\rm T}$.
• Bei den gegebenen Amplitudenwerten liegt die Ortskurve  $r_{\rm TP}(t)$  auf der reellen Achse zwischen den Endpunkten  $A_{\rm T} \ – \ A_{\rm N} = 1\ \rm V$  und  $A_{\rm T} + A_{\rm N} = 9 \ \rm V$.
• Die Ortskurve auf der reellen Achse in der rechten Halbebene ist ein Indiz dafür, dass das Nachrichtensignal durch einen Hüllkurvendemodulator verzerrungsfrei extrahiert werden kann.

Hüllkurvendemodulation bei verzerrendem Kanal

$\text{Beispiel 5:}$   Betrachten wir nun die gleichen Grafiken für den verzerrenden Kanal mit

• $α_{\rm U} = 1$   ⇒   das untere Seitenband (USB) wird nicht verändert,
• $α_{\rm T} = 0.8$   ⇒   der Träger wird etwas gedämpft,
• $α_{\rm U} = 0.5$  ⇒   das obere Seitenband (OSB) wird mehr gedämpft.

Diese Grafiken lassen sich wie folgt interpretieren:

• Aufgrund der unterschiedlichen Längen von grünem Zeiger (USB) und blauem Zeiger (OSB) wird die Ortskurve zu einer Ellipse, deren Mittelpunkt durch den (roten) Träger festliegt.
• Der Winkel zwischen dem komplexwertigen  $r_{\rm TP}(t)$  und dem Koordinatenursprung ist nun nicht mehr durchgängig  $ϕ(t) = 0$, sondern schwankt zwischen  $±ϕ_{\rm max}.$
• Die maximale Phase ist gleich dem Winkel der Tangente an die Ellipse. Im physikalischen Signal führt  $ϕ(t) ≠ 0$  zu Verschiebungen der Nulldurchgänge von  $r(t)$  gegenüber seinen Solllagen – vorgegeben durch das Trägersignal  $z(t)$.
• Der Betrag  $a(t) = \vert r_{\rm TP}(t) \vert$ – also die Hüllkurve von  $r(t)$ – ist nun nicht mehr cosinusförmig und das Signal nach dem Hüllkurvendemodulator beinhaltet außer der Frequenz  $f_{\rm N}$  auch Oberwellen:

$$v(t) = A_{\rm 1} \cdot \cos(\omega_{\rm N}\cdot t ) +A_{\rm 2} \cdot \cos(2\omega_{\rm N}\cdot t )+A_{\rm 3} \cdot \cos(3\omega_{\rm N} \cdot t )+ \text{...}$$

• Diese führen zu nichtlinearen Verzerrungen und werden durch den Klirrfaktor  $K$  erfasst.
  Mit  $A_{\rm N} = 4 \ \rm V$,  $A_{\rm T} = 5 \ \rm V$,  $α_{\rm U} = 1$  und  $α_{\rm T} = 0.8$  ergeben sich in Abhängigkeit von  $α_{\rm O}$  folgende Zahlkenwerte:

$α_{\rm O} = 1.00$:     $K = 0$   ⇒   lediglich der Träger wird gedämpft,

$α_{\rm O} = 0.75$:     $K ≈ 0.4\%$,

$α_{\rm O} = 0.50$:     $K ≈ 1.5\%$  ⇒   dieser Wert ist der Grafik zugrunde gelegt,

$α_{\rm O} = 0.25$:     $K ≈ 4\%$,

$α_{\rm O} = 0.00$:     $K ≈ 10\%$   ⇒   vollständige Unterdrückung des OSB.

• Die Grafik gilt für  $α_{\rm O} = 0.5$.  Dann kommt es (allerdings ist beides mit dem bloßen Auge nur schwer zu erkennen)

• zu Verschiebungen der Nulldurchgänge im Signal  $r(t)$  um maximal  $25^\circ\hspace{-0.05cm}/360^\circ ≈ 7\%$ der Trägerperiode $T_0$, und
• zur Abweichung von der idealen Cosinusform   ⇒   $K ≈ 1.5\%$ .

Symmetrische Kanalverzerrungen – Dämpfungsverzerrungen

Ein wesentliches Ergebnis des letzten Abschnitts war, dass es bei unsymmetrischen linearen Verzerrungen auf dem Kanal zu nichtlinearen Verzerrungen bezüglich des Nachrichtensignals kommt.  Wird dagegen das untere Seitenband in gleicher Weise gedämpft wie das obere Seitenband, so ist die Ortskurve wieder eine horizontale Gerade und es entstehen keine nichtlinearen Verzerrungen.  Vielmehr sind dann die Verzerrungen bezüglich  $q(t)$  und  $v(t)$ – ebenso wie die Verzerrungen bezüglich  $s(t)$  und  $r(t)$ – linear und können durch ein geeignet dimensioniertes Filter entzerrt werden.

Wir gehen hier von folgenden Voraussetzungen aus:

• Quellensignal  $q(t)$  – bestehend aus zwei Cosinusanteilen bei den Frequenzen  $f_1$  und  $f_2$  mit den Amplituden  $A_1$  und  $A_2$;
• ZSB–AM mit Träger   ⇒   das Sendesignal  $s(t)$  setzt sich aus insgesamt fünf Cosinusschwingungen bei den Frequenzen  $f_{\rm T},  f_{\rm T} ± f_1$  und  $f_{\rm T} ± f_2$  zusammen;

Spektren im äquivalenten Tiefpass-Bereich

• Kanal mit Dämpfungsverzerrungen, symmetrisch um die Trägerfrequenz:

$$H_{\rm K} (f = f_{\rm T})= \alpha_0, \hspace{0.3cm} H_{\rm K} (f = \pm f_{\rm 1})= \alpha_1, \hspace{0.3cm}H_{\rm K} (f = \pm f_{\rm 2})= \alpha_2;$$

• Idealer Hüllkurvendemodulator gemäß der Beschreibung in diesem Abschnitt.

Die Grafik zeigt die Spektralfunktionen der äquivalenten Tiefpass–Signale von Sende– und Empfangssignal.  Anhand dieses Bildes sind folgende Aussagen möglich:

• Das äquivalente Tiefpass–Signal  $r_{\rm TP}(t)$  ist reell.  Die Ortskurve – also die Spitze des Zeigerverbundes in der komplexen Ebene – liegt auch hier wieder auf der reellen Achse.
• Ist  $α_0 · A_{\rm T}$  größer als  $α_1 · A_1 + α_2 · A_2,$ so ist der „Modulationsgrad des Empfangssignals” kleiner als  $1$  und es kommt nicht zu nichtlinearen Verzerrungen.
• Das Sinkensignal nach idealer Hüllkurvendemodulation und Eliminierung des Gleichanteils  $α_0 · A_{\rm T}$  durch den nachgeschalteten Hochpass lautet:

$$v(t) = \alpha_1 \cdot A_{\rm 1} \cdot \cos(2 \pi f_{\rm 1} t ) + \alpha_2 \cdot A_{\rm 2} \cdot \cos(2 \pi f_{\rm 2} t ) \hspace{0.05cm}.$$

• Das bedeutet:   Es kommt zu linearen Verzerrungen (Dämpfungsverzerrungen), falls  $α_2 ≠ α_1$  ist.  Wäre die Symmetrie bezüglich  $f_{\rm T}$  nicht gegeben, so würden nichtlineare Verzerrungen entstehen.

Wir verweisen auf das Lernvideo  Lineare und nichtlineare Verzerrungen.

Einfluss von Rauschstörungen

Sinkenstörabstand bei "ZSB-AM mit/ohne Träger" und Hüllkurvendemodulation

Ausgehend von der Systemkonfiguration

• ZSB–Amplitudenmodulation mit Modulationsgrad  $m ≤ 1$  sowie
• bestmöglich angepasste Hüllkurvendemodulation

wird nun der Einfluss von additivem Rauschen abgeschätzt.  Verzerrungen jeglicher Art – beispielsweise bedingt durch einen ungeeigneten Kanal oder die nichtperfekte Realisierung von Modulator und Demodulator – werden ausgeschlossen.

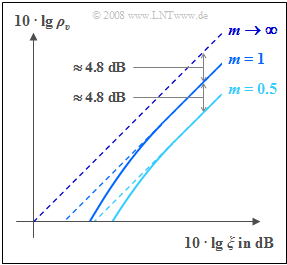
Die Grafik zeigt den Sinkenstörabstand  $10 · \lg \, ρ_v$  bei unterschiedlichem Modulationsgrad  $m$  in Abhängigkeit der logarithmierten Leistungskenngröße

$$10 \cdot {\rm lg }\hspace{0.1cm} \xi = 10 \cdot {\rm lg }\hspace{0.1cm} \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}} \hspace{0.05cm}.$$

Das Ergebnis des Hüllkurvendemodulators ist mit durchgezogenen Linien markiert, während die gestrichelten Geraden den Synchrondemodulator kennzeichnen.

Wie bereits in Kapitel  Untersuchungen im Hinblick auf Signalverzerrungen  hergeleitet wurde, ergeben sich für den Synchrondemodulator in dieser doppelt–logarithmischen Darstellung

• die Winkelhalbierende  (für  $m → ∞$, ZSB–AM ohne Träger), bzw.
• hierzu parallel verschobene Gerade mit vertikalem Abstand  $10 · \lg \, (1 + 2/m^2$).

Bei Anwendung von Hüllkurvendemodulation sind folgende Unterschiede festzustellen:

• Ein Hüllkurvendemodulator ist für  $m > 1$  nicht sinnvoll, da dadurch starke nichtlineare Verzerrungen entstehen würden.
• Die durchgehend gezeichneten Kurven für den Hüllkurvendemodulator  $\rm (HKD)$  liegen stets unterhalb der für den Synchrondemodulator  $\rm (SD)$  gültigen gestrichelten Geraden, wenn man vom gleichen Modulationsgrad  $m$  ausgeht.
• Ab einem gewissen Wert der Leistungskenngröße  $ξ$  sind die  $\rm HKD$–Kurven von den  $\rm SD$–Geraden innerhalb der Zeichengenauigkeit nicht mehr zu unterscheiden.

Mehr Informationen zu dieser Thematik finden Sie beispielsweise in  [Kam 04].

Argumente für und gegen den Hüllkurvendemodulator

Der wichtigste Grund für die Verwendung des Hüllkurvendemodulators ist  (besser gesagt:  war), dass damit die oft aufwändige Frequenz– und Phasensynchronisation vermieden wurde, so dass dieser preisgünstig realisiert werden konnte.  Der Hüllkurvendemodulator ist somit ein Beispiel eines inkohärenten Demodulators.

Für den  Synchrondemodulator  und gegen den Hüllkurvendemodulator können dagegen mehrere Gründe angeführt werden:

• Bei Hüllkurvendemodulation muss eine Übermodulation  $(m > 1)$  unter allen Umständen vermieden werden.  Dies erreicht man beispielsweise durch die Amplitudenbegrenzung des Quellensignals, was aber ebenfalls nichtlineare Verzerrungen zur Folge hat.
• Bei sonst gleichen Randbedingungen ist ein Modulationsgrad  $m < 1$  nur durch die Erhöhung der Sendeleistung um mindestens den Faktor  $3$  zu erreichen.  Dies ist auch wegen der berechtigten Diskussionen zum Thema „Elektro-Smog” in großen Teilen unserer Gesellschaft problematisch.
• Lineare Kanalverzerrungen können bei einem Hüllkurvendemodulator zu irreversiblen nichtlinearen Verzerrungen führen, während die bei Synchrondemodulation entstehenden linearen Verzerrungen möglicherweise durch besondere Maßnahmen beim Empfänger kompensiert werden können.

Aufgaben zum Kapitel

Aufgabe 2.7: Ist der Modulationsgrad zu groß?

Aufgabe 2.7Z: ZSB-AM und Hüllkurvendemodulator

Aufgabe 2.8: Unsymmetrischer Kanal

Aufgabe 2.9: Symmetrische Verzerrungen