Difference between revisions of "Theory of Stochastic Signals/Cross-Correlation Function and Cross Power-Spectral Density"
| Line 5: | Line 5: | ||
|Nächste Seite=Generalization to N-Dimensional Random Variables | |Nächste Seite=Generalization to N-Dimensional Random Variables | ||
}} | }} | ||
| − | ==Definition of the cross correlation function== | + | ==Definition of the cross-correlation function== |
<br> | <br> | ||
In many engineering applications, one is interested in a quantitative measure to describe the statistical relatedness between different processes or between their pattern signals. | In many engineering applications, one is interested in a quantitative measure to describe the statistical relatedness between different processes or between their pattern signals. | ||
| Line 36: | Line 36: | ||
:$$\varphi_{xy}(\tau) = \alpha \cdot \varphi_{x}(\tau- t_{\rm 0}) .$$}} | :$$\varphi_{xy}(\tau) = \alpha \cdot \varphi_{x}(\tau- t_{\rm 0}) .$$}} | ||
| − | == | + | ==Properties of the cross-correlation function== |
<br> | <br> | ||
| − | + | In the following, essential properties of the cross-correlation function are compiled and important differences to the ACF are elaborated. | |
| − | * | + | *The formation of the cross correlation function is ''not commutative''. Rather, there are always two distinct functions, viz. |
:$$\varphi_{xy}(\tau)={\rm E} \big[{x(t)\cdot y(t+\tau)}\big]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}x(t)\cdot y(t+\tau)\,\, \rm d \it t,$$ | :$$\varphi_{xy}(\tau)={\rm E} \big[{x(t)\cdot y(t+\tau)}\big]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}x(t)\cdot y(t+\tau)\,\, \rm d \it t,$$ | ||
:$$\varphi_{yx}(\tau)={\rm E} \big[{y(t)\cdot x(t+\tau)}\big]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}y(t)\cdot x(t+\tau)\,\, \rm d \it t .$$ | :$$\varphi_{yx}(\tau)={\rm E} \big[{y(t)\cdot x(t+\tau)}\big]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}y(t)\cdot x(t+\tau)\,\, \rm d \it t .$$ | ||
| − | * | + | *There is a relationship between the two functions $φ_{yx}(τ) = φ_{xy}(-τ)$. In $\text{example 1}$ of the last section, $φ_{yx}(τ)$ would have its maximum at $τ = -3 \ \rm ms$. |
| − | * | + | *In general, the ''maximum CCF'' does not occur at $τ = 0$ $($exception: $y = α - x)$ and the KKF value $φ_{xy}(τ = 0)$ does not have any special, physically interpretable meaning as in the ACF, where this value reflects the process power. |
| − | * | + | *The magnitude of the KKF is less than or equal to the geometric mean of the two signal powers according to the [https://en.wikipedia.org/wiki/Cauchy%E2%80%93Schwarz_inequality Cauchy-Schwarz inequality] for all $τ$-values: |
| − | :$$\varphi_{xy}( \tau) | + | :$$\varphi_{xy}( \tau) \le \sqrt {\varphi_{x}( \tau = 0) \cdot \varphi_{y}( \tau = 0)}.$$ |
| − | * | + | *In $\text{Example 1}$ on the last page, the equal sign applies: |
| − | :$$\varphi_{xy}( \tau = t_{\rm 0}) | + | :$$\varphi_{xy}( \tau = t_{\rm 0}) = \sqrt {\varphi_{x}( \tau = 0) \cdot \varphi_{y}( \tau = 0)} = \alpha \cdot \varphi_{x}( \tau = {\rm 0}) .$$ |
| − | * | + | *If $x(t)$ and $y(t)$ do not contain a common periodic fraction, the limit of the CCF for $τ → ∞$ gives the product of both means: |
:$$\lim_{\tau \rightarrow \infty} \varphi _{xy} ( \tau ) = m_x \cdot m_y .$$ | :$$\lim_{\tau \rightarrow \infty} \varphi _{xy} ( \tau ) = m_x \cdot m_y .$$ | ||
| − | * | + | *If two signals $x(t)$ and $y(t)$ are ''uncorrelated'', then $φ_{xy}(τ) ≡ 0$, that is, it is $φ_{xy}(τ) = 0$ for all values of $τ$. For example, this assumption is justified in most cases when considering a useful signal and an interfering signal together. |
| − | * | + | *It should always be noted, however, that the CCF includes only the ''linear statistical bindings'' between the signals $x(t)$ and $y(t)$ . Bindings of other types - such as for the case $y(t) = x^2(t)$ - on the other hand, are not taken into account in the CCF formation. |
==Anwendungen der Kreuzkorrelationsfunktion== | ==Anwendungen der Kreuzkorrelationsfunktion== | ||
Revision as of 16:40, 8 March 2022
Contents
Definition of the cross-correlation function
In many engineering applications, one is interested in a quantitative measure to describe the statistical relatedness between different processes or between their pattern signals.
One such measure is the cross-correlation function (CCF), which is given here under the assumptions of stationarity and ergodicity .
$\text{Definition:}$ For the cross-correlation function' of two stationary and ergodic processes with the pattern functions $x(t)$ and $y(t)$ holds:
- $$\varphi_{xy}(\tau)={\rm E} \big[{x(t)\cdot y(t+\tau)}\big]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M} }\cdot\int^{T_{\rm M}/{\rm 2} }_{-T_{\rm M}/{\rm 2} }x(t)\cdot y(t+\tau)\,\rm d \it t.$$
- The first defining equation characterizes the expected value formation (ensemble averaging),
- while the second equation describes the time averaging over a (as large as possible) measurement period $T_{\rm M}$
.
A comparison with the ACF definition shows many similarities. Setting $y(t) = x(t)$, we get $φ_{xy}(τ) = φ_{xx}(τ)$, i.e., the auto-correlation function, for which, however, in our tutorial we mostly use the simplified notation $φ_x(τ)$ .
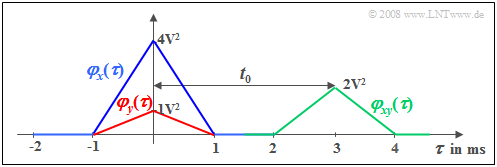
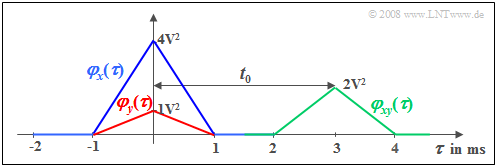
$\text{Example 1:}$ We consider a random signal $x(t)$ with triangular ACF $φ_x(τ)$ ⇒ blue curve. This ACF shape results, for example.
- for a binary signal with equal probability bipolar amplitude coefficients $(+1$ resp. $-1)$ and
- for rectangular fundamental momentum.
We consider a second signal $y(t) = \alpha \cdot x (t - t_{\rm 0}),$ which differs from $x(t)$ only by an attenuation factor $(α =0.5)$ and a transit time $(t_0 = 3 \ \rm ms)$ ;
This attenuated and shifted signal has the ACF drawn in red.
- $$\varphi_{y}(\tau) = \alpha^2 \cdot \varphi_{x}(\tau) .$$
The shift around $t_0$ is not seen in the ACF in contrast to the cross correlation function (CCF) (shown in green) for which the following relation holds:
- $$\varphi_{xy}(\tau) = \alpha \cdot \varphi_{x}(\tau- t_{\rm 0}) .$$
Properties of the cross-correlation function
In the following, essential properties of the cross-correlation function are compiled and important differences to the ACF are elaborated.
- The formation of the cross correlation function is not commutative. Rather, there are always two distinct functions, viz.
- $$\varphi_{xy}(\tau)={\rm E} \big[{x(t)\cdot y(t+\tau)}\big]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}x(t)\cdot y(t+\tau)\,\, \rm d \it t,$$
- $$\varphi_{yx}(\tau)={\rm E} \big[{y(t)\cdot x(t+\tau)}\big]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}y(t)\cdot x(t+\tau)\,\, \rm d \it t .$$
- There is a relationship between the two functions $φ_{yx}(τ) = φ_{xy}(-τ)$. In $\text{example 1}$ of the last section, $φ_{yx}(τ)$ would have its maximum at $τ = -3 \ \rm ms$.
- In general, the maximum CCF does not occur at $τ = 0$ $($exception: $y = α - x)$ and the KKF value $φ_{xy}(τ = 0)$ does not have any special, physically interpretable meaning as in the ACF, where this value reflects the process power.
- The magnitude of the KKF is less than or equal to the geometric mean of the two signal powers according to the Cauchy-Schwarz inequality for all $τ$-values:
- $$\varphi_{xy}( \tau) \le \sqrt {\varphi_{x}( \tau = 0) \cdot \varphi_{y}( \tau = 0)}.$$
- In $\text{Example 1}$ on the last page, the equal sign applies:
- $$\varphi_{xy}( \tau = t_{\rm 0}) = \sqrt {\varphi_{x}( \tau = 0) \cdot \varphi_{y}( \tau = 0)} = \alpha \cdot \varphi_{x}( \tau = {\rm 0}) .$$
- If $x(t)$ and $y(t)$ do not contain a common periodic fraction, the limit of the CCF for $τ → ∞$ gives the product of both means:
- $$\lim_{\tau \rightarrow \infty} \varphi _{xy} ( \tau ) = m_x \cdot m_y .$$
- If two signals $x(t)$ and $y(t)$ are uncorrelated, then $φ_{xy}(τ) ≡ 0$, that is, it is $φ_{xy}(τ) = 0$ for all values of $τ$. For example, this assumption is justified in most cases when considering a useful signal and an interfering signal together.
- It should always be noted, however, that the CCF includes only the linear statistical bindings between the signals $x(t)$ and $y(t)$ . Bindings of other types - such as for the case $y(t) = x^2(t)$ - on the other hand, are not taken into account in the CCF formation.
Anwendungen der Kreuzkorrelationsfunktion
Die Anwendungen der Kreuzkorrelationsfunktion in Nachrichtensystemen sind vielfältig. Hier einige Beispiele:
$\text{Beispiel 2:}$ Bei Amplitudenmodulation, aber auch bei BPSK-Systemen (Binary Phase Shift Keying) wird zur Demodulation (Rücksetzung des Signals in den ursprünglichen Frequenzbereich) sehr häufig der so genannte Synchrondemodulator verwendet, wobei auch beim Empfänger ein Trägersignal zugesetzt werden muss, und zwar frequenz– und phasensynchron zum Sender. Bildet man die KKF zwischen dem Empfangssignal und dem empfangsseitigen Trägersignal, so lässt sich anhand der Spitze der KKF die phasensynchrone Lage zwischen den beiden Signalen erkennen, und es kann bei Auseinanderdriften nachgeregelt werden.
$\text{Beispiel 3:}$ Das Mehrfachzugriffsverfahren CDMA (Code Division Multiple Access) wird zum Beispiel im Mobilfunkstandard UMTS angewendet. Es erfordert eine strenge Phasensynchronität, und zwar bezüglich der zugesetzten Pseudonoise-Folgen beim Sender (Bandspreizung) und beim Empfänger (Bandstauchung). Auch dieses Synchronisationsproblem löst man meist mittels der Kreuzkorrelationsfunktion.
$\text{Beispiel 4:}$ Mit Hilfe der Kreuzkorrelationsfunktion kann festgestellt werden, ob in einem verrauschten Empfangssignal $r(t) = α · s(t – t_0) + n(t)$ ein bekanntes Signal $s(t)$ vorhanden ist oder nicht, und wenn ja, zu welchem Zeitpunkt $t_0$ es auftritt. Aus dem berechneten Wert für $t_0$ lässt sich dann beispielsweise eine Fahrgeschwindigkeit ermitteln (Radartechnik). Diese Aufgabenstellung kann auch mit dem so genannten Matched–Filter gelöst werden, das in einem späteren Kapitel noch beschrieben wird und das viele Gemeinsamkeiten mit der Kreuzkorrelationsfunktion aufweist.
$\text{Beispiel 5:}$ Beim so genannten Korrelationsempfänger verwendet man die KKF zur Signaldetektion. Hierbei bildet man die Kreuzkorrelation zwischen dem durch Rauschen und eventuell auch durch Verzerrungen verfälschten Empfangssignal $r(t)$ und allen möglichen Sendesignalen $s_i(t)$, wobei für den Laufindex $i = 1$, ... , $I$ gelten soll. Entscheidet man $N$ Binärsymbole gemeinsam, so ist $I = {\rm 2}^N$. Man entscheidet sich dann für die Symbolfolge mit dem größten KKF-Wert und erreicht so die minimale Fehlerwahrscheinlichkeit entsprechend der Maximum-Likelihood-Entscheidungsregel.
Kreuzleistungsdichtespektrum
Für manche Anwendungen kann es durchaus vorteilhaft sein, die Korrelation zwischen zwei Zufallssignalen im Frequenzbereich zu beschreiben.
$\text{Definition:}$ Die beiden Kreuzleistungsdichtespektren ${\it Φ}_{xy}(f)$ und ${\it Φ}_{yx}(f)$ ergeben sich aus den dazugehörigen Kreuzkorrelationsfunktionen $\varphi_{xy}({\it \tau})$ bzw. $\varphi_{yx}({\it \tau})$ durch die Fouriertransformation:
- $${\it \Phi}_{xy}(f)=\int^{+\infty}_{-\infty}\varphi_{xy}({\it \tau}) \cdot {\rm e}^{ {\rm -j}\pi f \tau} \rm d \it \tau, $$
- $${\it \Phi}_{yx}(f)=\int^{+\infty}_{-\infty}\varphi_{yx}({\it \tau}) \cdot {\rm e}^{ {\rm -j}\pi f \tau} \rm d \it \tau.$$
Manchmal wird hierfür auch der Begriff spektrale Kreuzleistungsdichte verwendet.
Es gilt hier der gleiche Zusammenhang wie
- zwischen einem deterministischen Signal $x(t)$ und seinem Spektrum $X(f)$ bzw.
- zwischen der Autokorrelationsfunktion ${\it φ}_x(τ)$ eines ergodischen Prozesses $\{x_i(t)\}$ und dem dazugehörigen Leistungsdichtespektrum ${\it Φ}_x(f)$.
Ebenso beschreibt hier die Fourierrücktransformation ⇒ „Zweites Fourierintegral” den Übergang vom Spektralbereich in den Zeitbereich.
$\text{Beispiel 6:}$ Wir nehmen Bezug zum $\text{Beispiel 1}$ mit den beiden „rechteckförmigen Zufallsgrößen” $x(t)$ und $y(t) = α · x(t – t_0)$.
Da die AKF ${\it φ}_x(τ)$ dreieckförmig verläuft, hat – wie im Kapitel Leistungsdichtespektrum beschrieben – das LDS ${\it Φ}_x(f)$ einen ${\rm si}^2$-förmigen Verlauf.
Welche Aussagen können wir allgemein aus dieser Grafik für die Spektralfunktionen ableiten?
- Im zitierten $\text{Beispiel 1}$ haben wir festgestellt, dass sich die Autokorrelationsfunktion ${\it φ}_y(τ)$ von ${\it φ}_x(τ)$ nur um den konstanten Faktor $α^2$ unterscheidet.
- Damit ist klar, dass das Leistungsdichtespektrum ${\it Φ}_y(f)$ von ${\it \Phi}_x(f)$ ebenfalls nur um diesen konstanten Faktor $α^2$ abweicht. Beide Spektralfunktionen sind reell.
- Dagegen besitzt das Kreuzleistungsdichtespektrum einen komplexen Funktionsverlauf:
- $${\it \Phi}_{xy}(f) ={\it \Phi}^\star_{yx}(f)= \alpha \cdot {\it \Phi}_{x}(f) \hspace{0.05cm}\cdot {\rm e}^{- {\rm j } \hspace{0.02cm}\pi f t_0}.$$
Aufgaben zum Kapitel
Aufgabe 4.14: AKF und KKF bei Rechtecksignalen
Aufgabe 4.14Z: Auffinden von Echos