Cross-Correlation Function and Cross Power-Spectral Density

Definition of the cross correlation function

In many engineering applications, one is interested in a quantitative measure to describe the statistical relatedness between different processes or between their pattern signals.

One such measure is the cross-correlation function (CCF), which is given here under the assumptions of stationarity and ergodicity .

$\text{Definition:}$ For the cross-correlation function' of two stationary and ergodic processes with the pattern functions $x(t)$ and $y(t)$ holds:

$$\varphi_{xy}(\tau)={\rm E} \big[{x(t)\cdot y(t+\tau)}\big]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M} }\cdot\int^{T_{\rm M}/{\rm 2} }_{-T_{\rm M}/{\rm 2} }x(t)\cdot y(t+\tau)\,\rm d \it t.$$

The first defining equation characterizes the expected value formation (ensemble averaging),
while the second equation describes the time averaging over a (as large as possible) measurement period $T_{\rm M}$

.

A comparison with the ACF definition shows many similarities. Setting $y(t) = x(t)$, we get $φ_{xy}(τ) = φ_{xx}(τ)$, i.e., the auto-correlation function, for which, however, in our tutorial we mostly use the simplified notation $φ_x(τ)$ .

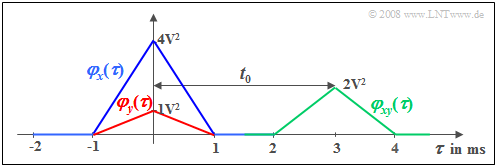
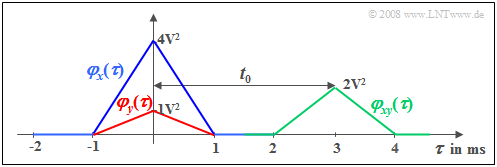
Cross-correlation function of a binary signal

$\text{Example 1:}$ We consider a random signal $x(t)$ with triangular ACF $φ_x(τ)$ ⇒ blue curve. This ACF shape results, for example.

for a binary signal with equal probability bipolar amplitude coefficients $(+1$ resp. $-1)$ and
for rectangular fundamental momentum.

We consider a second signal $y(t) = \alpha \cdot x (t - t_{\rm 0}),$ which differs from $x(t)$ only by an attenuation factor $(α =0.5)$ and a transit time $(t_0 = 3 \ \rm ms)$ ;

This attenuated and shifted signal has the ACF drawn in red.

$$\varphi_{y}(\tau) = \alpha^2 \cdot \varphi_{x}(\tau) .$$

The shift around $t_0$ is not seen in the ACF in contrast to the cross correlation function (CCF) (shown in green) for which the following relation holds:

$$\varphi_{xy}(\tau) = \alpha \cdot \varphi_{x}(\tau- t_{\rm 0}) .$$

Eigenschaften der Kreuzkorrelationsfunktion

Im Folgenden sind wesentliche Eigenschaften der Kreuzkorrelationsfunktion zusammengestellt und es werden wichtige Unterschiede zur AKF herausgearbeitet.

Die Bildung der Kreuzkorrelationsfunktion ist nicht kommutativ. Vielmehr gibt es stets zwei unterschiedliche Funktionen, nämlich

$$\varphi_{xy}(\tau)={\rm E} \big[{x(t)\cdot y(t+\tau)}\big]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}x(t)\cdot y(t+\tau)\,\, \rm d \it t,$$

$$\varphi_{yx}(\tau)={\rm E} \big[{y(t)\cdot x(t+\tau)}\big]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}y(t)\cdot x(t+\tau)\,\, \rm d \it t .$$

Zwischen den beiden Funktionen besteht der Zusammenhang $φ_{yx}(τ) = φ_{xy}(-τ)$. Im $\text{Beispiel 1}$ des letzten Abschnitts hätte $φ_{yx}(τ)$ sein Maximum bei $τ = -3 \ \rm ms$.
Im Allgemeinen tritt das KKF-Maximum nicht bei $τ = 0$ auf $($Ausnahme: $y = α · x)$ und dem KKF-Wert $φ_{xy}(τ = 0)$ kommt keine besondere, physikalisch interpretierbare Bedeutung zu wie bei der AKF, bei der dieser Wert die Prozessleistung wiedergibt.
Der Betrag der KKF ist nach der Cauchy-Schwarzschen Ungleichung für alle $τ$-Werte kleiner oder gleich dem geometrischen Mittel der beiden Signalleistungen:

$$\varphi_{xy}( \tau) \le \sqrt {\varphi_{x}( \tau = 0) \cdot \varphi_{y}( \tau = 0)}.$$

Im $\text{Beispiel 1}$ auf der letzten Seite gilt das Gleichheitszeichen:

$$\varphi_{xy}( \tau = t_{\rm 0}) = \sqrt {\varphi_{x}( \tau = 0) \cdot \varphi_{y}( \tau = 0)} = \alpha \cdot \varphi_{x}( \tau = {\rm 0}) .$$

Beinhalten $x(t)$ und $y(t)$ keinen gemeinsamen periodischen Anteil, so gibt der Grenzwert der KKF für $τ → ∞$ das Produkt beider Mittelwerte an:

$$\lim_{\tau \rightarrow \infty} \varphi _{xy} ( \tau ) = m_x \cdot m_y .$$

Sind zwei Signale $x(t)$ und $y(t)$ unkorreliert, so gilt $φ_{xy}(τ) ≡ 0$, das heißt, es ist $φ_{xy}(τ) = 0$ für alle Werte von $τ$. Diese Annahme ist beispielsweise bei der gemeinsamen Betrachtung eines Nutz- und eines Störsignals in den meisten Fällen gerechtfertigt.
Es ist jedoch stets zu beachten, dass die KKF nur die linearen statistischen Bindungen zwischen den Signalen $x(t)$ und $y(t)$ beinhaltet. Bindungen anderer Art – wie beispielsweise für den Fall $y(t) = x^2(t)$ – werden dagegen bei der KKF–Bildung nicht berücksichtigt.

Anwendungen der Kreuzkorrelationsfunktion

Die Anwendungen der Kreuzkorrelationsfunktion in Nachrichtensystemen sind vielfältig. Hier einige Beispiele:

$\text{Beispiel 2:}$ Bei Amplitudenmodulation, aber auch bei BPSK-Systemen (Binary Phase Shift Keying) wird zur Demodulation (Rücksetzung des Signals in den ursprünglichen Frequenzbereich) sehr häufig der so genannte Synchrondemodulator verwendet, wobei auch beim Empfänger ein Trägersignal zugesetzt werden muss, und zwar frequenz– und phasensynchron zum Sender. Bildet man die KKF zwischen dem Empfangssignal und dem empfangsseitigen Trägersignal, so lässt sich anhand der Spitze der KKF die phasensynchrone Lage zwischen den beiden Signalen erkennen, und es kann bei Auseinanderdriften nachgeregelt werden.

$\text{Beispiel 3:}$ Das Mehrfachzugriffsverfahren CDMA (Code Division Multiple Access) wird zum Beispiel im Mobilfunkstandard UMTS angewendet. Es erfordert eine strenge Phasensynchronität, und zwar bezüglich der zugesetzten Pseudonoise-Folgen beim Sender (Bandspreizung) und beim Empfänger (Bandstauchung). Auch dieses Synchronisationsproblem löst man meist mittels der Kreuzkorrelationsfunktion.

$\text{Beispiel 4:}$ Mit Hilfe der Kreuzkorrelationsfunktion kann festgestellt werden, ob in einem verrauschten Empfangssignal $r(t) = α · s(t – t_0) + n(t)$ ein bekanntes Signal $s(t)$ vorhanden ist oder nicht, und wenn ja, zu welchem Zeitpunkt $t_0$ es auftritt. Aus dem berechneten Wert für $t_0$ lässt sich dann beispielsweise eine Fahrgeschwindigkeit ermitteln (Radartechnik). Diese Aufgabenstellung kann auch mit dem so genannten Matched–Filter gelöst werden, das in einem späteren Kapitel noch beschrieben wird und das viele Gemeinsamkeiten mit der Kreuzkorrelationsfunktion aufweist.

$\text{Beispiel 5:}$ Beim so genannten Korrelationsempfänger verwendet man die KKF zur Signaldetektion. Hierbei bildet man die Kreuzkorrelation zwischen dem durch Rauschen und eventuell auch durch Verzerrungen verfälschten Empfangssignal $r(t)$ und allen möglichen Sendesignalen $s_i(t)$, wobei für den Laufindex $i = 1$, ... , $I$ gelten soll. Entscheidet man $N$ Binärsymbole gemeinsam, so ist $I = {\rm 2}^N$. Man entscheidet sich dann für die Symbolfolge mit dem größten KKF-Wert und erreicht so die minimale Fehlerwahrscheinlichkeit entsprechend der Maximum-Likelihood-Entscheidungsregel.

Kreuzleistungsdichtespektrum

Für manche Anwendungen kann es durchaus vorteilhaft sein, die Korrelation zwischen zwei Zufallssignalen im Frequenzbereich zu beschreiben.

$\text{Definition:}$ Die beiden Kreuzleistungsdichtespektren ${\it Φ}_{xy}(f)$ und ${\it Φ}_{yx}(f)$ ergeben sich aus den dazugehörigen Kreuzkorrelationsfunktionen $\varphi_{xy}({\it \tau})$ bzw. $\varphi_{yx}({\it \tau})$ durch die Fouriertransformation:

$${\it \Phi}_{xy}(f)=\int^{+\infty}_{-\infty}\varphi_{xy}({\it \tau}) \cdot {\rm e}^{ {\rm -j}\pi f \tau} \rm d \it \tau, $$

$${\it \Phi}_{yx}(f)=\int^{+\infty}_{-\infty}\varphi_{yx}({\it \tau}) \cdot {\rm e}^{ {\rm -j}\pi f \tau} \rm d \it \tau.$$

Manchmal wird hierfür auch der Begriff spektrale Kreuzleistungsdichte verwendet.

Es gilt hier der gleiche Zusammenhang wie

zwischen einem deterministischen Signal $x(t)$ und seinem Spektrum $X(f)$ bzw.
zwischen der Autokorrelationsfunktion ${\it φ}_x(τ)$ eines ergodischen Prozesses $\{x_i(t)\}$ und dem dazugehörigen Leistungsdichtespektrum ${\it Φ}_x(f)$.

Ebenso beschreibt hier die Fourierrücktransformation ⇒ „Zweites Fourierintegral” den Übergang vom Spektralbereich in den Zeitbereich.

Zur Definition der Kreuzkorrelationsfunktion

$\text{Beispiel 6:}$ Wir nehmen Bezug zum $\text{Beispiel 1}$ mit den beiden „rechteckförmigen Zufallsgrößen” $x(t)$ und $y(t) = α · x(t – t_0)$.

Da die AKF ${\it φ}_x(τ)$ dreieckförmig verläuft, hat – wie im Kapitel Leistungsdichtespektrum beschrieben – das LDS ${\it Φ}_x(f)$ einen ${\rm si}^2$-förmigen Verlauf.
Welche Aussagen können wir allgemein aus dieser Grafik für die Spektralfunktionen ableiten?

Im zitierten $\text{Beispiel 1}$ haben wir festgestellt, dass sich die Autokorrelationsfunktion ${\it φ}_y(τ)$ von ${\it φ}_x(τ)$ nur um den konstanten Faktor $α^2$ unterscheidet.
Damit ist klar, dass das Leistungsdichtespektrum ${\it Φ}_y(f)$ von ${\it \Phi}_x(f)$ ebenfalls nur um diesen konstanten Faktor $α^2$ abweicht. Beide Spektralfunktionen sind reell.
Dagegen besitzt das Kreuzleistungsdichtespektrum einen komplexen Funktionsverlauf:

$${\it \Phi}_{xy}(f) ={\it \Phi}^\star_{yx}(f)= \alpha \cdot {\it \Phi}_{x}(f) \hspace{0.05cm}\cdot {\rm e}^{- {\rm j } \hspace{0.02cm}\pi f t_0}.$$

Aufgaben zum Kapitel

Aufgabe 4.14: AKF und KKF bei Rechtecksignalen

Aufgabe 4.14Z: Auffinden von Echos