Difference between revisions of "Theory of Stochastic Signals/Wiener–Kolmogorow Filter"
| Line 1: | Line 1: | ||
{{LastPage}} | {{LastPage}} | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Filtering of Stochastic Signals |
|Vorherige Seite=Matched-Filter | |Vorherige Seite=Matched-Filter | ||
|Nächste Seite= | |Nächste Seite= | ||
}} | }} | ||
| − | == | + | ==Optimization criterion of the Wiener-Kolmogorow filter== |
<br> | <br> | ||
| − | + | As another example of optimal filtering, we now consider the task of reconstructing as well as possible the shape of an useful signal $s(t)$ from the reception signal $r(t)$, which is disturbed by additive noise $n(t)$, in terms of the ''mean square error'' (MSE): | |
:$${\rm{MQF}} = \mathop {\lim }\limits_{T_{\rm M} \to \infty } \frac{1}{{T_{\rm M} }}\int_{ - T_{\rm M} /2}^{+T_{\rm M} /2} {\left| {d(t) - s(t)} \right|^2 \, {\rm{d}}t} \mathop = \limits^! {\rm{Minimum}}.$$ | :$${\rm{MQF}} = \mathop {\lim }\limits_{T_{\rm M} \to \infty } \frac{1}{{T_{\rm M} }}\int_{ - T_{\rm M} /2}^{+T_{\rm M} /2} {\left| {d(t) - s(t)} \right|^2 \, {\rm{d}}t} \mathop = \limits^! {\rm{Minimum}}.$$ | ||
| − | + | The filter is named after its inventors [https://en.wikipedia.org/wiki/Norbert_Wiener Norbert Wiener] and [https://en.wikipedia.org/wiki/Andrey_Kolmogorov Andrei Nikolajewitsch Kolmogorow]. We denote the corresponding frequency response by $H_{\rm WF}(f).$ | |
| − | [[File:EN_Sto_T_5_5_S1.png|right |frame| | + | [[File:EN_Sto_T_5_5_S1.png|right |frame| Derivation of the Wiener filter]] |
| − | + | The following conditions apply to this optimization task: | |
| − | * | + | *The signal $s(t)$ to be reconstructed is the result of a random process $\{s(t)\}$, of which only the statistical properties are known in the form of the power-spectral density ${\it Φ}_s(f)$. |
| − | * | + | *The interference signal $n(t)$ is given by the PSD ${\it Φ}_n(f)$. Correlations between the useful and interference signals are accounted for by the [[Theory_of_Stochastic_Signals/Kreuzkorrelationsfunktion_und_Kreuzleistungsdichte#Kreuzleistungsdichtespektrum|cross-power density spectra]] ${\it Φ}_{sn}(f) = \hspace{0.1cm} –{ {\it Φ}_{ns} }^∗(f)$. |
| − | * | + | *The output signal of the sought filter is denoted by $d(t)$, which should differ as little as possible from $s(t)$ according to the MSE. $T_{\rm M}$ again denotes the measurement duration. |
<br clear=all> | <br clear=all> | ||
| − | + | Let the signal $s(t)$ be mean-free $(m_s = 0)$ and power-limited. This means: The signal energy $E_s$ is infinite due to the infinite extension of the signal $s(t)$ and the signal power has a finite value: | |
:$$P_s = \mathop {\lim }\limits_{T_{\rm M} \to \infty } \frac{1}{{T_{\rm M} }}\int_{ - T_{\rm M} /2}^{+T_{\rm M} /2} |{s(t)|^2 \, {\rm{d}}t > 0.}$$ | :$$P_s = \mathop {\lim }\limits_{T_{\rm M} \to \infty } \frac{1}{{T_{\rm M} }}\int_{ - T_{\rm M} /2}^{+T_{\rm M} /2} |{s(t)|^2 \, {\rm{d}}t > 0.}$$ | ||
| − | * | + | *A fundamental difference with the matched filter task is the stochastic and power-limited useful signal $s(t)$. |
| − | * | + | *Let us recall: In the matched filter, the signal $g(t)$ to be reconstructed was deterministic, limited in time and thus also energy-limited. |
| − | == | + | ==Result of the filter optimization== |
<br> | <br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Here without proof:}$ The '''transmission function of the optimal filter''' can be determined by the so-called ''Wiener-Hopf integral equation'', and is: |
:$$H_{\rm WF} (f) = \frac{{ {\it \Phi }_s (f) + {\it \Phi }_{ns} (f)} }{ { {\it \Phi }_s (f) + {\it \Phi }_{sn} (f) + {\it \Phi }_{ns} (f) + {\it \Phi }_n (f)}}.$$ | :$$H_{\rm WF} (f) = \frac{{ {\it \Phi }_s (f) + {\it \Phi }_{ns} (f)} }{ { {\it \Phi }_s (f) + {\it \Phi }_{sn} (f) + {\it \Phi }_{ns} (f) + {\it \Phi }_n (f)}}.$$ | ||
| − | *[https:// | + | *[https://en.wikipedia.org/wiki/Andrey_Kolmogorov A. Kolmogorow] and [https://en.wikipedia.org/wiki/Norbert_Wiener N. Wiener] independently solved this optimization problem almost at the same time. |
| − | * | + | *The index "WF" stands for Wiener filter and unfortunately does not reveal the merits of Kolmogorov. |
| − | * | + | *The derivation of this result is not trivial and can be found for example in [Hän97]<ref>Hänsler, E.: ''Statistische Signale: Grundlagen und Anwendungen.'' 2. Auflage. Berlin – Heidelberg: Springer, 1997.</ref>. }} |
| − | + | The mathematical derivation of the equation is omitted. Rather, this filter shall be clarified and interpreted in the following on the basis of some special cases. | |
| − | * | + | *If signal and disturbance are uncorrelated ⇒ ${\it Φ}_{sn}(f) = {\it Φ}_{ns}(f) = 0$, the above equation simplifies as follows: |
:$$H_{\rm WF} (f) = \frac{{ {\it \Phi }_s (f) }}{{ {\it \Phi }_s (f) + {\it \Phi }_n (f) }} = \frac{1}{{1 + {\it \Phi }_n (f) / {\it \Phi }_s (f) }}.$$ | :$$H_{\rm WF} (f) = \frac{{ {\it \Phi }_s (f) }}{{ {\it \Phi }_s (f) + {\it \Phi }_n (f) }} = \frac{1}{{1 + {\it \Phi }_n (f) / {\it \Phi }_s (f) }}.$$ | ||
| − | * | + | *The filter then acts as a frequency-dependent divider, with the divider ratio determined by the power-spectral densities of the useful signal and the interference signal. |
| − | * | + | *The "passband" is predominantly at the frequencies where the useful signal has much larger components than the interference: |
:$${\it Φ}_s(f) \gg {\it Φ}_n(f).$$ | :$${\it Φ}_s(f) \gg {\it Φ}_n(f).$$ | ||
| − | * | + | *The ''mean square error'' (MSE) between the filter output signal $d(t)$ and the input signal $s(t)$ is |
:$${\rm MQF} = \int\limits_{ - \infty }^{ + \infty } {\frac{{ {\it \Phi }_s (f) \cdot {\it \Phi }_n (f)}}{{ {\it \Phi }_s(f) + {\it \Phi }_n (f)}}\,{\rm{d}}f = \int\limits_{ - \infty }^{ + \infty } {H_{\rm WF} (f) \cdot {\it \Phi }_n (f)}\, {\rm{d}}f.}$$ | :$${\rm MQF} = \int\limits_{ - \infty }^{ + \infty } {\frac{{ {\it \Phi }_s (f) \cdot {\it \Phi }_n (f)}}{{ {\it \Phi }_s(f) + {\it \Phi }_n (f)}}\,{\rm{d}}f = \int\limits_{ - \infty }^{ + \infty } {H_{\rm WF} (f) \cdot {\it \Phi }_n (f)}\, {\rm{d}}f.}$$ | ||
| − | ==Interpretation | + | ==Interpretation of the Wiener filter== |
<br> | <br> | ||
| − | + | Now we will illustrate the Wiener-Kolmogorov filter with two examples. | |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 1:}$ To illustrate the Wiener filter, we consider as a limiting case a transmission signal $s(t)$ with the power-spectral density ${\it Φ}_s(f) = P_{\rm S} · δ(f ± f_{\rm S}).$ |
| − | * | + | *Thus, it is known that $s(t)$ is a harmonic oscillation with frequency $f_{\rm S}$. |
| − | * | + | *On the other hand, the amplitude and phase of the current sample function $s(t)$ are unknown. |
| − | + | With white noise ⇒ ${\it Φ}_n(f) = N_0/2$ the frequency response of the Wiener filter is thus: | |
:$$H_{\rm WF} (f) = \frac{1}{ {1 +({N_0 /2})/{\big[ P_{\rm S} \cdot\delta ( {f \pm f_{\rm S} } \big ]} })}.$$ | :$$H_{\rm WF} (f) = \frac{1}{ {1 +({N_0 /2})/{\big[ P_{\rm S} \cdot\delta ( {f \pm f_{\rm S} } \big ]} })}.$$ | ||
*Bei allen Frequenzen mit Ausnahme von $f = ±f_{\rm S}$ ergibt sich $H_{\rm WF}(f) = 0$, da hier der Nenner unendlich groß wird. | *Bei allen Frequenzen mit Ausnahme von $f = ±f_{\rm S}$ ergibt sich $H_{\rm WF}(f) = 0$, da hier der Nenner unendlich groß wird. | ||
Revision as of 16:58, 26 January 2022
Contents
Optimization criterion of the Wiener-Kolmogorow filter
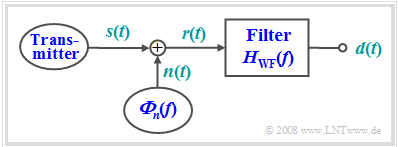
As another example of optimal filtering, we now consider the task of reconstructing as well as possible the shape of an useful signal $s(t)$ from the reception signal $r(t)$, which is disturbed by additive noise $n(t)$, in terms of the mean square error (MSE):
- $${\rm{MQF}} = \mathop {\lim }\limits_{T_{\rm M} \to \infty } \frac{1}{{T_{\rm M} }}\int_{ - T_{\rm M} /2}^{+T_{\rm M} /2} {\left| {d(t) - s(t)} \right|^2 \, {\rm{d}}t} \mathop = \limits^! {\rm{Minimum}}.$$
The filter is named after its inventors Norbert Wiener and Andrei Nikolajewitsch Kolmogorow. We denote the corresponding frequency response by $H_{\rm WF}(f).$
The following conditions apply to this optimization task:
- The signal $s(t)$ to be reconstructed is the result of a random process $\{s(t)\}$, of which only the statistical properties are known in the form of the power-spectral density ${\it Φ}_s(f)$.
- The interference signal $n(t)$ is given by the PSD ${\it Φ}_n(f)$. Correlations between the useful and interference signals are accounted for by the cross-power density spectra ${\it Φ}_{sn}(f) = \hspace{0.1cm} –{ {\it Φ}_{ns} }^∗(f)$.
- The output signal of the sought filter is denoted by $d(t)$, which should differ as little as possible from $s(t)$ according to the MSE. $T_{\rm M}$ again denotes the measurement duration.
Let the signal $s(t)$ be mean-free $(m_s = 0)$ and power-limited. This means: The signal energy $E_s$ is infinite due to the infinite extension of the signal $s(t)$ and the signal power has a finite value:
- $$P_s = \mathop {\lim }\limits_{T_{\rm M} \to \infty } \frac{1}{{T_{\rm M} }}\int_{ - T_{\rm M} /2}^{+T_{\rm M} /2} |{s(t)|^2 \, {\rm{d}}t > 0.}$$
- A fundamental difference with the matched filter task is the stochastic and power-limited useful signal $s(t)$.
- Let us recall: In the matched filter, the signal $g(t)$ to be reconstructed was deterministic, limited in time and thus also energy-limited.
Result of the filter optimization
$\text{Here without proof:}$ The transmission function of the optimal filter can be determined by the so-called Wiener-Hopf integral equation, and is:
- $$H_{\rm WF} (f) = \frac{{ {\it \Phi }_s (f) + {\it \Phi }_{ns} (f)} }{ { {\it \Phi }_s (f) + {\it \Phi }_{sn} (f) + {\it \Phi }_{ns} (f) + {\it \Phi }_n (f)}}.$$
- A. Kolmogorow and N. Wiener independently solved this optimization problem almost at the same time.
- The index "WF" stands for Wiener filter and unfortunately does not reveal the merits of Kolmogorov.
- The derivation of this result is not trivial and can be found for example in [Hän97][1].
The mathematical derivation of the equation is omitted. Rather, this filter shall be clarified and interpreted in the following on the basis of some special cases.
- If signal and disturbance are uncorrelated ⇒ ${\it Φ}_{sn}(f) = {\it Φ}_{ns}(f) = 0$, the above equation simplifies as follows:
- $$H_{\rm WF} (f) = \frac{{ {\it \Phi }_s (f) }}{{ {\it \Phi }_s (f) + {\it \Phi }_n (f) }} = \frac{1}{{1 + {\it \Phi }_n (f) / {\it \Phi }_s (f) }}.$$
- The filter then acts as a frequency-dependent divider, with the divider ratio determined by the power-spectral densities of the useful signal and the interference signal.
- The "passband" is predominantly at the frequencies where the useful signal has much larger components than the interference:
- $${\it Φ}_s(f) \gg {\it Φ}_n(f).$$
- The mean square error (MSE) between the filter output signal $d(t)$ and the input signal $s(t)$ is
- $${\rm MQF} = \int\limits_{ - \infty }^{ + \infty } {\frac{{ {\it \Phi }_s (f) \cdot {\it \Phi }_n (f)}}{{ {\it \Phi }_s(f) + {\it \Phi }_n (f)}}\,{\rm{d}}f = \int\limits_{ - \infty }^{ + \infty } {H_{\rm WF} (f) \cdot {\it \Phi }_n (f)}\, {\rm{d}}f.}$$
Interpretation of the Wiener filter
Now we will illustrate the Wiener-Kolmogorov filter with two examples.
$\text{Example 1:}$ To illustrate the Wiener filter, we consider as a limiting case a transmission signal $s(t)$ with the power-spectral density ${\it Φ}_s(f) = P_{\rm S} · δ(f ± f_{\rm S}).$
- Thus, it is known that $s(t)$ is a harmonic oscillation with frequency $f_{\rm S}$.
- On the other hand, the amplitude and phase of the current sample function $s(t)$ are unknown.
With white noise ⇒ ${\it Φ}_n(f) = N_0/2$ the frequency response of the Wiener filter is thus:
- $$H_{\rm WF} (f) = \frac{1}{ {1 +({N_0 /2})/{\big[ P_{\rm S} \cdot\delta ( {f \pm f_{\rm S} } \big ]} })}.$$
- Bei allen Frequenzen mit Ausnahme von $f = ±f_{\rm S}$ ergibt sich $H_{\rm WF}(f) = 0$, da hier der Nenner unendlich groß wird.
- Berücksichtigt man weiter, dass $δ(f = ±f_{\rm S})$ an der Stelle $f = ±f_{\rm S}$ unendlich groß ist, so erhält man weiter $H_{\rm MF}(f = ±f_{\rm S} ) = 1. $
- Das optimale Filter ist somit ein Bandpass um $f_{\rm S}$ mit unendlich kleiner Bandbreite.
- Der mittlere quadratische Fehler zwischen dem Sendesignal $s(t)$ und dem Filterausgangssignal $d(t)$ beträgt
- $${\rm{MQF} } = \int_{ - \infty }^{ + \infty } {H_{\rm WF} (f) \cdot {\it \Phi_n} (f) \,{\rm{d} }f = \mathop {\lim }\limits_{\varepsilon \hspace{0.03cm} {\rm > \hspace{0.03cm}0,}\;\;\varepsilon \hspace{0.03cm} \to \hspace{0.03cm}\rm 0 } }\hspace{0.1cm} \int_{f_{\rm S} - \varepsilon }^{f_{\rm S} + \varepsilon }\hspace{-0.3cm} {N_0 }\,\,{\rm{d} }f = 0.$$
- Dieses unendlich schmale Bandpass–Filter würde bei den getroffenen Voraussetzungen die vollständige Regenerierung der Harmonischen hinsichtlich Amplitude und Phase erlauben. Unabhängig von der Größe der Störung $(N_0)$ würde somit $d(t) = s(t)$ gelten.
- Allerdings ist ein unendlich schmales Filter nicht realisierbar. Bei endlicher Bandbreite $Δf$ ist der mittlere quadratische Fehler ${\rm MQF} = N_0 · Δf$.
Dieses Beispiel hat einen Sonderfall behandelt, bei dem das bestmögliche Ergebnis $\rm MQF = 0$ zumindest theoretisch möglich wäre. Das folgende Beispiel geht von realistischeren Annahmen aus und liefert das Ergebnis $\rm MQF > 0$.
$\text{Beispiel 2:}$ Nun betrachten wir ein stochastisches rechteckförmiges Binärsignal $s(t)$, das durch weißes Rauschen $n(t)$ additiv überlagert ist.
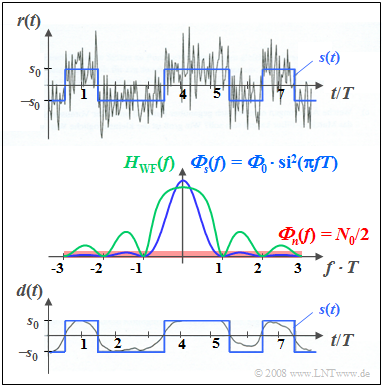
Die Grafik enthält folgende Diagramme:
- Oben ist grau das Summensignal $r(t) = s(t) + n(t)$ für ${\it Φ}_0/N_0 = 5$ dargestellt, wobei ${\it Φ}_0$ die Energie eines Einzelimpulses bezeichnet und $N_0$ die Leistungsdichte des weißen Rauschens angibt. Das Nutzsignal $s(t)$ ist blau gezeichnet.
- In Bildmitte sind die Leistungsdichtespektren ${\it Φ}_s(f)$ und ${\it Φ}_n(f)$ in blauer bzw. roter Farbe skizziert und formelmäßig angegeben. Grün gezeichnet ist der resultierende Frequenzgang $H_{\rm WF}(f)$.
- Das untere Bild zeigt als grauen Kurvenzug das Ausgangssignal $d(t)$ des Wiener-Filters im Vergleich zum blau gezeichneten Sendesignal $s(t)$. Im Idealfall sollte $d(t) = s(t)$ gelten.
Die untere Darstellung zeigt:
(1) Der mittlere quadratische Fehler (MQF) ergibt sich aus dem Vergleich der Signale $d(t)$ und $s(t)$.
(2) Die numerische Auswertung ergab für $\rm MQF$ etwa $11\%$ der Nutzleistung $P_{\rm S} $.
(3) Im Signal $d(t)$ fehlen vorwiegend die höherfrequenten Signalanteile (also die Sprünge).
(4) Diese Anteile werden zugunsten einer besseren Störunterdrückung dieser Frequenzen ausgefiltert.
Mit keinem anderen Filter ergibt sich bei diesen Voraussetzungen ein kleinerer (mittlerer quadratischer) Fehler als mit dem Wiener-Filter.
Dessen Frequenzgang (grüner Kurvenverlauf) lautet hier:
- $$H_{\rm WF} (f) = \frac{1}{ {1 + ({N_0 /2})/( {\it \Phi}_0 \cdot {\rm si^2} ( \pi f T )})} \hspace{0.15cm} .$$
Aus dem mittleren Diagramm erkennt man weiter:
- Der Gleichsignalübertragungsfaktor ergibt sich hier zu $H_{\rm WF}(f = 0) = {\it Φ}_0/({\it Φ}_0 + N_0/2) = 10/11.$
- Bei Vielfachen der Symbolfolgefrequenz $1/T$, bei denen das stochastische Nutzsignal $s(t)$ keine Spektralanteile besitzt, ist $H_{\rm WF}(f) = 0$.
- Je mehr Nutzsignalanteile bei einer bestimmten Frequenz vorhanden sind, desto durchlässiger ist bei dieser Frequenz auch das Wiener-Filter.
Aufgabe zum Kapitel
Aufgabe 5.9: Minimierung des MQF
Quellenverzeichnis
- ↑ Hänsler, E.: Statistische Signale: Grundlagen und Anwendungen. 2. Auflage. Berlin – Heidelberg: Springer, 1997.