Matched Filter Properties
Open Applet in new Tab Deutsche Version Öffnen
Contents
Applet Description
The applet is intended to illustrate the properties of the »matched filter« $({\rm MF})$.
- This is used to optimally detection of amplitude and/or location of a known waveform in a highly noisy environment.
- Or more generally speaking: The matched filter – sometimes also referred to as »optimal filter« or as »correlation filter« – is used to detect the existence of such a signal.
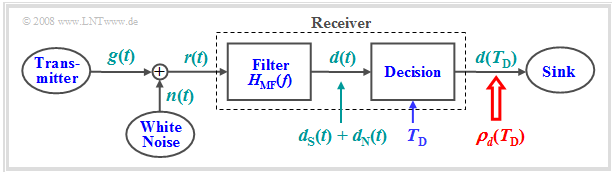
The graphic shows the so-called »matched filter receiver«:
- This can decide with the greatest possible certainty – in other words: with the maximum signal–to–noise–ratio $($ $\rm SNR)$ – whether a pulse-shaped signal component $g(t)$ disturbed by additive noise $n(t)$ is present or not.
- One application is radar technology, where the pulse shape $g(t)$ is known, but not when the pulse was sent and with what strength and delay it arrives.
- However, the matched filter is also used as a receiver filter in digital transmission systems $($or at least as part of them$)$ to minimize the error probability of the system.
All parameters, times and frequencies are to be understood as normalized quantities and thus dimensionless.
- For the »input pulse« $g(t)$, "rectangular", "Gaussian" and "exponential" can be set, each described by the pulse amplitude $A_g$, the equivalent pulse duration $\Delta t_g$ and the shift $\tau_g$ with respect to the time–symmetrical case. Further information in the section »Further information about the considered input pulses«.
- For the »receiver filter« you can choose between the alternatives "slit low-pass" $($rectangular-in-time$)$, "Gaussian low-pass", "first order lowpass" and "extremely acausal filter". The respective impulse responses $h(t)$, are shown, characterized by their height $A_h$, the equivalent duration $\Delta t_h$ and the shift $\tau_h$. More information in the section »Further information on the considered impulse responses«.
- Further input parameters are the detection time $T_{\rm D}$ and the also normalized noise power density $N_0$ at the receiver input.
The following are output as numerical values
- The energy $E_g$ of the input pulse $g(t)$, useful signal value $d_{\rm S} (T_{\rm D})$ at the filter output as well as the noise variance $\sigma_d^2$ at the filter output,
- the signal–to–noise ratio $\rho_{d} (T_{\rm D})$ at the filter output and the corresponding dB specification $10 \cdot \lg \ \rho_{d} (T_{\rm D})$,
- the maximum value for this is $10 \cdot \lg \ \rho_{\rm MF}$.
If the input configuration meets the matched filter conditions, then: $10 \cdot \lg \ \rho_{d} (T_{\rm D,\ opt}) = 10 \cdot \lg \ \rho_{\rm MF}$.
Theoretical Background
Detailed description of the underlying model
The following conditions apply to the individual components:
- Let the useful component $g(t)$ of the received signal $r(t)=g(t)+n(t)$ be pulse-shaped and thus "energy-limited".
- That means: The integral over $\big [g(t)\big ]^2$ from $–∞$ to $+∞$ yields the finite value $E_g$.
- Let the noise signal $n(t)$ be "white Gaussian noise" with (one–sided) noise power density $N_0$.
- The signal $d(t)$ is additively composed of two components: The component $d_{\rm S}(t)$ is due to the "$\rm S$"ignal $g(t)$, the component $d_{\rm N}(t)$ is due to the "$\rm N$"oise $n(t)$.
- The receiver, consisting of a linear filter ⇒ frequency response $H_{\rm MF}(f)$ and the "decision maker", is to be dimensioned
so that the instantaneous S/N ratio at the output is maximized:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {d_{\rm S} ^2 ( {T_{\rm D} } )} }{ {\sigma _d ^2 } }\mathop = \limits^{\rm{!} }\hspace{0.1cm} {\rm{Maximum} }.$$
- Here, $σ_d^2$ denotes the variance ("power") of the signal $d_{\rm N}(t)$, and $T_{\rm D}$ denotes the (suitably chosen) "detection time".
Matched filter optimization
Let be given an energy-limited useful signal $g(t)$ with the corresponding spectrum $G(f)$.
- Thus, the filter output signal at detection time $T_{\rm D}$ for any filter with impulse response $h(t)$ and frequency response $H(f) =\mathcal{ F}\{h(t)\}$ can be written as follows
(ignoring noise ⇒ subscript $\rm S$ for "signal"):
- $$d_{\rm S} ( {T_{\rm D} } ) = g(t) * h(t) = \int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e}}^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }\hspace{0.1cm} {\rm{d}}f} .$$
- The "noise component" $d_{\rm N}(t)$ of the filter output signal (subscript $\rm N$ for "noise") stems solely from the white noise $n(t)$ at the input of the receiver. For its variance (power) applies independently of the detection time $T_{\rm D}$:
- $$\sigma _d ^2 = \frac{ {N_0 } }{2} \cdot \int_{ - \infty }^{ + \infty } {\left| {H(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} .$$
- Thus, the optimization problem at hand is:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {\left| {\int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e} }^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }\hspace{0.1cm} {\rm{d} }f} } \right|^2 } }{ {N_0 /2 \cdot \int_{ - \infty }^{ + \infty } {\left| {H(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } } \stackrel{!}{=} {\rm{Maximum} }.$$
$\text{Here first without proof:}$ One can show that this quotient becomes largest for the following frequency response $H(f)$:
- $$H(f) = H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm e}^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } . $$
- Thus, for the signal–to–noise power ratio at the matched filter output $($independent of the dimensionally constant $K_{\rm MF})$, we obtain:
- $$\rho _d ( {T_{\rm D} } ) = { {2 \cdot E_g } }/{ {N_0 } }.$$
- $E_g$ denotes the energy of the input pulse, which can be calculated using Parseval's theorem in both the time and frequency domains:
- $$E_g = \int_{ - \infty }^{ + \infty } {g^2 (t)\hspace{0.1cm}{\rm{d} }t} = \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right\vert ^{\rm{2} }\hspace{0.1cm} {\rm d}f} .$$
$\text{Example 1:}$ A rectangular pulse $g(t)$ with amplitude $\rm 1\hspace{0.05cm}V$, duration $0.5\hspace{0.05cm} \rm ms$ and unknown position is to be found in a noisy environment.
- Thus the pulse energy $E_g = \rm 5 · 10^{–4} \hspace{0.05cm}V^2s$.
- Let the noise power density be $N_0 = \rm 10^{–6} \hspace{0.05cm}V^2/Hz$.
The best result ⇒ the maximum S/N ratio is obtained with the matched filter:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {2 \cdot E_g } }{ {N_0 } } = \frac{ {2 \cdot 5 \cdot 10^{-4}\, {\rm V^2\,s} } }{ {10^{-6}\, {\rm V^2/Hz} } } = 1000 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.15cm}\rho _d ( {T_{\rm D} } ) = 30\,{\rm dB}.$$
The matched filter criterion given above is now derived step by step. If you are not interested in this, please skip to the next section "Interpretation of the matched filter".
$\text{Derivation of the matched filter criterion:}$
$(1)$ The Schwarz inequality with the two (generally complex) functions $A(f)$ and $B(f)$:
- $$\left \vert {\int_a^b {A(f) \cdot B(f)\hspace{0.1cm}{\rm{d} }f} } \right \vert ^2 \le \int_a^b {\left \vert {A(f)} \right \vert^{\rm{2} } \hspace{0.1cm}{\rm{d} }f} \cdot \int_a^b {\left\vert {B(f)} \right \vert^{\rm{2} } \hspace{0.1cm}{\rm{d} }f} .$$
$(2)$ We now apply this equation to the signal–to–noise ratio:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {\left \vert {\int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e} }^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } \hspace{0.1cm}{\rm{d} }f} } \right \vert^2 } }{ {N_0 /2 \cdot \int_{ - \infty }^{ + \infty } {\left \vert {H(f)} \right \vert^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } }.$$
$(3)$ Thus, with $A(f) = G(f)$ and $B(f) = H(f) · {\rm e}^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }$ the following bound is obtained:
- $$\rho_d ( {T_{\rm D} } ) \le \frac{1}{ {N_0 /2} } \cdot \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert^{\rm{2} } }\hspace{0.1cm}{\rm{d} }f .$$
$(4)$ We now tentatively set for the filter frequency response:
- $$H(f) = H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm{e} }^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }.$$
$(5)$ Then, from the above equation $(2)$, we obtain the following result:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {\left \vert K_{\rm MF}\cdot {\int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert ^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } \right \vert ^2 } }{ {N_0 /2 \cdot K_{\rm MF} ^2 \cdot \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert ^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } } = \frac{1}{ {N_0 /2} } \cdot \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert ^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} .$$
$\text{This means:}$
- With the approach $(4)$ for the matched filter $H_{\rm MF}(f)$, the maximum possible value is indeed obtained in the above estimation.
- No other filter $H(f) ≠ H_{\rm MF}(f)$ can achieve a higher signal–to–noise power ratio.
- The matched filter is optimal with respect to the maximization criterion on which it is based.
Interpretation of the matched filter
In the last section, the frequency response of the matched filter was derived as follows:
- $$H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm{e} }^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } .$$
By Fourier inverse transformation the corresponding impulse response is obtained:
- $$h_{\rm MF} (t) = K_{\rm MF} \cdot g(T_{\rm D} - t).$$
These two functions can be interpreted as follows:
- The "matched filter" is matched by the term $G^{\star}(f)$ to the spectrum of the pulse $g(t)$ which is to be found – hence its name.
- The "constant" $K_{\rm MF}$ is necessary for dimensional reasons.
- If $g(t)$ is a voltage pulse, this constant has the unit "Hz/V". The frequency response $H_{\rm MF} (f)$ is therefore dimensionless.
- The "impulse response" $h_{\rm MF}(t)$ results from the useful signal $g(t)$ by mirroring ⇒ from $g(t)$ becomes $g(–t)$ $]$ as well as a shift by $T_{\rm D}$ to the right.
- The "earliest detection time" $T_{\rm D}$ follows for realizable systems from the condition $h_{\rm MF}(t < 0)\equiv 0$ $($"causality", see book Linear and Time-Invariant Systems$)$.
- The "useful component" $d_{\rm S} (t)$ of the filter output signal is equal in shape to the energy auto-correlation function $\varphi^{^{\bullet} }_{g} (t )$ and shifted with respect to it by $T_{\rm D}$. It holds:
- $$d_{\rm S} (t) = g(t) * h_{\rm MF} (t) = K_{\rm MF} \cdot g(t) * g(T_{\rm D} - t) = K_{\rm MF} \cdot \varphi^{^{\bullet} }_{g} (t - T_{\rm D} ).$$
$\text{Please note:}$ For an energy-limited signal $g(t)$, one can only specify the energy ACF:
- $$\varphi^{^{\bullet} }_g (\tau ) = \int_{ - \infty }^{ + \infty } {g(t) \cdot g(t + \tau )\,{\rm{d} }t} .$$
Compared to the ACF definition of a power-limited signal $x(t)$, viz.
- $$\varphi _x (\tau ) = \mathop {\lim }_{T_{\rm M} \to \infty } \frac{1}{ {T_{\rm M} } }\int_{ - T_{\rm M} /2}^{+T_{\rm M} /2} {x(t) \cdot x(t + \tau )\hspace{0.1cm}\,{\rm{d} }t} ,$$
the division by the measurement duration $T_{\rm M}$ and the boundary transition $T_{\rm M} → ∞$ are omitted in the calculation of the energy ACF.
$\text{Example 2:}$ We assume that the rectangular pulse is between $\rm 2\hspace{0.08cm}ms$ and $\rm 2.5\hspace{0.08cm}ms$ and the detection time $T_{\rm D} =\rm 2\hspace{0.08cm}ms$ is desired.
Under these conditions:
- The matched filter impulse response $h_{\rm MF}(t)$ must be constant in the range from $t_1 (= 4 - 2.5) =\rm 1.5\hspace{0.08cm}ms$ to $t_2 (= 4 - 2) =\rm 2\hspace{0.08cm}ms$.
- For $t < t_1$ as well as for $t > t_2$ it must not have any components.
- The magnitude frequency response $\vert H_{\rm MF}(f)\vert$ is $\rm sinc$–shaped here.
- The magnitude of the impulse response $h_{\rm MF}(t)$ is not important for the S/N ratio, because $\rho _d ( {T_{\rm D} } )$ is independent of $K_{\rm MF}$.
Further information about the considered input pulses
All data are without consideration of the delay $\tau_g$.
(1) Rectangular Pulse
- The pulse $g(t)$ has constant height $A_g$ in the range $\pm \Delta t_g/2$ and is zero outside.
- The spectral function $G(f)=A_g\cdot \Delta t_g \cdot {\rm si}(\pi\cdot \Delta t_g \cdot f)$ has zeros at equidistant distances $1/\Delta t_g$.
- The pulse energy is $E_g=A_g^2\cdot \Delta t_g$.
(2) Gaussian Pulse
- The pulse $g(t)=A_g\cdot {\rm e}^{-\pi\cdot(t/\Delta t_g)^2}$ is infinitely extended. The maximum is $g(t= 0)=A_g$.
- The smaller the equivalent time duration $\Delta t_g$, the broader and lower the spectrum $G(f)=A_g \cdot \Delta t_g \cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot\hspace{0.05cm}(f\hspace{0.05cm}\cdot\hspace{0.05cm} \Delta t_g)^2}$.
- The pulse energy is $E_g=A_g^2\cdot \Delta t_g/\sqrt{2}$.
(3) Exponential Pulse
- The pulse is identically zero for $t<0$ and infinitely extended for positive times ⇒ $g(t)=A_g\cdot {\rm e}^{-t/\Delta t_g}$.
- $g(t)$ is (strongly) asymmetric ⇒ the spectrum $G(f)=A_g \cdot \Delta t_g/( 1 + {\rm j} \cdot 2\pi \cdot f \cdot \Delta t_g)$ is complex-valued;
- The pulse energy is $E_g=A_g^2\cdot \Delta t_g/2$.
Further information on the considered impulse responses
The different receiver filters $H(f)$ are described by their impulse responses $h(t)$.
Similar to the input pulses $g(t)$, these are characterized by the pulse height $A_h$, the equivalent pulse duration $\Delta t_h$ and the delay $\tau_h$ compared to the symmetrical case. The following short descriptions are always valid for $\tau_h= 0$.
(1) Slit lowpass ⇒ "rectangular impulse response"
- The impulse response $h(t)$ has constant height $A_h$ in the range $\pm \Delta t_h/2$ and is zero outside.
- The frequency response $H(f)=K \cdot {\rm si}(\pi\cdot \Delta t_g \cdot f)$ has zeros at equidistant intervals $1/\Delta t_h$.
- For white noise, the noise variance at the filter output is: $\sigma_d^2= N_0/2 \cdot A_h^2 \cdot \Delta t_h$.
(2) Gaussian lowpass ⇒ "Gaussian impulse response"
- The impulse response $h(t)=A_h\cdot {\rm e}^{-\pi\cdot(t/\Delta t_h)^2}$ ist is infinitely extended. The maximum is $h(t= 0)=A_h$.
- The smaller the equivalent time duration $\Delta t_h$, the broader and lower the frequency response $H(f)=K \cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot\hspace{0.05cm}(f\hspace{0.05cm}\cdot\hspace{0.05cm} \Delta t_h)^2}$.
- For white noise, the noise variance at the filter output is: $\sigma_d^2= N_0/2 \cdot A_h^2 \cdot \Delta t_h/\sqrt{2}$.
(3) First order lowpass ⇒ "Exponentially decaying impulse response"
- The impulse response is identically zero for $t<0$ and infinitely extended for positive times ⇒ $h(t)=A_h\cdot {\rm e}^{-t/\Delta t_h}$.
- $h(t)$ is causal and (strongly) asymmetric. The frequency response $H(f)=A_g \cdot \Delta t_g/( 1 + {\rm j} \cdot 2\pi \cdot f \cdot \Delta t_g)$ is complex-valued.
- For white noise, the noise variance at the filter output is: $\sigma_d^2= N_0/4 \cdot A_h^2 \cdot \Delta t_h$.
(4) Lowpass 4" ⇒ "Impulse response mirror image of (3)"
- The impulse response is identically zero for $t>0$ and infinitely extended for negative times ⇒ $h(t)=A_h\cdot {\rm e}^{t/\Delta t_h}$ für $t<0$.
- The frequency response $H(f)$ is conjugate complex to the frequency response of the first order lowpass filter.
- The noise variance at the filter output is exactly the same for white noise as for the first order lowpass: $\sigma_d^2= N_0/4 \cdot A_h^2 \cdot \Delta t_h$.
Exercises
- First, select the number $(1,\ 2, \text{...} \ )$ of the task to be processed. The number $0$ corresponds to a "Reset": Same setting as at program start.
- A task description is displayed. The parameter values are adjusted. Solution after pressing "Show Solution".
- Both the input signal $x(t)$ and the filter impulse response $h(t)$ are normalized, dimensionless and energy-limited ("time-limited pulses").
- All times, frequencies, and power values are to be understood normalized, too.
(1) Let the input pulse be Gaussian with $A_g=1,\ \Delta t_g=1,\ \tau_g=1$. Which setting leads to the "Matched Filter"? What value has $10 \cdot \lg \ \rho_{\rm MF}$ with $N_0=0.01$?
- The Matched Filter must also have a Gaussian shape and it must hold: $\Delta t_h=\Delta t_g=1,\ \tau_h =\tau_g=1$ ⇒ $T_{\rm D} = \tau_h +\tau_g=2$.
- The (instantaneous) signal-to-noise power ratio at the Matched Filter output is $\rho _{\rm MF} = { {2 \cdot E_g } }/{ {N_0 } } \approx 141.4$ ⇒ $10 \cdot \lg \ \rho _{\rm MF} \approx 21.5$ dB.
- With no other filter than the Matched Filter this $\rm SNR$ (or an even better one) can be achieved ⇒ $10 \cdot \lg \ \rho _{d} \le 10 \cdot \lg \ \rho _{\rm MF}$.
(2) The "Matched Filter" on rectangular input pulse with $A_g=1,\ \Delta t_g=1,\ \tau_g=0$ is a rectangular-in-time low–pass ⇒ rectangular impulse response.
What value has $10 \cdot \lg \ \rho_{\rm MF}$ with $N_0=0.01$? Interpret all the graphs shown and the numerical results in different ways
- The MF parameters are $A_h=A_g=1, \ \Delta t_h=\Delta t_g=1,\ \tau_h =\tau_g=0$ ⇒ $T_{\rm D} = \tau_h +\tau_g=0$ ⇒ $\rho _{\rm MF} = 200$ ⇒ $10 \cdot \lg \ \rho _{\rm MF} \approx 23$ dB.
- The pulse energy is the integral over $g^2(t)$ ⇒ $E_g = A_g^2 \cdot \Delta t_g=1$ ⇒ $\rho _{\rm MF} = 2 \cdot E_g /N_0 =200$. $T_{\text{D, opt} }=0$ is implicitly considered here.
- Another equation is $\rho_d (T_{\rm D}) =d_{\rm S}^2 (T_{\rm D})/\sigma_d^2$. The noise variance can, for example, be calculated as the integral over $h^2(t)$ ⇒ $\sigma_d^2= N_0 \cdot \Delta t_h/2 = 0.005$.
- The useful detection signal $d_{\rm S} (t)= g(t) * h(t)$ has a triangular shape with the maximum $d_{\rm S} (T_{\rm D, \ opt} = 0 )= 1$ ⇒ $\rho_d (T_{\rm D, \ opt} = 0 ) = 200= \rho _{\rm MF}$.
(3) The settings of $(2)$ continue to apply, with the exception of $N_0=0.02 $ instead of $N_0=0.01$. What changes can be seen?
- The only difference is twice the noise variance $\sigma_d^2= 0.01$ ⇒ $\rho_d (T_{\rm D, \ opt} = 0 ) = 100= \rho _{\rm MF}$ ⇒ $10 \cdot \lg \rho_{\rm MF} =20$ dB.
(4) The settings of $(3)$ continue to apply, except $T_{\rm D} = 0.1 $ instead of $T_{\rm D, \ opt} = 0$. What is the effect of this non-optimal detection time?
- Now the useful signal value $d_{\rm S} (T_{\rm D} = 0.1 )= 0.9$ is smaller ⇒ $\rho_d (T_{\rm D} = 0.1 ) =0.9^2/0.01= 81< \rho _{\rm MF}$. There is a degradation of nearly $1$ dB.
- For the further tasks the optimal detection time $T_{\rm D, \ opt}$ is assumed, if not explicitly stated otherwise.
(5) The settings of $(3)$ apply again except for a lower impulse response $A_h = 0.8 $ instead of $A_h = 1$. Interpret the changes.
- With $A_h \ne A_g$ it is also a Matched Filter as long as $h(t)$ is equal in shape to $g(t)$ ⇒ $\rho _{\rm MF} = { {2 \cdot E_g } }/{ {N_0 } } =100$ ⇒ $10 \cdot \lg \rho _{\rm MF} =20$ dB.
- The equation $\rho_d (T_{\rm D}=0) =d_{\rm S}^2 (T_{\rm D}=0)/\sigma_d^2$ leads to the same result, since ${d_{\rm S}}^2 (T_{\rm D})$ and $\sigma_d^2$ are compared to $(3)$ each reduced by a factor $0. 8^2$.
(6) Compared to $(5)$ now the height of the input pulse $g(t)$ is increased from $A_g = 1$ to $A_g = 1. 25$. Does $h(t)$ describe a Matched Filter? What is the SNR $\rho_{\rm MF}$?
- Again, this is a Matched Filter, since $h(t)$ and $g(t)$ are equal in shape. With $E_g = 1.25^2$: $\rho _{\rm MF} = { {2 \cdot 1.25^2 } }/{ 0.02 } =156.25$ ⇒ $10 \cdot \lg \rho_{\rm MF} \approx 21.9$ dB.
- The higher value $21.9$ dB compared to $(5)$ is related to the fact that for the same noise variance $\sigma_d^2= 0.0064$ the useful detection sample is again ${d_{\rm S}} (T_{\rm D}) = 1$.
(7) We continue from the rectangle–rectangle combination with $A_h=A_g=1,\ \ \Delta t_h=\Delta t_g=1,\ \tau_h=\tau_g=0,\ N_0 =0.02,\ T_{\rm D}=0$.
Interpret the results after varying the equivalent pulse duration $\Delta t_h$ of $h(t)$ in the range $0.6$ ... $1.4$. Use the graph representation over $\Delta t_h$.
- As expected the optimum is obtained for the equivalent pulse duration $\Delta t_h=\Delta t_g=1$. Then $10 \cdot \lg \ \rho_d (T_{\rm D, \ opt} = 0 ) =20$ dB $\big(= 10 \cdot \lg \rho_{\rm MF}\big)$.
- If $\Delta t_h<\Delta t_g=1$, the useful detection signal is trapezoidal. For $\Delta t_h=0.6$: $d_{\rm S} (T_{\rm D}=0)= 0.6$, $\sigma_d^2\approx0.006$ ⇒ $10 \cdot \lg \ \rho_d (T_{\rm D, \ opt} = 0 ) \approx 17.8$ dB.
- Also for $\Delta t_h>1$ the useful detection signal is trapezoidal, but now still $d_{\rm S} (T_{\rm D}=0)= 1$. The noise variance $\sigma_d^2$ increases continuously with $\Delta t_h$.
- For $\Delta t_h=1.4$: $\sigma_d^2=0.014$ ⇒ $10 \cdot \lg \ \rho_d (T_{\rm D, \ opt} = 0 ) \approx 18. 5$ dB. Compared to the Matched Filter $(\Delta t_h=1)$ the degradation is approx. $1.5$ dB.
(8) Now interpret the results for different $\Delta t_g$ of the input pulse $g(t)$ in the range $0.6$ ... $1.4$. Use the graph representation over $\Delta t_g$.
- Note: The blue curve $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt} )$ is the difference between $20\cdot \lg \ \big [{K \cdot d_{\rm S}} (T_{\rm D,\ opt}) \big ]$ (purple curve) and $20\cdot \lg \ \big [K \cdot \sigma_d \big ]$ (green curve).
- For the considered parameter set and $K=10$ the "green term" $20\cdot \lg \ \big [K \cdot \sigma_d \big ] = 0$ dB for all $\Delta t_g$ ⇒ the blue and the purple curves are identical.
- The blue curve $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt} )$ increases from $15.6$ dB $($for $\Delta t_g = 0. 6)$ to $20$ dB $($for $\Delta t_g = 1)$ continuously and then remains constant for $\Delta t_g > 1$.
- But, the setting $(\Delta t_g = 1.4,\ \Delta t_h = 1)$ does not yield a "Matched Filter". Rather, with $\Delta t_h = \Delta t_g = 1.4$: $10 \cdot \lg \ \rho_{\rm MF}=10 \cdot \lg \ (2 \cdot E_g/N_0) \approx 21.5$ dB.
- On the other hand the plot over $\Delta t_h$ with the default setting $(\Delta t_g = 1.4,\ \Delta t_h = 1)$ shows a monotonic increase of the blue curve $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt} )$.
- For $\Delta t_h = 0.6$ this gives $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt} )\approx 17.8$ dB, and for $\Delta t_h = 1. 4$ against $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt} )\approx 21.5$ dB $=10 \cdot \lg \ \rho_{\rm MF}$.
(9) We consider the exponential pulse $g(t)$ and the first order low–pass, where $A_h=A_g=1,\ \Delta t_h=\Delta t_g=1,\ \tau_h=\tau_g=0,\ N_0 =0.02,\ T_{\rm D}=1$.
Does this setting meet the Matched Filter criteria? Justify your answers with as many arguments as possible.
- No! Here $h(t)=g(t)$. In a Matched Filter configuration, the impulse response should be $h(t)={\rm const.}\cdot g(T_{\rm D}-t) $.
- The useful detection signal $d_{\rm S}(t)$ does not have a symmetric shape around the maximum. For the Matched Filter, $d_{\rm S}(T_{\rm D}-t) = d_{\rm S}(T_{\rm D}+t) $ would have to hold.
- Despite $\Delta t_h=\Delta t_g$ the SNR $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt}) \approx 14. 3$ dB is now less than $10 \cdot \lg \ \rho _{\rm MF} = 10 \cdot \lg \ 2 \cdot E_g/N_0 \approx 17$ dB.
(10) With all other settings being the same, what changes with the "extremely acausal filter"? Does the setting meet the Matched Filter criteria? Reason.
- Now here $h(t)=g(-t)$ and the useful detection signal $d_{\rm S}(t)$ is symmetric around $t=0$. It makes sense to choose $T_{\rm D} = 0 $ here.
- This gives $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt}) =10 \cdot \lg \ d_{\rm S}^2 (T_{\rm D,\ opt})/\sigma_d^2 = 17$ dB – the same value as for $10 \cdot \lg \ \rho _{\rm MF} = 10 \cdot \lg \ 2 \cdot E_g/N_0 = 17$ dB.
- The useful detection signal $d_{\rm S}(t)$ is of the same shape as the energy ACF of the input pulse $g(t)$. The Matched Filter focuses the energy around the time $T_{\rm D,\ opt}$.
(11) With which rectangular pulse $g(t)$ can one achieve the same $\rho _{\rm MF}=50$ as in task $(10)$?
With $(A_h=A_g=1,\ \ \Delta t_h=\Delta t_g=0.5)$ or with $(A_h=A_g=0.5,\ \ \Delta t_h=\Delta t_g=1)$ ?
- From the equation $\rho _{\rm MF} = 2 \cdot E_g/N_0$ it is already clear that the SNR depends only on the energy $E_g$ of the input pulse and not on its shape.
- The exponential pulse with $(A_g=1,\ \Delta t_g=1)$ has the energy $E_g=0.5$ ⇒ $\rho _{\rm MF}=50$. As well as the rectangular pulse with $(A_g=1,\ \Delta t_g=0.5)$.
- In contrast, the rectangular pulse with $(A_g=0.5,\ \Delta t_g=1)$ has a smaller energy ⇒ $E_g=0. 25$ ⇒ $\rho _{\rm MF}=25$ ⇒ $10 \cdot \lg \ \rho _{\rm MF} = 14$ dB.
Applet Manual
(A) Selection of the input pulse $g(t)$:
Rectangle | Gaussian | Exponential
(B) Parameter selection of the input pulse:
amplitude $A_g$, equivalent pulse duration $\Delta t_g$,
shift $\tau_g$
(C) Selection of the receiver filter impulse response $h(t)$:
rectangular-in-time | Gaussian low-pass |
1st order low-pass | extremely acausal filter
(D) Parameterwahl der Impulsantwort:
amplitude $A_h$, equivalent pulse duration $\Delta t_h$,
shift $\tau_g$, detection time $T_{\rm D}$
(E) Sketches of $g(t)$ $($red$)$ and $h(t)$ $($blue$)$
(F) Sketch of the convolution result $d_{\rm S}= g(t)\star h(t)$
(G) Input of the one-sided noise power density $N_0$
(H) Selection whether in area (K) the simulation results
should be displayed numerically or graphically
( I ) Display area for $h(t)^2$
(J) Display area for $|H(f)|^2$
(K) Area for numerical or graphical output
(L) Area for exercises: Task selection
(M) Area for exercises: Questions, sample solution
About the Authors
This interactive calculation tool was designed and implemented at the Institute for Communications Engineering at the Technical University of Munich.
- The first version was created in 2006 by Markus Elsberger as part of his bachelor thesis with “FlashMX – Actionscript” (Supervisor: Günter Söder).
- Last revision and English version 2020/2021 by Carolin Mirschina in the context of a working student activity.
The conversion of this applet to HTML 5 was financially supported by Studienzuschüsse ("study grants") of the TUM Faculty EI. We thank.