Applets:Physical Signal & Equivalent Lowpass Signal
Contents
Applet Description
This applet shows the relationship between the physical bandpass–signal $x(t)$ and the associated equivalent low pass–signal $x_{\rm TP}(t)$. The starting point is always a bandpass–signal $x(t)$ with a frequency-discrete spectrum $X(f)$:
- $$x(t) = x_{\rm T}(t) + x_{\rm O}(t) + x_{\rm U}(t) = A_{\rm T}\cdot \cos\left(2\pi f_{\rm T}\cdot t- \varphi_{\rm T}\right)+A_{\rm O}\cdot \cos\left(2\pi f_{\rm O}\cdot t- \varphi_{\rm O}\right)+ A_{\rm U}\cdot \cos\left(2\pi f_{\rm U}\cdot t- \varphi_{\rm U}\right). $$
The physical signal $x(t)$ is thus composed of three harmonic oscillations, a constellation which, for example, in the double-sideband amplitude modulation of the message signal $x_{\rm N}(t) = A_{\rm N}\cdot \cos\left(2\pi f_{\rm N}\cdot t- \varphi_{\rm N}\right)$ with the carrier signal $x_{\rm T}(t) = A_{\rm T}\cdot \cos\left(2\pi f_{\rm T}\cdot t - \varphi_{\rm T}\right)$ returns. The nomenclature is also adapted to this case:
- $x_{\rm O}(t)$ denotes the „upper sideband” with the amplitude $A_{\rm O}= A_{\rm N}/2$, the frequency $f_{\rm O} = f_{\rm T} + f_{\rm N}$ and the phase $\varphi_{\rm O} = \varphi_{\rm T} + \varphi_{\rm N}$.
- Similarly, for the „lower Sideband” $x_{\rm U}(t)$ with $f_{\rm U} = f_{\rm T} + f_{\rm N}$, $A_{\rm U}= A_{\rm O}$ and $\varphi_{\rm U} = -\varphi_{\rm O}$.
The corresponding equivalent low-pass–signal is $f_{\rm O}\hspace{0.01cm}' = f_{\rm O}- f_{\rm T} > 0$, $f_{\rm U}\hspace{0.01cm}' = f_{\rm U}- f_{\rm T} < 0$ and $f_{\rm T}\hspace{0.01cm}' = 0$:
- $$x_{\rm TP}(t) = x_\text{TP, T}(t) + x_\text{TP, O}(t) + x_\text{TP, U}(t) = A_{\rm T}\cdot {\rm e}^{-{\rm j} \varphi_{\rm T} } \hspace{0.1cm}+ \hspace{0.1cm} A_{\rm O}\cdot {\rm e}^{-{\rm j} \varphi_{\rm O} } \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm O}\hspace{0.01cm}'\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm}+ \hspace{0.1cm} A_{\rm U}\cdot {\rm e}^{-{\rm j} \varphi_{\rm U} } \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm U}\hspace{0.01cm}'\hspace{0.05cm}\cdot \hspace{0.05cm}t} . $$
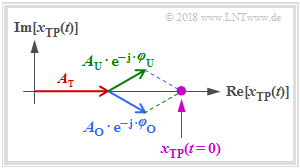
The program shows $x_{\rm TP}(t)$ as the vectorial sum of three rotation pointers as a violet point (see example graph for start time $t=0$ and cosinusoidal support):
- The (red) pointer of the carrier $x_\text{TP, T}(t)$ with the length $A_{\rm T}$ and the zero phase position $\varphi_{\rm T}=0$ lies in the complex plane firmly. So it applies to all times $t$: $x_{\rm TP}(t)= A_{\rm T}\cdot {\rm e}^{-{\rm j} \varphi_{\rm T} }$.
- The (blue) pointer of the upper sideband $x_\text{TP, O}(t)$ with the length $A_{\rm O}$ and the zero phase position $\varphi_{\rm O}$ rotates at the angular velocity $2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm O}\hspace{0.01cm}'$ in mathematically positive direction (one revolution in time $1/f_{\rm O}\hspace{0.01cm}')$.
- The (green) pointer of the lower sideband $x_{\rm U+}(t)$ with the length $A_{\rm U}$ and the zero phase position $\varphi_{\rm U}$ rotates at the angular velocity $2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm U}\hspace{0.01cm}'$, because of $f_{\rm U}\hspace{0.01cm}'<0$ counterclockwise.
- With $f_{\rm U}\hspace{0.01cm}' = -f_{\rm O}\hspace{0.01cm}'$ the blue and green pointers will spin at the same speed but in different directions. Also, if $A_{\rm O} = A_{\rm U}$ and $\varphi_{\rm U} = -\varphi_{\rm O}$, then $x_{\rm TP}(t)$ on a line with a slope of $\varphi_{\rm T}$.
Hinweis: The graphic applies to $\varphi_{\rm O} = +30^\circ$. From this follows for the start time $t=0$ the angle of the blue pointer (OSB) with respect to the coordinate system: $\phi_{\rm O} = -\varphi_{\rm O} = -30^\circ$. Likewise, the null phantom $\varphi_{\rm U} = -30^\circ$ of the lower sideband (USB, grüner Zeiger) follows for the phase angle to be considered in the complex plane: $\phi_{\rm U} = +30^\circ$.
The temporal course of $x_{\rm TP}(t)$ is also referred to below as locus. The relationship between $x_{\rm TP}(t)$ and the physical bandpass –signal $x(t)$ is given in the section ??? and the associated analytic signal is $x_+(t)$ :
- $$x_{\rm TP}(t) = x_{\rm +}(t)\cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi \cdot f_{\rm T}\cdot \hspace{0.05cm}t},$$
- $$x_{\rm +}(t) = x_{\rm TP}(t)\cdot {\rm e}^{+{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi \cdot f_{\rm T}\cdot \hspace{0.05cm}t}.$$
Theoretical Background
Description of Bandpass Signals
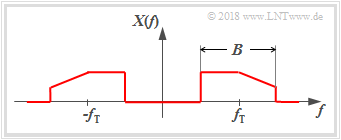
We consider bandpass signals $x(t)$ with the property that their spectra $X(f)$ are not in the range around the frequency $f=0$, but around a carrier frequency $f_{\rm T}$. In most cases it can also be assumed that the bandwidth is $B \ll f_{\rm T}$.
The figure shows such a bandpass spectrum $X(f)$. Assuming that the associated $x(t)$ is a physical signal and thus real, the spectral function $X(f)$ has a symmetry with respect to the frequency $f = 0$, if $x(t)$ is an even function ⇒ $x(-t)=x(t)$, $X(f)$ is real and even.
Beside the physical signal $x(t)\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X(f)$, one can also use the following descriptions of bandpass signals:
- the analytic signal $x_+(t)\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X_+(f)$, see applet Physikalisches Signal & Analytisches Signal,
- the equivalent low-pass–signal $x_{\rm TP}(t)\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X_{\rm TP}(f)$, see next page
Spectral Functions of the Analytic and the Equivalent Low-Pass Signal
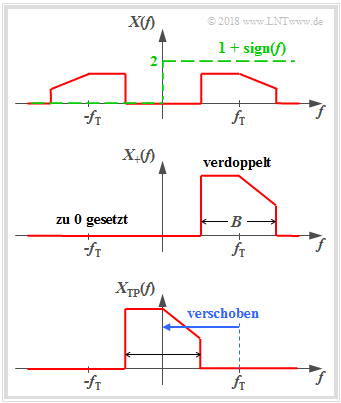
The analytische Signal $x_+(t)$ belonging to the physical signal $x(t)$ is the time function whose spectrum fulfills the following property:
- $$X_+(f)=\big[1+{\rm sign}(f)\big] \cdot X(f) = \left\{ {2 \cdot X(f) \; \hspace{0.2cm}\rm for\hspace{0.2cm} {\it f} > 0, \atop {\,\,\,\, \rm 0 \; \hspace{0.9cm}\rm for\hspace{0.2cm} {\it f} < 0.} }\right.$$
The Signumfunktion is for positive values of $f$ equal to $+1$ and for negative $f$ values equal to $-1$.
- The (double-sided) limit returns $\sign(0) = 0$.
- The index „+” should make it clear that $X_+(f)$ only has parts at positive frequencies.
From the graph you can see the calculation rule for $X_+(f)$:
The actual BP spectrum $X(f)$ becomes
- doubled at the positive frequencies, and
- set to zero at the negative frequencies.
Due to the asymmetry of $X_+(f)$ with respect to the frequency $f = 0$, it can already be said that the time function $x_+(t)$ except for a trivial special case $x_+(t)= 0 \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\ \ X_+(f)= 0$ is always complex.
The spectrum $X_{\rm TP}(f)$ of the equivalent low-pass signal is obtained by shifting $X_+(f)$ to the left by the carrier frequency $f_{\rm T}$:
- $$X_{\rm TP}(f)= X_+(f+f_{\rm T}).$$
In the time domain this operation corresponds to the multiplication of $x_{\rm +}(t)$ with the complex exponential function with negative exponent:
- $$x_{\rm TP}(t) = x_{\rm +}(t)\cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi \cdot f_{\rm T}\cdot \hspace{0.05cm}t}.$$
It can be seen that $x_{\rm TP}(t)$ s generally complex. But if $X_+(f)$ is symmetric about the carrier frequency $f_{\rm T}$, $X_{\rm TP}(f)$ is symmetric about the frequency $f=0$ and the result is accordingly real time function $x_{\rm TP}(t)$.
$x_{\rm TP}(t)$–Representation of a Sum of Three Harmonic Oscillations
In our applet, we always assume a set of three rotating pointers. The physical signal is:
- $$x(t) = x_{\rm U}(t) + x_{\rm T}(t) + x_{\rm O}(t) = A_{\rm U}\cdot \cos\left(2\pi f_{\rm U}\cdot t- \varphi_{\rm U}\right)+A_{\rm T}\cdot \cos\left(2\pi f_{\rm T}\cdot t- \varphi_{\rm T}\right)+A_{\rm O}\cdot \cos\left(2\pi f_{\rm O}\cdot t- \varphi_{\rm O}\right). $$
- Each of the three harmonic oscillations $x_{\rm T}(t)$, $x_{\rm U}(t)$ and $x_{\rm O}(t)$ is represented by an amplitude $(A)$, a frequency $(f)$ and a phase value $(\varphi)$.
- The indices are based on the modulation method double sideband –amplitude modulation. „T” stands for „carrier”, „U” for „lowei sideband” and „O” for „upper Sideband”. Similarly, $f_{\rm U} < f_{\rm T}$ and $f_{\rm O} > f_{\rm T}$. There are no restrictions for the amplitudes and phases.
The associated equivalent low-pass signal is with $f_{\rm O}\hspace{0.01cm}' = f_{\rm O}- f_{\rm T} > 0$, $f_{\rm U}\hspace{0.01cm}' = f_{\rm U}- f_{\rm T} < 0$ and $f_{\rm T}\hspace{0.01cm}' = 0$:
- $$x_{\rm TP}(t) = x_\text{TP, T}(t) + x_\text{TP, O}(t) + x_\text{TP, U}(t) = A_{\rm T}\cdot {\rm e}^{-{\rm j} \varphi_{\rm T} } \hspace{0.1cm}+ \hspace{0.1cm} A_{\rm O}\cdot {\rm e}^{-{\rm j} \varphi_{\rm O} } \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm O}\hspace{0.01cm}'\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm}+ \hspace{0.1cm} A_{\rm U}\cdot {\rm e}^{-{\rm j} \varphi_{\rm U} } \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm U}\hspace{0.01cm}'\hspace{0.05cm}\cdot \hspace{0.05cm}t} . $$
$\text{Example 1:}$ The constellation given here results, for example, in the double sideband amplitude modulation of the message signal $x_{\rm N}(t) = A_{\rm N}\cdot \cos\left(2\pi f_{\rm N}\cdot t- \varphi_{\rm N}\right)$ with the carrier signal $x_{\rm T}(t) = A_{\rm T}\cdot \cos\left(2\pi f_{\rm T}\cdot t - \varphi_{\rm T}\right)$. This is discussed more frequently in the experimental procedure.
There are some limitations to the program parameters in this approach:
- The frequencies are always $f\hspace{0.05cm}'_{\rm O} = f_{\rm N}$ and $f\hspace{0.05cm}'_{\rm U} = -f_{\rm N}$.
- Without distortion, the amplitude of the sidebands is $A_{\rm O}= A_{\rm U}= A_{\rm N}/2$.
- The respective phase relationships can be seen from the graph.
Representation of the Equivalent Low-Pass Signal by Magnitude and Phase
The generally complex valued equivalent low-pass signal
- $$x_{\rm TP}(t) = a(t) \cdot {\rm e}^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \phi(t) }$$
can be split into a magnitude function $a(t)$ and a phase function $\phi(t)$ according to the equation given here, where:
- $$a(t) = \vert x_{\rm TP}(t)\vert = \sqrt{ {\rm Re}^2\big [x_{\rm TP}(t)\big ] + {\rm Im}^2\big [x_{\rm TP}(t)\big ] }\hspace{0.05cm},$$
- $$\phi(t) = \text{arc }x_{\rm TP}(t) = \arctan \frac{{\rm Im}\big [x_{\rm TP}(t)\big ]}{{\rm Re}\big [x_{\rm TP}(t)\big ]}.$$
The reason that a bandpass–signal $x(t)$ is usually described by the equivalent low-pass signal $x_{\rm TP}(t)$ is that the functions $a(t)$ and $\phi(t)$ are interpretable in both representations:
- The amount $a(t)$ of the equivalent low-pass signal $x_{\rm TP}(t)$ indicates the (time-dependent) envelope of $x(t)$.
- The phase $\phi(t)$ of $x_{\rm TP}(t)$ denotes the location of the zero crossings of $x(t)$, where:
- – For $\phi(t)>0$ the zero crossing is earlier than its nominal position ⇒ the signal is leading here.
- – When $\phi(t)<0$, the zero crossing is later than its target position ⇒ the signal is trailing here.
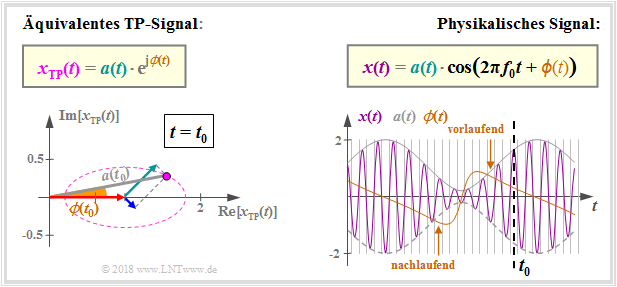
$\text{Example 2:}$ The graph is intended to illustrate this relationship, assuming $A_{\rm U} > A_{\rm O}$ ⇒ the green pointer (for the lower sideband) is longer than the blue pointer (upper sideband). This is a snapshot at time $t_0$:
- For these system parameters, the top of the pointer cluster $x_{\rm TP}(t)$ – that is, the geometric sum of red, blue and green pointers – on an ellipse.
- The amount $a(t_0) = \vert x_{\rm TP}(t_0) \vert$ is drawn in black in the left-hand diagram and the phase value $\phi(t_0) = \text{arc }x_{\rm TP}(t_0) > 0$ is indicated in brown color.
- In the graph on the right, the amount $a(t_0) = \vert x_{\rm TP}(t_0) \vert$ of the equivalent low-pass signal indicates the envelope of the physical signal $x(t)$.
- At $\phi(t) \equiv 0$, all zero crossings of $x(t)$ would occur at equidistant intervals. Because of $\phi(t_0) > 0$, the signal is leading at the time $t_0$, that is: the zero crossings come earlier than the grid dictates.
Exercises
- First select the task number.
- A task description is displayed.
- Parameter values are adjusted.
- Solution after pressing „Hide solition”.
The number „0” will reset the program and output a text with the further explanation of the applet.
In the following, $\rm Green$ denotes the lower sideband ⇒ $\big (A_{\rm U}, f_{\rm U}, \varphi_{\rm U}\big )$,
$\rm Red$ the carrier ⇒ $\big (A_{\rm T}, f_{\rm T}, \varphi_{\rm T}\big )$ and
$\rm Blue$ the upper sideband ⇒ $\big (A_{\rm O}, f_{\rm O}, \varphi_{\rm O}\big )$.
(1) Let $\text{Red:} \hspace{0.15cm} A_{\rm T} = 1\ \text{V}, f_{\rm T} = 100 \ \text{kHz}, \varphi_{\rm T} = 0^\circ$, $\text{Green:} \hspace{0.15cm} A_{\rm U} = 0.4 \text{V}, \ f_{\rm U} = 80 \ \text{kHz}, \varphi_{\rm U} = -90^\circ$, $\text{Blue:} \hspace{0.15cm} A_{\rm O} = 0.4\ \text{V}, f_{\rm O} = 120 \ \text{kHz}, \varphi_{\rm O} = 90^\circ$.
- Consider and interpret the equivalent low-pass signal $x_{\rm TP}(t)$ and the physical signal $x(t)$. Which period $T_0$ does one recognize?
- The equivalent low-pass signal $x_{\rm TP}(t)$ takes from $x_{\rm TP}(t=0)=1\ \text{V}$ on the real axis values between $0.2\ \text{V}$ and $1.8\ \text{V}$ ⇒ phase $\phi(t) \equiv 0$.
The amount $|x_{\rm TP}(t)|$ indicates the envelope $a(t)$ of the physical signal $x(t)$. It holds $A_{\rm N} = 0.8\ \text{V}$ and $f_{\rm N} = 20\ \text{kHz}$: $a(t) = A_{\rm T}+ A_{\rm N} \cdot \sin(2\pi\cdot f_{\rm N} \cdot t)$.
Both $x_{\rm TP}(t)$ and $x(t)$ are periodic with the period $T_0 = 1/f_{\rm N} = 50\ \rm µ s$.
- The equivalent low-pass signal $x_{\rm TP}(t)$ takes from $x_{\rm TP}(t=0)=1\ \text{V}$ on the real axis values between $0.2\ \text{V}$ and $1.8\ \text{V}$ ⇒ phase $\phi(t) \equiv 0$.
(2) How do the ratios change to (1) with $f_{\rm U} = 99 \ \text{kHz}$ and $f_{\rm O} = 101 \ \text{kHz}$ ? How could $x(t)$ have arisen?
- For the envelope $a(t)$ of the signal $x(t)$ we still have $a(t) = A_{\rm T}+ A_{\rm N} \cdot \sin(2\pi\cdot f_{\rm N} \cdot t)$, but now $f_{\rm N} = 1\ \text{kHz}$. Even though it can not be recognized:
$x_{\rm TP}(t)$ and $x(t)$ are still periodic: $T_0 = 1\ \rm ms$. Example: Double sideband - Amplitude modulation (ZSB–AM) of a sine signal with cosine–carrier.
- For the envelope $a(t)$ of the signal $x(t)$ we still have $a(t) = A_{\rm T}+ A_{\rm N} \cdot \sin(2\pi\cdot f_{\rm N} \cdot t)$, but now $f_{\rm N} = 1\ \text{kHz}$. Even though it can not be recognized:
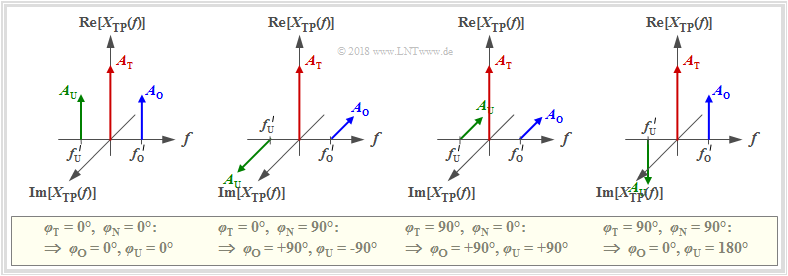
(3) Which settings have to be changed from (2) in order to arrive at the ZSB–AM of a cosine signal with sine–carrier. What changes over (2)?
- The carrier phase must be changed to $\varphi_{\rm T} = 90^\circ$ ⇒ sine–carrier. Similarly, $\varphi_{\rm O} =\varphi_{\rm U} =\varphi_{\rm T} = 90^\circ$ must be set ⇒ cosine-shaped message
The locus now lies on the imaginary axis ⇒ $\phi(t) \equiv -90^\circ$. At the beginning we have $x_{\rm TP}(t=0)= - {\rm j} \cdot 1.8 \ \text{V}$.
- The carrier phase must be changed to $\varphi_{\rm T} = 90^\circ$ ⇒ sine–carrier. Similarly, $\varphi_{\rm O} =\varphi_{\rm U} =\varphi_{\rm T} = 90^\circ$ must be set ⇒ cosine-shaped message
(4) Now let $\text{Red:} \hspace{0.15cm} A_{\rm T} = 1\ \text{V}, \ f_{\rm T} = 100 \ \text{kHz}, \ \varphi_{\rm T} = 0^\circ$, $\text{Green:} \hspace{0.15cm} A_{\rm U} = 0.4 \text{V}, \ f_{\rm U} = 80 \ \text{kHz}, \ \varphi_{\rm U} = 0^\circ$, $\text{Blue:} \hspace{0.15cm} A_{\rm O} = 0.4\ \text{V}, \ f_{\rm O} = 120 \ \text{kHz}, \ \varphi_{\rm O} = 0^\circ$.
- What are the characteristics of this system „ZSB–AM, where the message signal and carrier are respectively cosinusoidal”? What is the modulation depth $m$?
- The equivalent low-pass signal $x_{\rm TP}(t)$ takes from $x_{\rm TP}(t=0)=1.8\ \text{V}$ on the real axis values between $0.2\ \text{V}$ and $1.8\ \text{V}$ ⇒ phase $\phi(t) \equiv 0$.
Except for the start state $x_{\rm TP}(t=0)$ same behavior as with the setting (1). The modulation depth is $m = 0.8$.
- The equivalent low-pass signal $x_{\rm TP}(t)$ takes from $x_{\rm TP}(t=0)=1.8\ \text{V}$ on the real axis values between $0.2\ \text{V}$ and $1.8\ \text{V}$ ⇒ phase $\phi(t) \equiv 0$.
(5) The parameters are still valid according to (4) with the exception of $A_{\rm T}= 0.6 \text{V}$. How big is the degree of modulation $m$? What are the consequences?
- There is now a ZSB–AM with modulation degree $m = 1.333$. For $m > 1$, the simpler envelope demodulation is not applicable, since the phase function $\phi(t) \in \{ 0, \ \pm 180^\circ\}$ is no longer constant and the envelope $a(t)$ no longer matches the message signal. Rather, the more complex synchronous demodulation must be used. Envelope detection would produce nonlinear distortions.
(6) The parameters are still valid according to (4) or (5) with the exception from $A_{\rm T}= 0$ on ⇒ $m \to \infty$. Which modulation method is described in this way?
- It is a ZSB–AM without carrier and requires synchronous demodulation. The equivalent low-pass signal $x_{\rm TP}(t)$ is on the real axis, but not only in the right half-plane. Thus, the phase function $\phi(t) \in \{ 0, \ \pm 180^\circ\}$, also applies here, which means that envelope demodulation is not applicable.
(7) Now let $\text{Red:} \hspace{0.15cm} A_{\rm T} = 1\ \text{V}, f_{\rm T} = 100 \ \text{kHz}, \varphi_{\rm T} = 0^\circ$, $\text{Green:} \hspace{0.15cm} A_{\rm U} = 0, \ f_{\rm U} = 80 \ \text{kHz}, \varphi_{\rm U} = -90^\circ$, $\text{Blue:} \hspace{0.15cm} A_{\rm O} = 0.8\ \text{V}, f_{\rm O} = 120 \ \text{kHz}, \varphi_{\rm O} = 90^\circ$.
- Which constellation is described here? Which characteristics of this procedure can be recognized from the graphic?
- It is a single-sideband modulation (ESB–AM), more specifically an OSB–AM: the red carrier is fixed, the green pointer missing and the blue pointer (OSB) turns counterclockwise. The degree of modulation is $\mu = 0.8$ (in the case of ESB we denote the degree of modulation with $\mu$ instead of $m$). The carrier signal is cosinusoidal and the message signal sinusoidal.
The locus is a circle. $x_{\rm TP}(t)$ moves in a mathematically positive direction. Because of $\phi(t) \ne \text{const.}$, The envelope demodulation is not applicable here: This can be seen by the fact that the envelope $a(t)$ is not cosinusoidal. Rather, the lower half-wave is sharper than the upper ⇒ strong linear distortions.
- It is a single-sideband modulation (ESB–AM), more specifically an OSB–AM: the red carrier is fixed, the green pointer missing and the blue pointer (OSB) turns counterclockwise. The degree of modulation is $\mu = 0.8$ (in the case of ESB we denote the degree of modulation with $\mu$ instead of $m$). The carrier signal is cosinusoidal and the message signal sinusoidal.
(8) The parameters are still valid according to (7) with the exception of $A_{\rm O}= 0$ and $A_{\rm U}= 0.8 \text{ V}$. What differences arise opposite (7)?
- Now it is a USB–AM: The red carrier is fixed, the blue pointer is missing and the green pointer (USB) rotates clockwise. All other statements of (7) apply here as well.
(9) The parameters according to (7) are still valid with the exception of $A_{\rm O} = 0.2 \text{ V} \ne A_{\rm U} = 0.4 \text{ V} $. What are the differences from (7)?
- The locus $x_{\rm TP}(t)$ is not a horizontal straight line, but an ellipse with the real part between $0.4 \text{ V}$ and $1.6 \text{ V}$ and the imaginary part in the range $\pm 0.2 \text{ V}$. Because of $\phi(t) \ne \text{const.}$ , Envelope demodulation would lead to non-linear distortions here too.
The constellation simulated here describes the situation of (4), namely a ZSB–AM with modulation degree $m = 0.8$, where the upper sideband is reduced to $50\%$ due to channel attenuation.
- The locus $x_{\rm TP}(t)$ is not a horizontal straight line, but an ellipse with the real part between $0.4 \text{ V}$ and $1.6 \text{ V}$ and the imaginary part in the range $\pm 0.2 \text{ V}$. Because of $\phi(t) \ne \text{const.}$ , Envelope demodulation would lead to non-linear distortions here too.
Applet Manual
- The red parameters $(A_{\rm T}, \ f_{\rm T}, \ \varphi_{\rm T})$ and the red pointer mark the Carrier. (German: Träger).
- The green parameters $(A_{\rm U}, \ f_{\rm U} < f_{\rm T}, \ \varphi_{\rm U})$ mark the Lower sideband. (German: Untere Seitenband).
- The blue parameters $(A_{\rm O}, \ f_{\rm O} > f_{\rm T}, \ \varphi_{\rm O})$ mark the Upper sideband. (German: Obere Seitenband).
- The red pointer does not turn.
- The green pointer rotates in a mathematically negative direction (clockwise).
- The blue pointer turns counterclockwise.
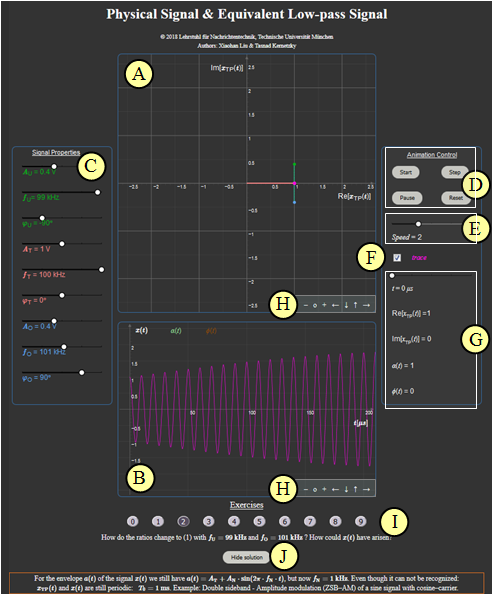
Meaning of the letters in the adjacent graphic:
(A) Plot of the equivalent low-pass Signal $x_{\rm TP}(t)$
(B) Plot of the physical signal $x(t)$
(C) Parameter input via slider: amplitudes, frequencies, phase values
(D) Control elements: Start – Step – Pause/Continue – Reset
(E) Speed of animation: „Speed” ⇒ Values: 1, 2 oder 3
(F) „Trace” ⇒ On or Off, trace of equivalent low-pass Signal $x_{\rm TP}(t)$
(G) Numerical output: time $t$, the signal values ${\rm Re}[x_{\rm TP}(t)]$ and ${\rm Im}[x_{\rm TP}(t)]$,
$\text{}\hspace{4.2cm}$ Hüllkurve $a(t) = |x_{\rm TP}(t)|$ und Phase $\phi(t) = {\rm arc} \ x_{\rm TP}(t)$
(H) Variations for the graphical representation
$\hspace{1.5cm}$Zoom–Functions „$+$” (Enlarge), „$-$” (Decrease) und $\rm o$ (Reset to default)
$\hspace{1.5cm}$Move with „$\leftarrow$” (Section to the left, ordinate to the right), „$\uparrow$” „$\downarrow$” „$\rightarrow$”
(I) Experiment section: Task selection and task
(J) Experiment section: solution
About the Authors
This interactive calculation was designed and realized at the Lehrstuhl für Nachrichtentechnik of the Technical University of Munich .
- The original version was created in 2005 by Ji Li as part of her Diploma thesis using „FlashMX–Actionscript” (Supervisor: Günter Söder).
- In 2018 this Applet was redesigned and updated to „HTML5” by Xiaohan Liu as part of her Bachelor's thesis (Supervisor: Tasnád Kernetzky).