The bit error probability
- $$p_{\rm B} = {1}/{2} \cdot{\rm erfc} \left( \sqrt{{E_{\rm B}}/{N_0}}\right)$$
of a binary system was simulatively determined by a measurement of the bit error rate $\rm (BER)$:
- $$h_{\rm B} = {n_{\rm B}}/{N}.$$
Often, $h_{\rm B}$ is also called "bit error frequency".
In above equations mean:
- $E_{\rm B}$: energy per bit,
- $N_0$: AWGN noise power density,
- $n_{\rm B}$: number of bit errors occurred,
- $N$: number of simulated bits of a test series.
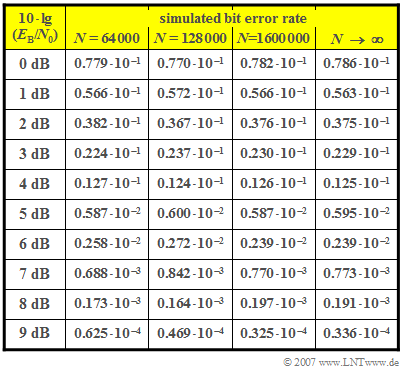
The table shows the results of some test series with $N = 6.4 \cdot 10^4 $, $N = 1. 28 \cdot 10^5$ and $N = 1.6 \cdot 10^6$. The last column named $N \to \infty $ gives the bit error probability $p_{\rm B}$.
The following properties are referred to in the exercise questionnaire:
- The bit error frequency $h_{\rm B}$ is (to a first approximation) a Gaussian distributed random variable with mean $m_h = p_{\rm B}$ and variance $\sigma_h^2 \approx p_{\rm B}/N$.
- The relative deviation of the bit error frequency from the probability is
- $$\varepsilon_{\rm rel}= \frac {h_{\rm B}-p_{\rm B}}{p_{\rm B}}\hspace{0.05cm}.$$
- As a rough rule of thumb on the required accuracy, the number of measured bit errors should be $n_{\rm B} \ge 100$.
Note:
- The exercise belongs to the chapter "Error Probability for Baseband Transmission".
Questions
Solution
- Of course, the accuracy of the BER measurement is influenced by the parameter $N$ to a large extent. On statistical average, the BER measurement naturally becomes better when $N$ is increased.
- However, there is no deterministic relationship between the number of simulated bits and the accuracy of the BER measurement, as shown, for example, by the results for $10 \cdot \lg \ E_{\rm B}/N_0 = 6 \ \rm dB$:
- For $N = 6.4 \cdot 10^4\ (h_{\rm B} = 0.258 \cdot 10^{-2})$, the deviation from the true value $(0.239 \cdot 10^{-2})$ is smaller than for $N = 1.28 \cdot 10^5\ (h_{\rm B} = 0.272 \cdot 10^{-2})$.
(2) At $10 \cdot \lg \ E_{\rm B}/N_0 = 0 \ \rm dB$, i.e. $E_{\rm B} = N_0$, the following values are obtained:
- $$N = 6.4 \cdot 10^4\text{:}\hspace{0.4cm}\sigma_h = \sqrt{{p}/{N}}= \sqrt{\frac{0.0786}{64000}}\hspace{0.1cm}\underline {\approx 1.1 \cdot10^{-3}}\hspace{0.05cm},$$
- $$N = 1.6 \cdot 10^6\text{:}\hspace{0.4cm} \sigma_h = \sqrt{{p}/{N}}= \sqrt{\frac{0.0786}{1600000}}\hspace{0.1cm}\underline {\approx 0.22 \cdot10^{-3}}\hspace{0.05cm}.$$
(3) For this, $10 \cdot \lg \ E_{\rm B}/N_0 = 0 \ \rm dB$ yields the following values:
- $$N = 6.4 \cdot 10^4\text{:}\hspace{0.4cm}\varepsilon_{\rm rel}= \frac{h_{\rm B}- p_{\rm B}}{h_{\rm B}} = \frac{0.0779-0.0786}{0.0786}\hspace{0.1cm}\underline {\approx -0.9\% }\hspace{0.05cm}$$
- $$N = 1.6 \cdot 10^6\text{:}\hspace{0.4cm} \varepsilon_{\rm rel}= \frac{h_{\rm B}- p_{\rm B}}{h_{\rm B}}= \frac{0.0782-0.0786}{0.0786}\hspace{0.1cm}\underline {\approx -0.5\% } \hspace{0.05cm}.$$
(4) Due to the smaller error probability, the values are now smaller than in subtask (2):
- $$N = 6.4 \cdot 10^4\text{:}\hspace{0.4cm}\sigma_h = \sqrt{{p}/{N}}= \sqrt{\frac{0.336 \cdot 10^{-4}}{6.4 \cdot 10^{4}}}\hspace{0.1cm}\underline {\approx 2.3 \cdot 10^{-5}}\hspace{0.05cm},$$
- $$ N = 1.6 \cdot 10^6\text{:}\hspace{0.4cm}\sigma_h = \sqrt{{p}/{N}}= \sqrt{\frac{0.336 \cdot 10^{-4}}{1.6 \cdot 10^{6}}}\hspace{0.1cm}\underline {\approx 0.46 \cdot10^{-5}}\hspace{0.05cm}.$$
(5) Despite the much smaller standard deviation $\sigma_h$, the smaller error probability results in larger relative deviations for $10 \cdot \lg \ E_{\rm B}/N_0 = 9 \ \rm dB$
than for $10 \cdot \lg \ E_{\rm B}/N_0 = 0 \ \rm dB$:
- $$N = 6.4 \cdot 10^4\text{:}\hspace{0.4cm}\varepsilon_{\rm rel}= \frac{h_{\rm B}- p_{\rm B}}{h_{\rm B}}= \frac{0.625 \cdot 10^{-4} - 0.336 \cdot 10^{-4}}{0.336 \cdot 10^{-4}}\hspace{0.1cm}\underline { \approx 86\% } \hspace{0.05cm},$$
- $$N = 1.6 \cdot 10^6\text{:}\hspace{0.4cm}\varepsilon_{\rm rel}= \frac{h_{\rm B}- p_{\rm B}}{h_{\rm B}}= \frac{0.325 \cdot 10^{-4} - 0.336 \cdot 10^{-4}}{0.336 \cdot 10^{-4}}\hspace{0.1cm}\underline {\approx -3.3\%}\hspace{0.05cm}.$$
(6) The number of measured bit errors should be $n_{\rm B} \ge 100$. Therefore, approximately (rounding errors should be taken into account):
- $$n_{\rm B} = {p_{\rm B}}\cdot {N} > 100 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm B} > \frac{100}{1.6 \cdot 10^6} = 0.625 \cdot 10^{-4}\hspace{0.05cm}.$$
- It further follows that in the simulation for $10 \cdot \lg \ E_{\rm B}/N_0\hspace{0.05cm}\underline{ = 8 \ \rm dB}$ still a sufficient number of bit errors occurred $(n_{\rm B} =1.6 \cdot 10^{6}\cdot 0.197 \cdot 10^{-3}= 315)$, while for $10 \cdot \lg \ E_{\rm B}/N_0 = 9 \ \rm dB$ on average only $n_{\rm B} =52$ errors are to be expected.
- For this dB value, about twice the number of bits would have to be simulated.