Exercise 2.6: Two-Way Channel
From LNTwww
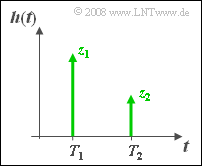
- Der so genannte Zweiwegekanal wird durch folgende Impulsantwort charakterisiert (mit T1 < T2):
- $$h(t) = z_1 \cdot \delta ( t - T_1) + z_2 \cdot \delta ( t - T_2).$$
- Bis auf wenige Kombinationen der Systemparameter z1, T1, z2 und T2 wird dieser Kanal zu linearen Verzerrungen führen. Man spricht nur dann von einem verzerrungsfreien Kanal, wenn durch ihn kein einziges Eingangssignal verzerrt wird. Das bedeutet: Auch bei einem verzerrenden Kanal kann es Sonderfälle geben, bei denen tatsächlich y(t) = α · x(t – τ) gilt.
- Als Testsignale werden an den Systemeingang angelegt:
- ein Diracpuls x1(t) im Zeitabstand T0 = 1 ms gemäß
- $$x_1(t) = \sum_{n = - \infty}^{+\infty} \delta ( t - n \cdot T_0) ,$$
- dessen Spektralfunktion ebenfalls ein Diracpuls ist, und zwar mit Abstand f0 = 1/T0 = 1 kHz:
- $$X_1(f) = T_0 \cdot \sum_{k = - \infty}^{+\infty} \delta ( f - k \cdot f_0) ,$$
- ein Cosinussignal mit der Frequenz f2 = 250 Hz:
- $$x_2(t) = \cos(2 \pi \cdot f_2 \cdot t) ,$$
- die Summe zweier Cosinussignale mit den Frequenzen f2 = 250 Hz und f3 = 1250 Hz:
- $$x_3(t) = \cos(2 \pi \cdot f_2 \cdot t) + \cos(2 \pi \cdot f_3 \cdot t) .$$
- Hinweis: Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 2.3. Um Ihnen einige Rechnungen zu ersparen, wird folgendes Ergebnis für den Parametersatz z1 = 1, T1 = 0, z2 = 0.5 und T2 = 1 ms vorweggenommen:
- $$|H(f = f_2)| = |H(f = f_3)| = \sqrt{1.25} \hspace{0.45cm} \approx 1.118, \\ b(f = f_2) = b(f = f_3) = \arctan (0.5) \approx 0.464.$$
Fragebogen
Musterlösung
1.
2.
3.
4.
5.
6.
7.