Exercise 2.7Z: Huffman Coding for Two-Tuples of a Ternary Source
From LNTwww
(Redirected from Aufgabe 2.7Z: Huffman-Codierung für Zweiertupel einer Ternärquelle)
We consider the same situation as in Exercise A2.7:
- The Huffman algorithm leads to a better result, i.e. to a smaller average code word length $L_{\rm M}$, if one does not apply it to individual symbols but forms $k$–tuples beforehand.
- This increases the symbol set size from $M$ to $M\hspace{0.03cm}' = M^k$.
For the message source considered here, the following applies:
- Symbol set size: $M = 3$,
- Symbol set: $\{$ $\rm X$, $\rm Y$, $\rm Z$ $\}$,
- Probabilities: $p_{\rm X} = 0.7$, $p_{\rm Y} = 0.2$, $p_{\rm Z} = 0.1$,
- Entropy: $H = 1.157 \ \rm bit/ternary\hspace{0.12cm}symbol$.
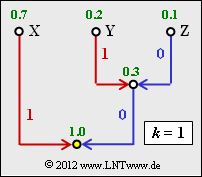
The graph shows the Huffman tree when the Huffman algorithm is applied to single symbols $(k= 1)$.
In subtask (2) you are to give the corresponding Huffman code when two-tuples are formed beforehand $(k=2)$.
Hints:
- The exercise belongs to the chapter Entropy Coding according to Huffman.
- In particular, reference is made to the page Application of Huffman coding to $k$-tuples.
- A comparable task with binary input symbols is dealt with in Exercise 2.7 .
- Designate the possible two-tuples with $\rm XX = A$, $\rm XY = B$, $\rm XZ = C$, $\rm YX = D$, $\rm YY = E$, $\rm YZ = F$, $\rm ZX = G$, $\rm ZY = H$, $\rm ZZ = I$.
Questions
Solution
(1) The average code word length is with $p_{\rm X} = 0.7$, $L_{\rm X} = 1$, $p_{\rm Y} = 0.2$, $L_{\rm Y} = 2$, $p_{\rm Z} = 0.1$, $L_{\rm Z} = 2$:
- $$L_{\rm M} = p_{\rm X} \cdot 1 + (p_{\rm Y} + p_{\rm Z}) \cdot 2 \hspace{0.15cm}\underline{= 1.3\,\,{\rm bit/source\:symbol}}\hspace{0.05cm}. $$
- This value is greater than the source entropy $H = 1.157$ bit/source symbol.
(2) There are $M\hspace{0.03cm}' = M^k = 3^2 = 9$ two-tuples with the following probabilities:
- $$p_{\rm A} = \rm Pr(XX) = 0.7 \cdot 0.7\hspace{0.15cm}\underline{= 0.49},$$
- $$p_{\rm B} = \rm Pr(XY) = 0.7 \cdot 0.2\hspace{0.15cm}\underline{= 0.14},$$
- $$p_{\rm C} = \rm Pr(XZ) = 0.7 \cdot 0.1\hspace{0.15cm}\underline{= 0.07},$$
- $$p_{\rm D} = \rm Pr(YX) = 0.2 \cdot 0.7 = 0.14,$$
- $$p_{\rm E} = \rm Pr(YY) = 0.2 \cdot 0.2 = 0.04,$$
- $$p_{\rm F} = \rm Pr(YZ) = 0.2 \cdot 0.1 = 0.02,$$
- $$p_{\rm G} = \rm Pr(ZX) = 0.1 \cdot 0.7 = 0.07,$$
- $$p_{\rm H} = \rm Pr(ZY) = 0.1 \cdot 0.2 = 0.02,$$
- $$p_{\rm I} = \rm Pr(ZZ) = 0.1 \cdot 0.1 = 0.01.$$
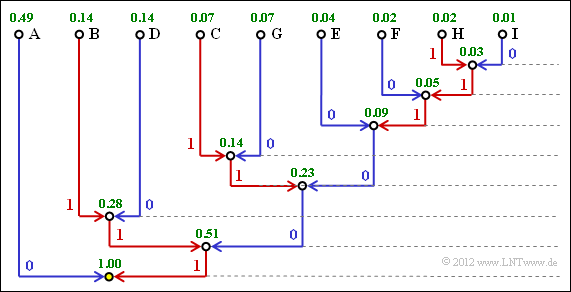
(3) The graph shows the Huffman tree for the application with $k = 2$. Thus we obtain
- for the individual two-tuples the following binary codings:
- $\rm XX = A$ → 0, $\rm XY = B$ → 111, $\rm XZ = C$ → 1011,
- $\rm YX = D$ → 110, $\rm YY = E$ → 1000, $\rm YZ = F$ → 10010,
- $\rm ZX = G$ → 1010, $\rm ZY = H$ → 100111, $\rm ZZ =I$ → 100110;
- for the average code word length:
- $$L_{\rm M}\hspace{0.01cm}' =0.49 \cdot 1 + (0.14 + 0.14) \cdot 3 + (0.07 + 0.04 + 0.07) \cdot 4 + 0.02 \cdot 5 + (0.02 + 0.01) \cdot 6 = 2.33\,\,{\rm bit/two tuples}$$
- $$\Rightarrow\hspace{0.3cm}L_{\rm M} = {L_{\rm M}\hspace{0.01cm}'}/{2}\hspace{0.15cm}\underline{ = 1.165\,\,{\rm bit/source\hspace{0.12cm}symbol}}\hspace{0.05cm}.$$
(4) Statement 1 is correct, even if $L_{\rm M}$ decreases very slowly as $k$ increases.
- The last statement is false because $L_{\rm M}$ cannot be smaller than $H = 1.157$ bit/source symbol even for $k → ∞$ .
- But the second statement is not necessarily correct either: Since $L_{\rm M} > H$ still applies with $k = 2$ , $k = 3$ can lead to a further improvement.