Exercise 2.9: Symmetrical Distortions

• Return to book

Transmitter and receiver spectrum in the equivalent low-pass region

The source signal made up of two components

$$q(t) = A_1 \cdot \cos(2 \pi f_1 t ) + A_2 \cdot \cos(2 \pi f_2 t )$$

is amplitude modulated and transmitted through a linearly distorting transmission channel. 

• The carrier frequency is  $f_{\rm T}$  and the added DC component  $A_{\rm T}$. 
• Thus,  a  "double-sideband amplitude moduluation"  $\rm (DSB–AM)$ with carrier"  is present.

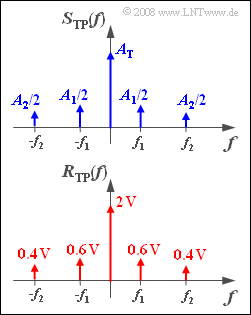
The upper graph shows the spectrum  $S_{\rm TP}(f)$  of the equivalent low-pass signal in schematic form.  This means that the lengths of the Dirac delta lines drawn do not correspond to the actual values of  $A_{\rm T}$,  $A_1/2$  and  $A_2/2$.

The spectral function  $R(f)$  of the received signal was measured.  In the lower graph we can observe the equivalent low-pass spectrum  $R_{\rm TP}(f)$ calculated from this.

The channel frequency response is characterized with sufficient accuracy with a few auxiliary values:

$$ H_{\rm K}(f = f_{\rm T}) = 0.5,$$

$$H_{\rm K}(f = f_{\rm T} \pm f_1) = 0.4,$$

$$ H_{\rm K}(f = f_{\rm T} \pm f_2) = 0.2 \hspace{0.05cm}.$$

Hints:

• This exercise belongs to the chapter  Envelope Demodulation.
• Particular reference is made to the section  Description using the equivalent low-pass signal.

Questions

1

Give the amplitudes of the carrier and source signal.

$A_{\rm T} \ = \hspace{0.17cm} $ $\ \rm V$

$A_1 \ = \ $ $\ \rm V$

$A_2 \ = \ $ $\ \rm V$

2

Which kind of distortion would the application of an envelope demodulator in an ideal channel   ⇒   $H_{\rm K}(f) = 1$  lead to?

	No distortion.
	Linear distortions.
	Nonlinear distortions.

3

Calculate the equivalent low-pass signal and answer the following questions. Is it true that...

	$r_{\rm TP}(t)$  is always real,
	$r_{\rm TP}(t)$  is always greater than or equal to zero,
	the phase function  $ϕ(t)$  can take on the values  $0^\circ$  and  $180^\circ$ .

4

Which kind of distortion does the envelope demodulator in the observed transmission channel lead to?

	No distortion.
	Linear distortions.
	Nonlinear distortions.

Solution

Solution

(1)  On the basis of the graphs on the exercise page,  the following statements can be made:

$${A_{\rm T}} \cdot 0.5 = 2 \,{\rm V}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}A_{\rm T} \hspace{0.15cm}\underline {= 4 \,{\rm V}},$$

$${A_{\rm 1}}/{2} \cdot 0.4 = 0.6\,{\rm V}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}A_{\rm 1} \hspace{0.15cm}\underline {= 3 \,{\rm V}},$$

$${A_{\rm 2}}/{2} \cdot 0.2 = 0.4\,{\rm V}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}A_{\rm 2} \hspace{0.15cm}\underline {= 4 \,{\rm V}}\hspace{0.05cm}.$$

(2)  Answer 3  is correct:

• The resulting modulation depth is   $m = (A_1 + A_2)/A_T = 1.75 >1$.
• This leads to strong nonlinear distortion when using an envelope demodulator.
• A distortion factor cannot be specified because the source signal contains two frequency components.

(3)  Answers 1 and 2 are correct:

• The Fourier retransform of   $R_{\rm TP}(f)$  gives us the result:

$$ r_{\rm TP}(t) = 2 \,{\rm V} + 1.2 \,{\rm V} \cdot \cos(2 \pi f_1 t ) + 0.8 \,{\rm V} \cdot \cos(2 \pi f_2 t )\hspace{0.05cm}.$$

• This function is always real and non-negative.
• Thus,  $ϕ(t) = 0$  holds simultaneously,  whereas  $ϕ(t) = 180^\circ$  is not possible.

(4)  A comparison of the two signals

$$q(t) = 3 \,{\rm V} \cdot \cos(2 \pi f_1 t ) + 4 \,{\rm V} \cdot \cos(2 \pi f_2 t ),$$

$$ v(t) = 0.4 \cdot 3 \,{\rm V} \cdot \cos(2 \pi f_1 t ) + 0.2 \cdot 4 \,{\rm V} \cdot \cos(2 \pi f_2 t )$$

shows,  that linear (attenuation) distortions now arise   ⇒   Answer 2.

• Here, the channel  $H_{\rm K}(f)$  has the positive effect,  that instead of irreversible nonlinear distortions,  only linear distortions arise,  and these can be eliminated by a downstream filter.
• This is due to the fact that the higher attenuation of the source signal  $q(t)$  compared to the carrier signal  $z(t)$  lowers the modulation depth from   $m = 1.75$  to 

$$m = (0.4 · 3 \ \rm V + 0.2 · 4 \ \rm V)/(0.5 · 4 \ \rm V) = 1.$$