Difference between revisions of "Aufgaben:Exercise 3.1Z: Hilbert Transform"
m (Markus verschob die Seite Zusatzaufgaben:3.1 Hilbert-Transformierte nach 3.1Z Hilbert-Transformierte, ohne dabei eine Weiterleitung anzulegen) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID1756__LZI_Z_3_1.png|right|]] | + | [[File:P_ID1756__LZI_Z_3_1.png|right|Betrachtete Impulsantworten]] |
| − | + | Der Zusammenhang zwischen dem Real– und dem Imginärteil der Übertragungsfunktion realisierbarer kausaler Systeme wird durch die Hilbert–Transformation beschrieben. Hierbei gilt: | |
| − | + | $${\rm Im} \left\{ H(f) \right \} = - \frac{1}{\pi }\int\limits_{-\infty}^{ | |
+\infty} | +\infty} | ||
{ \frac{{\rm Re} \left\{ H(\nu) \right \}}{f - \nu}}\hspace{0.1cm}{\rm | { \frac{{\rm Re} \left\{ H(\nu) \right \}}{f - \nu}}\hspace{0.1cm}{\rm | ||
d}\nu \hspace{0.05cm},$$ | d}\nu \hspace{0.05cm},$$ | ||
| − | + | $${\rm Re} \left\{ H(f) \right \} = \frac{1}{\pi }\int\limits_{-\infty}^{ | |
+\infty} | +\infty} | ||
{ \frac{{\rm Im} \left\{ H(\nu) \right \}}{f - \nu}}\hspace{0.1cm}{\rm | { \frac{{\rm Im} \left\{ H(\nu) \right \}}{f - \nu}}\hspace{0.1cm}{\rm | ||
d}\nu \hspace{0.05cm}.$$ | d}\nu \hspace{0.05cm}.$$ | ||
| − | + | Als gemeinsames Kurzzeichen verwendet man für diese beiden Integraltransformationen: | |
| − | + | $${\rm Im} \left\{ H(f) \right \} \quad | |
\bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad | \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad | ||
{\rm Re} \left\{ H(f) \right \}\hspace{0.05cm}.$$ | {\rm Re} \left\{ H(f) \right \}\hspace{0.05cm}.$$ | ||
| − | + | Da sich die Hin– und die Rücktransformation lediglich durch das Vorzeichen unterscheiden, genügt eine Gleichung. Dabei gilt: | |
| − | + | * Zur Berechnung des durch den Pfeil markierten Operanden wird das positive Vorzeichen verwendet. | |
| − | + | * Dagegen ist zur Berechnung des durch den Kreis markierten Operanden das Minuszeichen zu berücksichtigen. | |
| − | + | Die Hilbert–Transformation gilt viel allgemeiner als nur für den hier beschriebenen Anwendungsfall. Zum Beispiel wird sie auch verwendet, um zu einem reellen Bandpass–Signal das dazugehörige (komplexe) analytische Signal zu ermitteln. | |
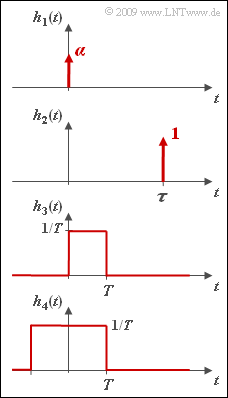
| − | + | Bei dieser Aufgabe soll zu den in der Grafik gegebenen kausalen Impulsantworten $h(t)$ die zugehörigen Frequenzgänge $H(f)$ entsprechend der Fourierrücktransformation ermittelt werden. Zerlegt man $H(f)$ jeweils in Real– und Imaginärteil, so können daraus Hilbert–Korrespondenzen abgeleitet werden. | |
| − | : | + | ''Hinweise:'' |
| + | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Folgerungen_aus_dem_Zuordnungssatz|Folgerungen aus dem Zuordnungssatz]]. | ||
| + | *Bezug genommen wird insbesondere auf die Therieseite [[Lineare_zeitinvariante_Systeme/Folgerungen_aus_dem_Zuordnungssatz#Hilbert.E2.80.93Transformation|Hilbert-Transformation]]. | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| Line 35: | Line 38: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Ermitteln Sie ausgehend von | + | {Ermitteln Sie ausgehend von $h_1(t) = \alpha \cdot \delta(t)$ die Hilbert–Transformierte einer Konstanten $\alpha$. Welche Aussagen treffen zu? |
|type="[]"} | |type="[]"} | ||
| − | - Die Hilbert–Transformierte einer Konstanten | + | - Die Hilbert–Transformierte einer Konstanten $\alpha$ ist ebenfalls $\alpha$. |
| − | + Die Hilbert–Transformierte einer Konstanten | + | + Die Hilbert–Transformierte einer Konstanten $\alpha$ ist $0$. |
| − | - Die Hilbert–Transformierte einer Konstanten | + | - Die Hilbert–Transformierte einer Konstanten $\alpha$ verläuft sinusförmig. |
| − | {Ermitteln Sie ausgehend von | + | {Ermitteln Sie ausgehend von $h_2(t) = \delta(t- \tau)$ die Hilbert–Transformierte einer Cosinusfunktion. Welche Aussagen treffen zu? |
|type="[]"} | |type="[]"} | ||
- Die Hilbert–Transformierte von einem Cosinus ist eine Konstante. | - Die Hilbert–Transformierte von einem Cosinus ist eine Konstante. | ||
| − | - Die Hilbert–Transformierte einer Cosinusfunktion ist 0. | + | - Die Hilbert–Transformierte einer Cosinusfunktion ist $0$. |
+ Die Hilbert–Transformierte von einem Cosinus verläuft sinusförmig. | + Die Hilbert–Transformierte von einem Cosinus verläuft sinusförmig. | ||
| − | {Ermitteln Sie ausgehend vom rechteckförmigen | + | {Ermitteln Sie ausgehend vom rechteckförmigen $h_3(t)$ die Hilbert–Transformierte der Funktion ${\rm si}(2 \pi;fT) = {\rm sin}(2 \pi;fT)/(2 \pi;fT)$ Welche Aussagen treffen zu? |
|type="[]"} | |type="[]"} | ||
| − | + Die Hilbert Transformierte lautet sin | + | + Die Hilbert Transformierte lautet ${\rm sin}^2(\pi;fT)/(\pi;fT)$. |
| − | + Die Hilbert Transformierte lautet sin( | + | + Die Hilbert Transformierte lautet $ = {\rm sin}( \pi;fT) \cdot {\rm si}( \pi;fT)$. |
| − | {Lässt sich aus der Impulsantwort | + | {Lässt sich aus der Impulsantwort $h_4(t)$ eine Hilbert–Korrespondenz ableiten? |
|type="[]"} | |type="[]"} | ||
- Ja. | - Ja. | ||
Revision as of 17:04, 7 February 2017
Der Zusammenhang zwischen dem Real– und dem Imginärteil der Übertragungsfunktion realisierbarer kausaler Systeme wird durch die Hilbert–Transformation beschrieben. Hierbei gilt: $${\rm Im} \left\{ H(f) \right \} = - \frac{1}{\pi }\int\limits_{-\infty}^{ +\infty} { \frac{{\rm Re} \left\{ H(\nu) \right \}}{f - \nu}}\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm},$$ $${\rm Re} \left\{ H(f) \right \} = \frac{1}{\pi }\int\limits_{-\infty}^{ +\infty} { \frac{{\rm Im} \left\{ H(\nu) \right \}}{f - \nu}}\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$
Als gemeinsames Kurzzeichen verwendet man für diese beiden Integraltransformationen: $${\rm Im} \left\{ H(f) \right \} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad {\rm Re} \left\{ H(f) \right \}\hspace{0.05cm}.$$
Da sich die Hin– und die Rücktransformation lediglich durch das Vorzeichen unterscheiden, genügt eine Gleichung. Dabei gilt:
- Zur Berechnung des durch den Pfeil markierten Operanden wird das positive Vorzeichen verwendet.
- Dagegen ist zur Berechnung des durch den Kreis markierten Operanden das Minuszeichen zu berücksichtigen.
Die Hilbert–Transformation gilt viel allgemeiner als nur für den hier beschriebenen Anwendungsfall. Zum Beispiel wird sie auch verwendet, um zu einem reellen Bandpass–Signal das dazugehörige (komplexe) analytische Signal zu ermitteln.
Bei dieser Aufgabe soll zu den in der Grafik gegebenen kausalen Impulsantworten $h(t)$ die zugehörigen Frequenzgänge $H(f)$ entsprechend der Fourierrücktransformation ermittelt werden. Zerlegt man $H(f)$ jeweils in Real– und Imaginärteil, so können daraus Hilbert–Korrespondenzen abgeleitet werden.
Hinweise:
- Die Aufgabe gehört zum Kapitel Folgerungen aus dem Zuordnungssatz.
- Bezug genommen wird insbesondere auf die Therieseite Hilbert-Transformation.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
- 1. Die Fourier–Transformierte von h1(t) = α · δ(t) lautet:
- $$H_1(f) = \alpha \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Re} \left\{ H_1(f) \right \} = \alpha , \hspace{0.2cm}{\rm Im} \left\{ H_1(f) \right \} = 0\hspace{0.05cm}.$$
- Richtig ist somit der zweite Lösungsvorschlag.
- 2. Mit dem Verschiebungssatz und dem Satz von Euler erhält man für die Impulsantwort h2(t) den Frequenzgang:
- $$H_2(f) ={\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f \tau} = \cos (2\pi f \tau) - {\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \sin (2\pi f \tau)\hspace{0.05cm}.$$
- Daraus ergibt sich die Hilbert–Korrespondenz
- $$\cos (2\pi f \tau) \hspace{0.3cm} \leftarrow\hspace{-0.05cm}\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.3cm} -\sin (2\pi f \tau)\hspace{0.7cm}{\rm oder}\hspace{0.7cm} \cos (2\pi f \tau) \hspace{0.3cm} \bullet\hspace{-0.05cm}\!\!-\!\!\!-\!\!\!-\!-\!\hspace{-0.1cm}\rightarrow\hspace{0.3cm} \sin (2\pi f \tau) \hspace{0.05cm}.$$
- entsprechend dem letzten Lösungsvorschlag.
- 3. Für die rechteckförmige Impulsantwort h3(t) mit der Breite T und der Höhe 1/T erhält man die Spektralfunktion entsprechend dem ersten Fourierintegral:
- $$H_3(f) = \int\limits_{-\infty}^{ +\infty} { h_3(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f t}}\hspace{0.1cm}{\rm d}t \hspace{0.05cm} = \frac{1}{T} \cdot \int\limits_{0}^{ T} { {\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f t}}\hspace{0.1cm}{\rm d}t = \\ = \left [\frac{1}{-{\rm j}\cdot 2\pi f T} \cdot {\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f\hspace{0.05cm} t} \right ]_{0}^{T} = \frac{1-{\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f\hspace{0.05cm} T}}{{\rm j}\cdot 2\pi f T} \hspace{0.05cm}.$$
- Mit dem Eulerschen Satz kann hierfür auch geschrieben werden:
- $$H_3(f) = \frac{1-\cos (2\pi f T) + {\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \sin (2\pi f T)}{{\rm j}\cdot 2\pi f T} =\\ = \frac{\sin (2\pi f T)}{ 2\pi f T} - {\rm j}\cdot \frac{1 - \cos (2\pi f T)}{ 2\pi f T}\hspace{0.05cm}.$$
- Weiter gilt mit der Umformung 1 – cos(α) = 2 · sin2(α/2):
- $${\rm Re} \left\{ H_3(f) \right \} = {\rm si} (2\pi f T)\hspace{0.2cm}{\rm mit}\hspace{0.2cm}{\rm si}(x)= {\rm sin}(x)/x \hspace{0.05cm},\\ {\rm Im} \left\{ H_3(f) \right \} = -\frac{\sin^2 (\pi f T)}{ \pi f T}= - {\rm si} (\pi f T) \cdot {\rm sin} (\pi f T) \hspace{0.05cm}.$$
- Daraus folgt, dass beide Lösungsalternativen richtig sind.
- 4. Nein. Die Impulsantwort h4(t) ist nicht kausal, so dass aus dem dazugehörigen Fourier–Spektrum H4(f) keine Hilbert–Korrespondenz abgeleitet werden kann.