Difference between revisions of "Aufgaben:Exercise 3.6: PM or FM? Or AM?"
From LNTwww
m (→Solution) |
|||
| (18 intermediate revisions by 4 users not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
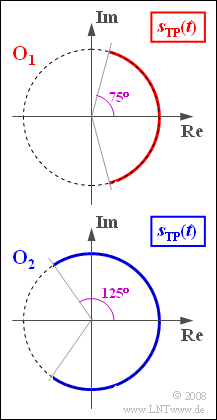
| − | [[File:P_ID1102__Mod_A_3_6.png|right|]] | + | [[File:P_ID1102__Mod_A_3_6.png|right|frame|Two different locus curves for angle modulation]] |
| − | + | To analyze a modulator, apply the signal | |
| − | $$q(t) = A_{\rm N} \cdot \cos(2 \pi \cdot f_{\rm N} \cdot t + \phi_{\rm N})$$ | + | :$$q(t) = A_{\rm N} \cdot \cos(2 \pi \cdot f_{\rm N} \cdot t + \phi_{\rm N})$$ |
| − | + | to its input, where the signal amplitude is always $A_{\rm N} = 2\ \rm V$ . | |
| + | *Using the signal frequency $f_{\rm N} = f_1 = 5 \ \rm kHz$ the locus $\rm O_1$ is determined. | ||
| + | *If one uses the message frequency $f_{\rm N} = f_2$, then the $\rm O_2$ locus is established. | ||
| − | |||
| − | |||
| − | |||
| + | In your solutions, note that for angle modulation – the umbrella term for phase and frequency modulation – the following relationship holds between the modulation index $η$ and the modulator constant $K_{\rm WM}$: | ||
| + | :$$\eta = \left\{ \begin{array}{c} K_{\rm WM} \cdot A_{\rm N} \\ {K_{\rm WM} \cdot A_{\rm N}}/({2 \pi \cdot f_{\rm N})} \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{bei}} \\ {\rm{bei}} \\ \end{array}\begin{array}{*{20}c} {\rm PM} \hspace{0.05cm}, \\ {\rm FM}. \hspace{0.05cm} \\ \end{array}$$ | ||
| − | === | + | |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Hints:'' | ||
| + | *This exercise belongs to the chapter [[Modulation_Methods/Frequency_Modulation_(FM)|Frequency Modulation]]. | ||
| + | *Reference is also made to the chapter [[Modulation_Methods/Phase_Modulation_(PM)|Phase Modulation]]. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which modulator do we have here? |
| − | |type=" | + | |type="()"} |
| − | - | + | - AM modulator. |
| − | - | + | - PM modulator. |
| − | + | + | + FM modulator. |
| − | { | + | {What is the modulation index when the message frequency is $f_{\rm N} = f_1 = 5 \ \rm kHz$? |
|type="{}"} | |type="{}"} | ||
| − | $η_1$ | + | $η_1 \ = \ $ { 1.3 3% } |
| − | { | + | {What is the value of the modulator constant? ''Hint:'' the "unit" stands for $\rm V^{-1}$ (for PM) or $\rm (Vs)^{-1}$ (for FM). |
|type="{}"} | |type="{}"} | ||
| − | $K_{WM}$ | + | $K_{\rm WM} \ = \ $ { 2.04 3% } $\ \cdot 10^4 $ "unit" |
| − | { | + | {What is the angle $ϕ_0$ (with respect to the real axis) of the locus curve $\rm O_1$ when $ϕ_{\rm N} = 30^\circ$ at time $t = 0$ ? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $ϕ_0 \ = \ $ { 37.5 3% } $\ \rm degrees$ |
| − | { | + | {What message frequency $f_{\rm N} = f_2$ was used to determine the locus $\rm O_2$ ? |
|type="{}"} | |type="{}"} | ||
| − | $f_2$ | + | $f_2 \ = \ ${ 3 3% } $\ \rm kHz$ |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' <u>Answer 3</u> is correct: |
| + | *Since the locus curve describes an arc, we have an angle modulator (PM or FM) with modulation index $η$. | ||
| + | *But since $η$ here clearly depends on the message frequency $f_{\rm N}$ , we can rule out phase modulation. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' The modulation index can be read off the graph. It is $η_1 = 75^\circ/180^\circ · π\hspace{0.15cm}\underline { ≈ 1.3}$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' For frequency modulation, it holds that: | ||
| + | :$$ K_{\rm WM} = K_{\rm FM} = \frac{ 2 \pi \cdot f_{\rm N} \cdot \eta}{A_{\rm N}} = \frac{ 2 \pi \cdot 5 \cdot 10^3 \,\,{\rm Hz}\cdot 1.3}{2\,{\rm V}} \hspace{0.15cm}\underline {\approx 2.04 \cdot 10^4 \hspace{0.1cm}{\rm V^{-1}}{\rm s^{-1}}}\hspace{0.05cm}.$$ | ||
| − | |||
| + | '''(4)''' The frequency modulator can be realized as a phase modulator if the source signal is integrated beforehand. This is: | ||
| + | :$$q_{\rm I}(t) = \int q(t)\hspace{0.15cm}{\rm d}t = A_{\rm N} \cdot\int \cos(\omega_{\rm N} \cdot t + \phi_{\rm N})\hspace{0.15cm}{\rm d}t =\frac{A_{\rm N}}{\omega_{\rm N}} \cdot \sin(\omega_{\rm N} \cdot t + \phi_{\rm N}) = \frac{A_{\rm N}}{\omega_{\rm N}} \cdot \cos(\omega_{\rm N} \cdot t + \phi_{\rm N} - 90^\circ)\hspace{0.05cm}.$$ | ||
| + | *Thus, for the equivalent low-pass signal with $ϕ_{\rm N} = 30^\circ$: | ||
| + | :$$s_{\rm TP}(t) = {\rm e}^{{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\eta \hspace{0.03cm}\cdot \hspace{0.05cm}\cos(\omega_{\rm N} \hspace{0.03cm}\cdot \hspace{0.03cm}t \hspace{0.03cm} - \hspace{0.03cm}60^\circ)}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}s_{\rm TP}(t = 0) = {\rm e}^{{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\eta \hspace{0.03cm}\cdot \hspace{0.05cm}\cos(\hspace{0.03cm}60^\circ)} = {\rm e}^{{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\eta /2}\hspace{0.05cm}.$$ | ||
| + | *Thus, the zero phase angle is equal to $η/2$ corresponding to $ϕ_0\hspace{0.15cm}\underline {\approx 37.5^\circ}$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''5 | + | '''(5)''' From the definition of modulation index in frequency modulation, it follows that: |
| − | $$\eta_1 = \frac{K_{\rm WM} \cdot A_{\rm N}}{2 \pi \cdot f_{\rm 1}}\hspace{0.05cm},\hspace{0.3cm} \eta_2 = \frac{K_{\rm WM} \cdot A_{\rm N}}{2 \pi \cdot f_{\rm 2}} | + | :$$\eta_1 = \frac{K_{\rm WM} \cdot A_{\rm N}}{2 \pi \cdot f_{\rm 1}}\hspace{0.05cm},\hspace{0.3cm} \eta_2 = \frac{K_{\rm WM} \cdot A_{\rm N}}{2 \pi \cdot f_{\rm 2}} \hspace{0.3cm} |
| − | + | \Rightarrow \hspace{0.3cm}\frac{\eta_1}{\eta_2} = \frac{f_2}{f_1}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} f_2 = \frac{\eta_1}{\eta_2} \cdot f_1 = \frac{75^\circ}{125^\circ} \cdot 5\,{\rm kHz} \hspace{0.15cm}\underline {= 3\,{\rm kHz}}\hspace{0.05cm}.$$ | |
| Line 71: | Line 93: | ||
| − | [[Category: | + | [[Category:Modulation Methods: Exercises|^3.2 Frequency Modulation^]] |
Latest revision as of 15:13, 17 March 2022
To analyze a modulator, apply the signal
- $$q(t) = A_{\rm N} \cdot \cos(2 \pi \cdot f_{\rm N} \cdot t + \phi_{\rm N})$$
to its input, where the signal amplitude is always $A_{\rm N} = 2\ \rm V$ .
- Using the signal frequency $f_{\rm N} = f_1 = 5 \ \rm kHz$ the locus $\rm O_1$ is determined.
- If one uses the message frequency $f_{\rm N} = f_2$, then the $\rm O_2$ locus is established.
In your solutions, note that for angle modulation – the umbrella term for phase and frequency modulation – the following relationship holds between the modulation index $η$ and the modulator constant $K_{\rm WM}$:
- $$\eta = \left\{ \begin{array}{c} K_{\rm WM} \cdot A_{\rm N} \\ {K_{\rm WM} \cdot A_{\rm N}}/({2 \pi \cdot f_{\rm N})} \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{bei}} \\ {\rm{bei}} \\ \end{array}\begin{array}{*{20}c} {\rm PM} \hspace{0.05cm}, \\ {\rm FM}. \hspace{0.05cm} \\ \end{array}$$
Hints:
- This exercise belongs to the chapter Frequency Modulation.
- Reference is also made to the chapter Phase Modulation.
Questions
Solution
(1) Answer 3 is correct:
- Since the locus curve describes an arc, we have an angle modulator (PM or FM) with modulation index $η$.
- But since $η$ here clearly depends on the message frequency $f_{\rm N}$ , we can rule out phase modulation.
(2) The modulation index can be read off the graph. It is $η_1 = 75^\circ/180^\circ · π\hspace{0.15cm}\underline { ≈ 1.3}$.
(3) For frequency modulation, it holds that:
- $$ K_{\rm WM} = K_{\rm FM} = \frac{ 2 \pi \cdot f_{\rm N} \cdot \eta}{A_{\rm N}} = \frac{ 2 \pi \cdot 5 \cdot 10^3 \,\,{\rm Hz}\cdot 1.3}{2\,{\rm V}} \hspace{0.15cm}\underline {\approx 2.04 \cdot 10^4 \hspace{0.1cm}{\rm V^{-1}}{\rm s^{-1}}}\hspace{0.05cm}.$$
(4) The frequency modulator can be realized as a phase modulator if the source signal is integrated beforehand. This is:
- $$q_{\rm I}(t) = \int q(t)\hspace{0.15cm}{\rm d}t = A_{\rm N} \cdot\int \cos(\omega_{\rm N} \cdot t + \phi_{\rm N})\hspace{0.15cm}{\rm d}t =\frac{A_{\rm N}}{\omega_{\rm N}} \cdot \sin(\omega_{\rm N} \cdot t + \phi_{\rm N}) = \frac{A_{\rm N}}{\omega_{\rm N}} \cdot \cos(\omega_{\rm N} \cdot t + \phi_{\rm N} - 90^\circ)\hspace{0.05cm}.$$
- Thus, for the equivalent low-pass signal with $ϕ_{\rm N} = 30^\circ$:
- $$s_{\rm TP}(t) = {\rm e}^{{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\eta \hspace{0.03cm}\cdot \hspace{0.05cm}\cos(\omega_{\rm N} \hspace{0.03cm}\cdot \hspace{0.03cm}t \hspace{0.03cm} - \hspace{0.03cm}60^\circ)}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}s_{\rm TP}(t = 0) = {\rm e}^{{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\eta \hspace{0.03cm}\cdot \hspace{0.05cm}\cos(\hspace{0.03cm}60^\circ)} = {\rm e}^{{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\eta /2}\hspace{0.05cm}.$$
- Thus, the zero phase angle is equal to $η/2$ corresponding to $ϕ_0\hspace{0.15cm}\underline {\approx 37.5^\circ}$.
(5) From the definition of modulation index in frequency modulation, it follows that:
- $$\eta_1 = \frac{K_{\rm WM} \cdot A_{\rm N}}{2 \pi \cdot f_{\rm 1}}\hspace{0.05cm},\hspace{0.3cm} \eta_2 = \frac{K_{\rm WM} \cdot A_{\rm N}}{2 \pi \cdot f_{\rm 2}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\frac{\eta_1}{\eta_2} = \frac{f_2}{f_1}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} f_2 = \frac{\eta_1}{\eta_2} \cdot f_1 = \frac{75^\circ}{125^\circ} \cdot 5\,{\rm kHz} \hspace{0.15cm}\underline {= 3\,{\rm kHz}}\hspace{0.05cm}.$$