Difference between revisions of "Aufgaben:Exercise 4.7: Spectra of ASK and BPSK"
m (Text replacement - "Category:Aufgaben zu Modulationsverfahren" to "Category:Modulation Methods: Exercises") |
|||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
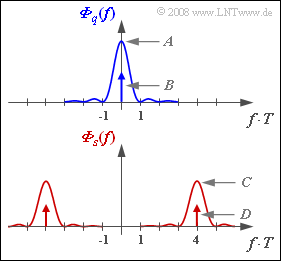
| − | [[File:P_ID1701__Mod_A_4_6.png|right|frame|Leistungsdichtespektren von $q(t)$ und $s(t)$ – gültig für ASK und BPSK]] | + | [[File:P_ID1701__Mod_A_4_6.png|right|frame|Leistungsdichtespektren von $q(t)$ und $s(t)$ – gültig für ASK und BPSK]] |
| − | Die Sendesignale von ASK (''Amplitude Shift Keying'') und BPSK (''Binary Phase Shift Keying'') können beide in der Form | + | Die Sendesignale von ASK (''Amplitude Shift Keying'') und BPSK (''Binary Phase Shift Keying'') können beide in der Form |
:$$s(t) = q(t) · z(t)$$ | :$$s(t) = q(t) · z(t)$$ | ||
| − | dargestellt werden, wobei $z(t)$ eine harmonische Schwingung mit der Frequenz $f_{\rm T}$ und der Amplitude $1$ darstellt. Die Trägerphase $ϕ_{\rm T}$ ist für die hier betrachteten Leistungsdichtespektren nicht von Bedeutung. | + | dargestellt werden, wobei $z(t)$ eine harmonische Schwingung mit der Frequenz $f_{\rm T}$ und der Amplitude $1$ darstellt. Die Trägerphase $ϕ_{\rm T}$ ist für die hier betrachteten Leistungsdichtespektren nicht von Bedeutung. |
*Die Quelle ist jeweils redundanzfrei, was bedeutet, dass die beiden möglichen Symbole $±1$ gleichwahrscheinlich sind und die Symbole statistisch voneinander unabhängig. | *Die Quelle ist jeweils redundanzfrei, was bedeutet, dass die beiden möglichen Symbole $±1$ gleichwahrscheinlich sind und die Symbole statistisch voneinander unabhängig. | ||
| Line 14: | Line 14: | ||
| − | In der Grafik sind die Leistungsdichtespektren ${\it Φ}_q(f)$ und ${\it Φ}_s(f)$ von Quellensignal und Sendesignal angegeben, die sich bei einem NRZ–Rechteckimpuls $g_q(t)$ mit der Amplitude $s_0 = 2 \ \rm V$ und der Dauer $T = 1 \ \rm µ s$ ergeben. Damit lautet die Spektralfunktion: | + | In der Grafik sind die Leistungsdichtespektren ${\it Φ}_q(f)$ und ${\it Φ}_s(f)$ von Quellensignal und Sendesignal angegeben, die sich bei einem NRZ–Rechteckimpuls $g_q(t)$ mit der Amplitude $s_0 = 2 \ \rm V$ und der Dauer $T = 1 \ \rm µ s$ ergeben. Damit lautet die Spektralfunktion: |
:$$G_q(f) = s_0 \cdot T \cdot {\rm si}(\pi f T)\hspace{0.05cm}.$$ | :$$G_q(f) = s_0 \cdot T \cdot {\rm si}(\pi f T)\hspace{0.05cm}.$$ | ||
| − | Zu bestimmen sind die Konstanten $A$, $B$, $C$ und $D$ für die Modulationsverfahren | + | Zu bestimmen sind die Konstanten $A$, $B$, $C$ und $D$ für die Modulationsverfahren $\rm ASK$ und $\rm BPSK$. |
| + | |||
| + | |||
| + | |||
| Line 24: | Line 27: | ||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[ | + | *Die Aufgabe gehört zum Kapitel [[Modulation_Methods/Lineare_digitale_Modulation|Lineare digitale Modulation]]. |
| − | *Bezug genommen wird aber auch auf das Kapitel [[ | + | *Bezug genommen wird aber auch auf das Kapitel [[Digital_Signal_Transmission/Grundlagen_der_codierten_Übertragung|Grundlagen der codierten Übertragung]] im Buch „Digitalsignalübertragung”. |
| − | *Die Leistungen sind in $\rm V^2$ anzugeben; sie beziehen sich somit auf den Bezugswiderstand $R = 1 \ \rm \Omega$. | + | *Die Leistungen sind in $\rm V^2$ anzugeben; sie beziehen sich somit auf den Bezugswiderstand $R = 1 \ \rm \Omega$. |
| Line 65: | Line 68: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Der Gleichanteil des unipolaren redundanzfreien Quellensignals beträgt $m_q = s_0/2$. Das Diracgewicht ist somit $B = m_q^2 = s_0^2/4\hspace{0.15cm}\underline{ = 1 \ \rm V^2}$. | + | '''(1)''' Der Gleichanteil des unipolaren redundanzfreien Quellensignals beträgt $m_q = s_0/2$. Das Diracgewicht ist somit $B = m_q^2 = s_0^2/4\hspace{0.15cm}\underline{ = 1 \ \rm V^2}$. |
| − | Ohne diesen Gleichanteil ergäbe sich das stochastische Rechtecksignal $q(t) | + | *Ohne diesen Gleichanteil ergäbe sich das stochastische Rechtecksignal $q(t) - m_q ∈ \{+s_0/2, -s_0/2\}$. |
| + | *Dieses gleichsignalfreie Signal besitzt den kontinuierlichen LDS–Anteil $(s_0/2)^2 · T · {\rm si}^2(πfT)$. | ||
| + | *Hieraus lässt sich der gesuchte Wert bei der Frequenz $f = 0$ ermitteln: | ||
:$$A = \frac {s_0^2 \cdot T }{4} = \frac {(2\,{\rm V})^2 \cdot | :$$A = \frac {s_0^2 \cdot T }{4} = \frac {(2\,{\rm V})^2 \cdot | ||
10^{-6} \,{\rm s}}{4}\hspace{0.15cm}\underline {= 10^{-6} \,{\rm V^{2}/Hz}}.$$ | 10^{-6} \,{\rm s}}{4}\hspace{0.15cm}\underline {= 10^{-6} \,{\rm V^{2}/Hz}}.$$ | ||
| − | '''(2)''' Das Spektrum $Z(f)$ eines Cosinussignals $z(t)$ besteht aus zwei Diracfunktionen bei $\pm f_{\rm T}$, jeweils mit dem Gewicht $1/2$. | + | |
| − | *Das Leistungsdichtespektrum ${\it Φ}_z(f)$ besteht ebenfalls aus den beiden Diracfunktionen, nun aber mit jeweiligem Gewicht $1/4$. | + | |
| − | *Die Faltung ${\it Φ}_q(f) ∗ {\it Φ}_z(f)$ ergibt das Leistungsdichtespektrum ${\it Φ}_s(f)$ des Sendesignals. Daraus folgt: | + | '''(2)''' Das Spektrum $Z(f)$ eines Cosinussignals $z(t)$ besteht aus zwei Diracfunktionen bei $\pm f_{\rm T}$, jeweils mit dem Gewicht $1/2$. |
| + | *Das Leistungsdichtespektrum ${\it Φ}_z(f)$ besteht ebenfalls aus den beiden Diracfunktionen, nun aber mit jeweiligem Gewicht $1/4$. | ||
| + | *Die Faltung ${\it Φ}_q(f) ∗ {\it Φ}_z(f)$ ergibt das Leistungsdichtespektrum ${\it Φ}_s(f)$ des Sendesignals. Daraus folgt: | ||
:$$C = {A}/{4} \hspace{0.15cm}\underline { = 0.25 \cdot 10^{-6} \,{\rm | :$$C = {A}/{4} \hspace{0.15cm}\underline { = 0.25 \cdot 10^{-6} \,{\rm | ||
V^{2}/Hz}},\hspace{0.2cm}D = {B}/{4}\hspace{0.15cm}\underline { = 0.25 \,{\rm V^{2}}}.$$ | V^{2}/Hz}},\hspace{0.2cm}D = {B}/{4}\hspace{0.15cm}\underline { = 0.25 \,{\rm V^{2}}}.$$ | ||
| − | ''Anmerkung:'' Die Leistung pro Bit ergibt sich als das Integral über ${\it Φ}_s(f)$: | + | ''Anmerkung:'' Die Leistung pro Bit ergibt sich als das Integral über ${\it Φ}_s(f)$: |
:$$P_{\rm S} = \int_{ - \infty }^\infty \hspace{-0.3cm} {{\it \Phi}_s(f)}\hspace{0.1cm} {\rm d}f | :$$P_{\rm S} = \int_{ - \infty }^\infty \hspace{-0.3cm} {{\it \Phi}_s(f)}\hspace{0.1cm} {\rm d}f | ||
= 2 \cdot \int_{ 0 }^\infty \hspace{-0.3cm} {\left [ C \cdot {\rm si}^2(\pi f T) + D \cdot \delta (f - f_{\rm T}]\right ]}\hspace{0.1cm} {\rm | = 2 \cdot \int_{ 0 }^\infty \hspace{-0.3cm} {\left [ C \cdot {\rm si}^2(\pi f T) + D \cdot \delta (f - f_{\rm T}]\right ]}\hspace{0.1cm} {\rm | ||
| Line 85: | Line 92: | ||
\,{\rm V^{2}}}.$$ | \,{\rm V^{2}}}.$$ | ||
| − | '''(3)''' Bei BPSK ist das Quellensignal $q(t)$ bipolar anzusetzen. Im Leistungsdichtespektrum fehlt deshalb die Diraclinie | + | |
| + | |||
| + | '''(3)''' Bei BPSK ist das Quellensignal $q(t)$ bipolar anzusetzen. | ||
| + | *Im Leistungsdichtespektrum fehlt deshalb die Diraclinie ⇒ $\underline{B = 0}$. | ||
| + | * Der kontinuierliche LDS–Anteil ist viermal so groß wie bei der ASK: | ||
:$$A = {s_0^2 \cdot T }\hspace{0.15cm}\underline { = 4 \cdot 10^{-6} \,{\rm V^{2}/Hz}}.$$ | :$$A = {s_0^2 \cdot T }\hspace{0.15cm}\underline { = 4 \cdot 10^{-6} \,{\rm V^{2}/Hz}}.$$ | ||
| + | |||
| + | |||
'''(4)''' Für die LDS–Parameter des BPSK–Sendesignals gilt analog zur ASK: | '''(4)''' Für die LDS–Parameter des BPSK–Sendesignals gilt analog zur ASK: | ||
:$$C = \frac {A}{4}\hspace{0.15cm}\underline { = 10^{-6} \,{\rm V^{2}/Hz}},\hspace{0.2cm}D = | :$$C = \frac {A}{4}\hspace{0.15cm}\underline { = 10^{-6} \,{\rm V^{2}/Hz}},\hspace{0.2cm}D = | ||
\frac {B}{4} \hspace{0.15cm}\underline {= 0}.$$ | \frac {B}{4} \hspace{0.15cm}\underline {= 0}.$$ | ||
| + | |||
| + | |||
'''(5)''' Richtig ist nur die <u>erste Aussage</u>: | '''(5)''' Richtig ist nur die <u>erste Aussage</u>: | ||
| − | * Bei BPSK (bipolares Quellensignal) beinhaltet ${\it Φ}_q(f)$ auch dann keine einzige Diraclinie, wenn $g_q(t)$ von der Rechteckform abweicht. | + | * Bei BPSK (bipolares Quellensignal) beinhaltet ${\it Φ}_q(f)$ auch dann keine einzige Diraclinie, wenn $g_q(t)$ von der Rechteckform abweicht (gleichwahrscheinliche Symbole vorausgesetzt). |
| − | *Dagegen beinhaltet das unipolare ASK–Quellensignal unendlich viele Diraclinien bei allen Vielfachen von $1/T$. | + | *Dagegen beinhaltet das unipolare ASK–Quellensignal unendlich viele Diraclinien bei allen Vielfachen von $1/T$. |
| + | |||
| − | Weitere Informationen | + | Weitere Informationen zu diesem Thema finden Sie auf der Seite „AKF und LDS bei unipolaren Binärsignalen” im Buch „Digitalsignalübertragung”. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 102: | Line 118: | ||
| − | [[Category: | + | [[Category:Modulation Methods: Exercises|^4.2 Lineare digitale Modulation^]] |
Revision as of 14:46, 23 March 2021
Die Sendesignale von ASK (Amplitude Shift Keying) und BPSK (Binary Phase Shift Keying) können beide in der Form
- $$s(t) = q(t) · z(t)$$
dargestellt werden, wobei $z(t)$ eine harmonische Schwingung mit der Frequenz $f_{\rm T}$ und der Amplitude $1$ darstellt. Die Trägerphase $ϕ_{\rm T}$ ist für die hier betrachteten Leistungsdichtespektren nicht von Bedeutung.
- Die Quelle ist jeweils redundanzfrei, was bedeutet, dass die beiden möglichen Symbole $±1$ gleichwahrscheinlich sind und die Symbole statistisch voneinander unabhängig.
- Bei ASK sind unipolare Amplitudenkoeffizienten – das heißt: $a_ν ∈ \{0, 1\}$ – des Quellensignals
- $$ q(t) = \sum_{\nu = - \infty}^{+\infty}a_\nu \cdot g_q (t - \nu \cdot T)$$
- anzusetzen, während im Fall der BPSK $a_ν ∈ \{-1, +1\}$ zu berücksichtigen ist.
In der Grafik sind die Leistungsdichtespektren ${\it Φ}_q(f)$ und ${\it Φ}_s(f)$ von Quellensignal und Sendesignal angegeben, die sich bei einem NRZ–Rechteckimpuls $g_q(t)$ mit der Amplitude $s_0 = 2 \ \rm V$ und der Dauer $T = 1 \ \rm µ s$ ergeben. Damit lautet die Spektralfunktion:
- $$G_q(f) = s_0 \cdot T \cdot {\rm si}(\pi f T)\hspace{0.05cm}.$$
Zu bestimmen sind die Konstanten $A$, $B$, $C$ und $D$ für die Modulationsverfahren $\rm ASK$ und $\rm BPSK$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Lineare digitale Modulation.
- Bezug genommen wird aber auch auf das Kapitel Grundlagen der codierten Übertragung im Buch „Digitalsignalübertragung”.
- Die Leistungen sind in $\rm V^2$ anzugeben; sie beziehen sich somit auf den Bezugswiderstand $R = 1 \ \rm \Omega$.
Fragebogen
Musterlösung
- Ohne diesen Gleichanteil ergäbe sich das stochastische Rechtecksignal $q(t) - m_q ∈ \{+s_0/2, -s_0/2\}$.
- Dieses gleichsignalfreie Signal besitzt den kontinuierlichen LDS–Anteil $(s_0/2)^2 · T · {\rm si}^2(πfT)$.
- Hieraus lässt sich der gesuchte Wert bei der Frequenz $f = 0$ ermitteln:
- $$A = \frac {s_0^2 \cdot T }{4} = \frac {(2\,{\rm V})^2 \cdot 10^{-6} \,{\rm s}}{4}\hspace{0.15cm}\underline {= 10^{-6} \,{\rm V^{2}/Hz}}.$$
(2) Das Spektrum $Z(f)$ eines Cosinussignals $z(t)$ besteht aus zwei Diracfunktionen bei $\pm f_{\rm T}$, jeweils mit dem Gewicht $1/2$.
- Das Leistungsdichtespektrum ${\it Φ}_z(f)$ besteht ebenfalls aus den beiden Diracfunktionen, nun aber mit jeweiligem Gewicht $1/4$.
- Die Faltung ${\it Φ}_q(f) ∗ {\it Φ}_z(f)$ ergibt das Leistungsdichtespektrum ${\it Φ}_s(f)$ des Sendesignals. Daraus folgt:
- $$C = {A}/{4} \hspace{0.15cm}\underline { = 0.25 \cdot 10^{-6} \,{\rm V^{2}/Hz}},\hspace{0.2cm}D = {B}/{4}\hspace{0.15cm}\underline { = 0.25 \,{\rm V^{2}}}.$$
Anmerkung: Die Leistung pro Bit ergibt sich als das Integral über ${\it Φ}_s(f)$:
- $$P_{\rm S} = \int_{ - \infty }^\infty \hspace{-0.3cm} {{\it \Phi}_s(f)}\hspace{0.1cm} {\rm d}f = 2 \cdot \int_{ 0 }^\infty \hspace{-0.3cm} {\left [ C \cdot {\rm si}^2(\pi f T) + D \cdot \delta (f - f_{\rm T}]\right ]}\hspace{0.1cm} {\rm d}f= 2 \cdot \left [ \frac{C}{T} + D \right ] = 2 \cdot \left [ \frac{0.25 \cdot 10^{-6} \,{\rm V^{2}/Hz}}{10^{-6} \,{\rm s}} + 0.25 \,{\rm V^{2}} \right ] \hspace{0.15cm}\underline {= 1 \,{\rm V^{2}}}.$$
(3) Bei BPSK ist das Quellensignal $q(t)$ bipolar anzusetzen.
- Im Leistungsdichtespektrum fehlt deshalb die Diraclinie ⇒ $\underline{B = 0}$.
- Der kontinuierliche LDS–Anteil ist viermal so groß wie bei der ASK:
- $$A = {s_0^2 \cdot T }\hspace{0.15cm}\underline { = 4 \cdot 10^{-6} \,{\rm V^{2}/Hz}}.$$
(4) Für die LDS–Parameter des BPSK–Sendesignals gilt analog zur ASK:
- $$C = \frac {A}{4}\hspace{0.15cm}\underline { = 10^{-6} \,{\rm V^{2}/Hz}},\hspace{0.2cm}D = \frac {B}{4} \hspace{0.15cm}\underline {= 0}.$$
(5) Richtig ist nur die erste Aussage:
- Bei BPSK (bipolares Quellensignal) beinhaltet ${\it Φ}_q(f)$ auch dann keine einzige Diraclinie, wenn $g_q(t)$ von der Rechteckform abweicht (gleichwahrscheinliche Symbole vorausgesetzt).
- Dagegen beinhaltet das unipolare ASK–Quellensignal unendlich viele Diraclinien bei allen Vielfachen von $1/T$.
Weitere Informationen zu diesem Thema finden Sie auf der Seite „AKF und LDS bei unipolaren Binärsignalen” im Buch „Digitalsignalübertragung”.