Aufgaben:Exercise 1.1: Simple Filter Functions

• Return to book

Considered quadripoles

A filter with the frequency response

$$H_{\rm TP}(f) = \frac{1}{1+ {\rm j}\cdot f/f_0}$$

is described as a low-pass filter of first order. Out of it, a first order high-pass filter can be designed according to the following rule:

$$H_{\rm HP}(f) = 1- H_{\rm TP}(f) .$$

In both cases  $f_0$  represents the so-called  $\text{3 dB}$–cutoff frequency.

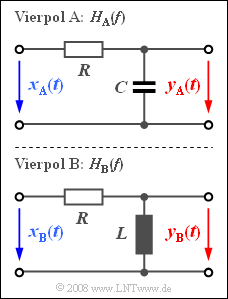
The figure shows two quadripoles  $\rm A$  and  $\rm B$. The task is to clarify which of the two quadripoles has a low-pass characteristic and which has a high-pass characteristic.

The components of circuit  $\rm A$  are given as follows:

$$R = 50 \,\, {\rm \Omega}, \hspace{0.2cm} C = 637 \,\, {\rm nF} .$$

The inductivity  $L$  of circuit  $\rm B$  is to be computed in subtask  (6) .

Please note:

• The task belongs to the chapter  Systembeschreibung im Frequenzbereich.
• For the subtask  (4)  cosine-shaped input signals are assumed. The frequency  $f_x$  is variable, the power is  $P_x = 10\,{\rm mW}.$

Questions

1

Compute the frequency response  $H_{\rm A}(f)$  of the quadripole  $\rm A$  and check the following statements.

	Quadripole  $\rm A$  is a low-pass filter.
	Quadripole  $\rm A$  is a high-pass filter.

2

Compute the reference frequency  $f_0$  from the components  $R$  and  $C$.

$f_0 \ = \ $  $\text{kHz}$

3

Compute the amplitude response  $|H_{\rm A}(f)|$. What are the numerical values for  $f = f_0$  and  $f = 2f_0$?

$|H_{\rm A}(f = f_0)|\ = \ $

$|H_{\rm A}(f = 2f_0)|\ = \ $

4

What is the power  $P_y$  of the output signal  $y(t)$ if a cosine signal of frequency  $f_x = 5\,{\rm kHz}$  or  $f_x = 10\,{\rm kHz}$  is applied to the input?

$P_y(f_x = 5 \ \rm kHz)\ = \ $  $\text{mW}$

$P_y(f_x = 10 \ \rm kHz)\ = \ $  $\text{mW}$

5

Compute the amplitude response  $|H_{\rm B}(f)|$  of the quadripole  $\rm B$  with the components  $R$  and  $L$  using the reference frequency  $f_0 = R/(2πL)$.
What are the values for  $f = 0$,  $f = f_0$, $f = 2f_0$  and for  $f → ∞$?

$|H_{\rm B}(f = 0)|\ = \ $

$|H_{\rm B}(f = f_0)|\ = \ $

$|H_{\rm B}(f = 2f_0)|\ = \ $

$|H_{\rm B}(f → ∞)|\ = \ $

6

What inductivity  $L$  results in the reference frequency  $f_0 = 5 \,\text{kHz}$?

$L\ = \ $  $\text{mH}$

Sample solution

Solution

(1)  Approach 1 is correct:

• Der komplexe Widerstand der Kapazität  $C$  ist gleich  $1/({\rm j}ωC)$, wobei  $ω = 2πf$  die so genannte Kreisfrequenz angibt.
• Der Frequenzgang lässt sich nach dem Spannungsteilerprinzip berechnen:

$$H_{\rm A}(f) = \frac{Y_{\rm A}(f)}{X_{\rm A}(f)} = \frac{1/({\rm j}\omega C)}{R+1/({\rm j}\omega C)}=\frac{1}{1+{\rm j \cdot 2\pi}\cdot f \cdot R\cdot C}.$$

• Wegen  $H_{\rm A}(f = 0) = 1$  kann dies kein Hochpass sein; vielmehr handelt es sich um einen Tiefpass.
• Bei niedrigen Frequenzen ist der Blindwiderstand der Kapazität sehr groß und es gilt  $y_{\rm A}(t) ≈ x_{\rm A}(t)$.
• Dagegen wirkt der Kondensator bei sehr hohen Frequenzen wie ein Kurzschluss und es ist  $y_{\rm A}(t) ≈ 0$.

(2)  Durch Koeffizientenvergleich zwischen  $H_{\rm TP}(f)$  auf der Angabenseite und  $H_{\rm A}(f)$  gemäß Teilaufgabe  (1)  erhält man:

$$f_0 = \frac{1}{2\pi \cdot R \cdot C} = \frac{1}{2\pi \cdot{\rm 50\hspace{0.05cm} \Omega}\cdot {\rm 637 \cdot 10^{-9}\hspace{0.05cm} s/\Omega}}\hspace{0.15cm}\underline{\approx 5 \, {\rm kHz}}.$$

(3)  Der Amplitudengang lautet:

$$|H_{\rm A}(f)| = \frac{1}{\sqrt{1+ (f/f_0)^2}}.$$

• Für  $f = f_0$  erhält man den Zahlenwert  $1/\sqrt{2}\hspace{0.1cm} \underline{≈ 0.707}$, und
• für  $f = 2f_0$  näherungsweise den Wert  $1/\sqrt{5}\hspace{0.1cm} \underline{≈ 0.477}$.

(4)  Die Ausgangsleistung kann nach folgender Gleichung berechnet werden:

$$P_y = P_x \cdot |H_{\rm A}(f = f_x)|^2.$$

• Für  $f_x = f_0$  ist  $P_y = P_x/2 \hspace{0.1cm} \underline{ = 5\hspace{0.1cm} {\rm mW}}$, also ergibt sich am Ausgang nur noch die halbe Leistung.

• In logarithmischer Darstellung lautet diese Beziehung:

$$10 \cdot {\rm lg}\hspace{0.2cm} \frac{P_x(f_0)}{P_y(f_0)} = 3\,{\rm dB}.$$

Deshalb ist für  $f_0$  auch die Bezeichnung "3dB–Grenzfrequenz" üblich.

• Für  $f_x = 2f_0$  erhält man dagegen einen kleineren Wert:  $P_y = P_x/5 \hspace{0.1cm}\underline{= 2\hspace{0.1cm} {\rm mW}}$.

(5)  Analog zur Teilaufgabe  (1)  gilt:

$$H_{\rm B}(f) = \frac{Y_{\rm B}(f)}{X_{\rm B}(f)} = \frac{{\rm j}\omega L}{R+{\rm j}\omega L}=\frac{{\rm j2\pi}\cdot f \cdot L/R}{1+{\rm j2\pi}\cdot f \cdot L/R}.$$

• Unter Verwendung der Bezugsfrequenz  $f_0 = R/(2πL)$  kann hierfür auch geschrieben werden:

$$H_{\rm B}(f) = \frac{{\rm j}\cdot f/f_0}{1+{\rm j}\cdot f/f_0}\hspace{0.5cm}\Rightarrow \hspace{0.5cm}|H_{\rm B}(f)| = \frac{|f/f_0|}{\sqrt{1+ (f/f_0)^2}}.$$

• Daraus erhält man die Zahlenwerte:

$$|H_{\rm B}(f = 0)| \hspace{0.15cm}\underline{= 0}, \hspace{0.5cm} |H_{\rm B}( f_0)| \hspace{0.15cm}\underline{=0.707}, \hspace{0.5cm}|H_{\rm B}(2f_0)| \hspace{0.15cm}\underline{= 0.894}, \hspace{0.5cm}|H_{\rm B}(f \rightarrow \infty)|\hspace{0.15cm}\underline{ = 1}.$$

• Der Vierpol $\rm B$ ist demzufolge ein Hochpass.

(6)  Aus obiger Definition der Bezugsfrequenz folgt:

$$L = \frac{R}{2\pi \cdot f_0} = \frac{{\rm 50\hspace{0.05cm} \Omega}}{2\pi \cdot{\rm 5000 \hspace{0.05cm} Hz}}= {\rm 1.59 \cdot 10^{-3}\hspace{0.05cm} \Omega s}\hspace{0.15cm}\underline{= {\rm 1.59 \hspace{0.1cm} mH}} .$$