Difference between revisions of "Aufgaben:Exercise 1.2Z: Lognormal Fading Revisited"
| Line 4: | Line 4: | ||
[[File:P_ID2123__Mob_Z_1_2.png|right|frame|Pfadverlustmodell <br>mit Lognormal-Fading]] | [[File:P_ID2123__Mob_Z_1_2.png|right|frame|Pfadverlustmodell <br>mit Lognormal-Fading]] | ||
| − | We assume similar conditions as in | + | We assume similar conditions as in [[Aufgaben:Exercise_1.2__Lognormal_Channel_Model|Task 1. 2]] but now we summarize the purely distance-dependent path loss $V_0$ and the mean value $m_{\rm S}$ of the lognormal–fading (the index „S” stands for <i>Shadowing</i>): |
$$V_{\rm 1} = V_{\rm 0} + m_{\rm S} \hspace{0.05cm}.$$ | $$V_{\rm 1} = V_{\rm 0} + m_{\rm S} \hspace{0.05cm}.$$ | ||
Revision as of 17:17, 25 March 2020
We assume similar conditions as in Task 1. 2 but now we summarize the purely distance-dependent path loss $V_0$ and the mean value $m_{\rm S}$ of the lognormal–fading (the index „S” stands for Shadowing): $$V_{\rm 1} = V_{\rm 0} + m_{\rm S} \hspace{0.05cm}.$$
The total path loss is then given by the equation $$V_{\rm P} = V_{\rm 1} + V_{\rm 2}(t)$$
where $V_2(t)$ describes a lognormal–distribution with mean value zero: $$f_{V{\rm 2}}(V_{\rm 2}) = \frac {1}{ \sqrt{2 \pi }\cdot \sigma_{\rm S}} \cdot {\rm exp } \left [ - \frac{ V_{\rm 2} ^2}{2 \cdot \sigma_{\rm S}^2} \right ] \hspace{0.05cm}.$$
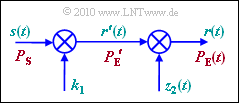
The path loss model shown in the graphic is suitable for the scenario described here:
- Multiply the transmitted signal $s(t)$ first with a constant factor $k_1$ and further with a stochastic quantity $z_2(t)$ with the probability density (WDF) $f_{\rm z2}(z_2)$, then the signal $r(t)$ results at the output, whose power $P_{\rm E}(t)$ is of course also time-dependent due to the stochastic component.
- The WDF of the lognormally distributed random variable $z_2$ is for $z_2 ≥ 0$:
$$f_{z{\rm 2}}(z_{\rm 2}) = \frac {{\rm exp } \left [ - {\rm ln}^2 (z_{\rm 2}) /({2 \cdot C^2 \cdot \sigma_{\rm S}^2}) \right ]}{ \sqrt{2 \pi }\cdot C \cdot \sigma_{\rm S} \cdot z_2} \hspace{0.3cm}{\rm with} \hspace{0.3cm} C = \frac{{\rm ln} \hspace{0.1cm}(10)}{20\,\,{\rm dB}}\hspace{0.05cm}.$$
- For $z_2 ≤ 0$ this WDF is equal to zero.
Notes:
- The task belongs to the chapter Distance-dependent attenuation and shading.
- Use the following parameters:
$$V_{\rm 1} = 60\,{\rm dB}\hspace{0.05cm},\hspace{0.2cm} \sigma_{\rm S} = 6\,{\rm dB}\hspace{0.05cm}.$$
- The probability that a mean-free Gaussian random variable $z$ is greater than its dispersion $\sigma$, is
$${\rm Pr}(z > \sigma) = {\rm Pr}(z < -\sigma) = {\rm Q}(1) \approx 0.158\hspace{0.05cm}.$$
- Also applies: ${\rm Pr}(z > 2\sigma) = {\rm Pr}(z < -2\sigma) = {\rm Q}(2) \approx 0.023\hspace{0.05cm}.$
- Again for clarification: $z_2$ is the linear fading–size, while the description size $V_2$ is based on the tenner–logarithm.
- The following conversions apply:
$$z_2 = 10^{-V_{\rm 2}/20\,{\rm dB}}\hspace{0.05cm}, \hspace{0.2cm} V_{\rm 2} = -20\,{\rm dB} \cdot {\rm lg}\hspace{0.15cm}z_2\hspace{0.05cm}.$ ==='"`UNIQ--h-0--QINU`"'Questionnaire=== '"`UNIQ--quiz-00000002-QINU`"' ==='"`UNIQ--h-1--QINU`"'Sample solution=== '"`UNIQ--html-00000003-QINU`"' '''(1)''' The constant $k_1$ generates the time-independent path loss $V_1 = 60 \ \rm dB$. From this follows: $$k_{\rm 1} = 10^{-V_{\rm 1}/(20\hspace{0.05cm} {\rm dB})} \hspace{0.15cm} \underline{= 0.001}\hspace{0.05cm}.$$ '''(2)''' Correct is only the <u>second solution suggestion</u>: *For the Gaussian random variable $V_2$ all values between $–∞$ and $+∞$ are (theoretically) possible. *The transformation $z_2 = 10^{{\it –V_2}\rm /20}$ results in only positive values for the linear random variable $z_2$, namely between 0 (if $V_2$ is positive and reaches to infinity) and $+∞$ (very large negative values of $V_2$). '''(3)'' The random value $z_2$ can only be positive. Therefore the WDF–value $f_{\rm z2}(z_2 = 0)\hspace{0.15cm} is \underline{ = 0}$. *Der WDF–Wert für den Abszissenwert $z_2 = 1$ erhält man durch Einsetzen in die gegebene Gleichung: :$$f_{z{\rm 2}}(z_{\rm 2} = 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac {{\rm exp } \left [ - {\rm ln}^2 (z_2 = 1) /({2 \cdot C^2 \cdot \sigma_{\rm S}^2}) \right ]}{ \sqrt{2 \pi }\cdot C \cdot \sigma_{\rm S} \cdot (z_2 = 1)}=\frac {1}{ \sqrt{2 \pi } \cdot \sigma_{\rm S} } \cdot \frac {1}{ C } =
\frac {1}{ \sqrt{2 \pi } \cdot 6\,\,{\rm dB} } \cdot \frac {20\,\,{\rm dB}}{ {\rm ln} \hspace{0.1cm}(10) }
\hspace{0.15cm} \underline{\approx 0.578}\hspace{0.05cm}.$$
*Der erste Anteil ist gleich dem WDF–Wert $f_{{\it V}2}(V_2 = 0)$.
*$C$ berücksichtigt den Betrag der Ableitung der nichtlinearen Kennlinie $z_2 = g(V_2)$ für $V_2 = 0 \ \rm dB$ bzw. $z_2 = 1$.
*Schließlich erhält man für $z_2 = 2$:
:$$f_{z{\rm 2}}(z_{\rm 2} = 2) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac {f_{z{\rm 2}}(z_{\rm 2} = 1)}{ z_{\rm 2} = 2} \cdot
{\rm exp } \left [ - \frac {{\rm ln}^2 (2)}{2 \cdot C^2 \cdot \sigma_{\rm S}^2} \right ]= \frac {0.578}{ 2} \cdot
{\rm exp } \left [ - \frac {0.48}{0.952} \right ] \hspace{0.15cm} \underline{\approx 0.174}\hspace{0.05cm}. $$
'''(4)''' Berücksichtigt man den Zusammenhang zwischen $z_2$ und $V_2$, so erhält man:
:$${\rm Pr}(z_{\rm 2} > 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(V_{\rm 2} < 0\,\,{\rm dB})\hspace{0.15cm} \underline{= 0.5}
\hspace{0.05cm},$$
:$${\rm Pr}(z_{\rm 2} > 0.5) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(V_{\rm 2} < 6\,\,{\rm dB}) = 1- {\rm Pr}(V_{\rm 2} > 6\,\,{\rm dB})= 1- {\rm Pr}(V_{\rm 2} > \sigma_{\rm S})= 1- {\rm Q}(1)\hspace{0.15cm} \underline{= 0.842}
\hspace{0.05cm},$$
:$${\rm Pr}(z_{\rm 2} > 4) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(V_{\rm 2} < -12\,\,{\rm dB}) = {\rm Pr}(V_{\rm 2} > +12\,\,{\rm dB}) = {\rm Pr}(V_{\rm 2} > 2 \sigma_{\rm S})
\hspace{0.05cm}.$$
*Die Wahrscheinlichkeit, dass eine Gaußvariable größer ist als $2 \cdot \sigma$, ist aber gleich ${\rm Q}(2)$:
:$${\rm Pr}(z_{\rm 2} > 4) = {\rm Q}(2)\hspace{0.15cm} \underline{= 0.023}
\hspace{0.05cm}.$$
'''(5)''' Richtig ist der <u>Lösungsvorschlag 3</u>:
*Die erste Aussage ist mit Sicherheit nicht zutreffend, da sich der Mittelwert $m_{\rm S}$ auf die logarithmierte Empfangsleistung (in $\rm dBm$) bezieht.
*Um zu klären, ob nun die zweite oder die dritte Lösungsalternative zutrifft, gehen wir von $P_{\rm S} = 1 \ \rm W$, $V_1 = 60 \ \rm dB$ ⇒ $P_{\rm E}' = 1 \ {\rm µ W}$ und folgender $V_2$–WDF aus:
:$$f_{V{\rm 2}}(V_{\rm 2}) = 0.5 \cdot \delta (V_{\rm 2}) + 0.25 \cdot \delta (V_{\rm 2}- 10\,\,{\rm dB})
+ 0.25 \cdot \delta (V_{\rm 2}+ 10\,\,{\rm dB})\hspace{0.05cm}.$$
*In der Hälfte der Zeit ist dann $P_{\rm E} = 1 \ \rm µ W$, während in den beiden anderen Vierteln jeweils gilt:
:$$V_{\rm 2}= +10\,\,{\rm dB}\text{:} \hspace{0.3cm} P_{\rm E}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1\,\,{\rm W}}{10^7} = 0.1\,\,{\rm µ W}\hspace{0.05cm},$$
:$$V_{\rm 2}= -10\,\,{\rm dB}\text{:} \hspace{0.3cm} P_{\rm E}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1\,\,{\rm W}}{10^5} = 10\,\,{\rm µ W}\hspace{0.05cm}.$$
*Der Mittelwert ergibt somit:
:$${\rm E}[P_{\rm E}(t)] = 0.5 \cdot 1\,{\rm µ W}+ 0.25 \cdot 0.1\,{\rm µ W}+0.25 \cdot 10\,{\rm µ W}= 3.025\,{\rm µ W} > P_{\rm E}\hspace{0.05cm}' = 1\,{\rm µ W}
\hspace{0.05cm}.$$
*Diese einfache Rechnung mit diskreten Wahrscheinlichkeiten anstelle einer kontinuierlichen WDF deutet darauf hin, dass der <u>Lösungsvorschlag 3</u> richtig sein wird.
*The WDF–value for the abscissa value $z_2 = 1$ is obtained by inserting it into the given equation:
$$f_{z{\rm 2}}(z_{\rm 2} = 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac {\rm exp } \left [ - {\rm ln}^2 (z_2 = 1) /({2 \cdot C^2 \cdot \sigma_{\rm S}^2}) \right ]}{ \sqrt{2 \pi }\cdot C \cdot \sigma_{\rm S} \cdot (z_2 = 1)}=\frac {1}{ \sqrt{2 \pi } \cdot \sigma_{\rm S} } \cdot \frac {1}{C } =
\frac {1}{ \sqrt{2 \pi } \cdot 6\,\,{\rm dB} } \cdot \frac {20\,\,{\rm dB}}}{ {\rm ln} \hspace{0.1cm}(10) }
\hspace{0.15cm} \underline{\approx 0.578}\hspace{0.05cm}.$$
*The first portion is equal to the WDF–value $f_{{{\it V}2}(V_2 = 0)$.
*$C$ considers the amount of the derivative of the non-linear characteristic $z_2 = g(V_2)$ for $V_2 = 0 \ \rm dB$ or $z_2 = 1$.
*Finally, for $z_2 = 2$:
$$f_{z{\rm 2}}(z_{\rm 2} = 2) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac {f_{z{\rm 2}}}(z_{\rm 2} = 1)}{ z_{\rm 2} = 2} \cdot
{\rm exp } \left [ - \frac {{{\rm ln}^2 (2)}{2 \cdot C^2 \cdot \sigma_{\rm S}^2} \right ]= \frac {0.578}{ 2} \cdot
{\rm exp } \left [ - \frac {0.48}{0.952} \right ] \hspace{0.15cm} \underline{\approx 0.174}\hspace{0.05cm}. $$
'''(4)''' If you take into account the relationship between $z_2$ and $V_2$, you get
$${\rm Pr}(z_{\rm 2} > 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(V_{\rm 2} < 0\,\,{\rm dB})\hspace{0.15cm} \underline{= 0.5}
\hspace{0.05cm},$$
$${\rm Pr}(z_{\rm 2} > 0.5) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(V_{\rm 2} < 6\,\,{\rm dB}) = 1- {\rm Pr}(V_{\rm 2} > 6\,\,{\rm dB})= 1- {\rm Pr}(V_{\rm 2} > \sigma_{\rm S})= 1- {\rm Q}(1)\hspace{0.15cm} \underline{= 0.842}
\hspace{0.05cm},$$
$${\rm Pr}(z_{\rm 2} > 4) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(V_{\rm 2} < -12\,\,{\rm dB}) = {\rm Pr}(V_{\rm 2} > +12\,\,{\rm dB}) = {\rm Pr}(V_{\rm 2} > 2 \sigma_{\rm S})
\hspace{0.05cm}.$$
*The probability that a Gaussian variable is greater than $2 \cdot \sigma$, but equals ${\rm Q}(2)$:
$${\rm Pr}(z_{\rm 2} > 4) = {\rm Q}(2)\hspace{0.15cm} \underline{= 0.023}
\hspace{0.05cm}.$$
'''(5)''' Correct is the <u>solution 3</u>:
*The first statement is certainly not correct, since the mean value $m_{\rm S}$ refers to the logarithmic received power (in $\rm dBm$).
*To clarify whether the second or the third solution alternative is correct, we assume $P_{\rm S} = 1 \ \ \rm W$, $V_1 = 60 \ \ \rm dB$ ⇒ $P_{\rm E}' = 1 \ {\rm µ W}$ and the following $V_2$–WDF
$$f_{V{\rm 2}}(V_{\rm 2}) = 0.5 \cdot \delta (V_{\rm 2}) + 0.25 \cdot \delta (V_{\rm 2}- 10\,\,{\rm dB})
+ 0.25 \cdot \delta (V_{\rm 2}+ 10\,\,{\rm dB})\hspace{0.05cm}.$
*Halfway through the time, $P_{\rm E} = 1 \ \ \rm µ W$, while in the other two quarters, each is valid:
$$V_{\rm 2}= +10\,\,{\rm dB}\text{:} \hspace{0.3cm} P_{\rm E}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1\,\,{\rm W}}{10^7} = 0.1\,\,{\,}{\rm µ W}\hspace{0.05cm},$$ $$V_{\rm 2}= -10\,\,{\,}{\rm dB}\text{:} \hspace{0.3cm} P_{\rm E}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1\,\,{\rm W}}{10^5} = 10\,\,{\,}{\rm µ W}\hspace{0.05cm}.$$
- The mean value thus gives:
$${\rm E}[P_{\rm E}(t)] = 0.5 \cdot 1\,{\rm µ W}+ 0.25 \cdot 0.1\,{\rm µ W}+ 0.25 \cdot 10\,{\rm µ W}= 3.025\,{\rm µ W} > P_{\rm E}\hspace{0.05cm}' = 1\,{\rm µ W} \hspace{0.05cm}.$$
- This simple calculation with discrete probabilities instead of a continuous WDF indicates that the solution 3 will be correct.