Difference between revisions of "Aufgaben:Exercise 1.4: 2S/3E Channel Model"
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Statistical_Dependence_and_Independence}} |
| − | }} | ||
| − | [[File:EN_Sto_A_1_4.png|right|frame|$\rm 2S/3E$ | + | [[File:EN_Sto_A_1_4.png|right|frame|$\rm 2S/3E$ channel model]] |
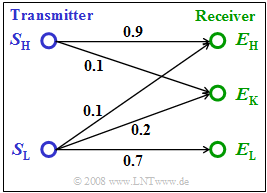
| − | + | A transmitter emits the binary symbols $\rm L$ $($event $S_{\rm L})$ and $\rm H$ $($event $S_{\rm H})$ . | |
| − | * | + | *If conditions are good, the digital receiver also decides only on the binary symbols $\rm L$ $($Ereignis $E_{\rm L})$ or $\rm H$ $($event $E_{\rm H})$. |
| − | * | + | *However, if the receiver can suspect that an error has occurred during transmission, it makes no decision $($event $E_{\rm K})$; $\rm K$ here stands for "No decision"). |
| − | + | The diagram shows a simple channel model in terms of transition probabilities. It can be seen that a transmitted $\rm L$ may well be received as a symbol $\rm H$ . In contrast, the transition from $\rm H$ to $\rm L$ is not possible. | |
| − | + | Let the symbol appearance probabilities at the transmitter be ${\rm Pr}(S_{\rm L}) = 0.3$ and ${\rm Pr}(S_{\rm H}) = 0.7$. | |
| Line 19: | Line 18: | ||
| − | + | Hints: | |
| − | * | + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Statistical_Dependence_and_Independence|Statistical dependence and independence]]. |
| − | * | + | *The topic of this chapter is illustrated with examples in the (German language) learning video |
| + | :[[Statistische_Abhängigkeit_und_Unabhängigkeit_(Lernvideo)|Statistische Abhängigkeit und Unabhängigkeit]] $\Rightarrow$ "Statistical dependence and independence". | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the probability that the receiver chooses the symbol $\rm L$ ? |
|type="{}"} | |type="{}"} | ||
${\rm Pr}(E_{\rm L}) \ = \ $ { 0.21 3% } | ${\rm Pr}(E_{\rm L}) \ = \ $ { 0.21 3% } | ||
| − | { | + | {What is the probability that the receiver chooses the symbo $\rm H$ ? |
|type="{}"} | |type="{}"} | ||
${\rm Pr}(E_{\rm H}) \ = \ $ { 0.66 3% } | ${\rm Pr}(E_{\rm H}) \ = \ $ { 0.66 3% } | ||
| − | { | + | {What is the probability that the receiver does not make a decision? |
|type="{}"} | |type="{}"} | ||
${\rm Pr}(E_{\rm K}) \ = \ $ { 0.13 3% } | ${\rm Pr}(E_{\rm K}) \ = \ $ { 0.13 3% } | ||
| − | { | + | {What is the probability that the receiver makes a wrong decision? |
|type="{}"} | |type="{}"} | ||
$\text{Pr(falsche Entscheidung)} \ = \ $ { 0.03 3% } | $\text{Pr(falsche Entscheidung)} \ = \ $ { 0.03 3% } | ||
| − | { | + | {What is the probability that symbol $\rm L$ was actually sent if the receiver decided to use symbol $\rm L$ ? |
|type="{}"} | |type="{}"} | ||
${\rm Pr}(S_{\rm L}\hspace{0.05cm}|\hspace{0.05cm}E_{\rm L} ) \ = \ $ { 1 3% } | ${\rm Pr}(S_{\rm L}\hspace{0.05cm}|\hspace{0.05cm}E_{\rm L} ) \ = \ $ { 1 3% } | ||
| − | { | + | {What is the probability that symbol $\rm L$ was sent if the receiver does not make a decision? |
|type="{}"} | |type="{}"} | ||
${\rm Pr}(S_{\rm L}\hspace{0.05cm}|\hspace{0.05cm}E_{\rm K} ) \ =\ $ { 0.4614 3% } | ${\rm Pr}(S_{\rm L}\hspace{0.05cm}|\hspace{0.05cm}E_{\rm K} ) \ =\ $ { 0.4614 3% } | ||
| Line 61: | Line 61: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Only if the symbol $\rm L$ was sent, the receiver can decide for the symbol $\rm L$ at the given channel. |
| − | * | + | *However, the probability for a received $\rm L$ is smaller by a factor of $0.7$ than for a sent one. From this follows: |
:$${\rm Pr} (E_{\rm L}) = {\rm Pr}(S_{\rm L}) \cdot {\rm Pr} (E_{\rm L}\hspace{0.05cm}|\hspace{0.05cm}S_{\rm L}) = 0.3 \cdot 0.7 \hspace{0.15cm}\underline {= \rm 0.21}.$$ | :$${\rm Pr} (E_{\rm L}) = {\rm Pr}(S_{\rm L}) \cdot {\rm Pr} (E_{\rm L}\hspace{0.05cm}|\hspace{0.05cm}S_{\rm L}) = 0.3 \cdot 0.7 \hspace{0.15cm}\underline {= \rm 0.21}.$$ | ||
| − | '''(2)''' | + | '''(2)''' To the event $E_{\rm H}$ one comes from $S_{\rm H}$ as well as from $S_{\rm L}$ . Therefore holds: |
:$${\rm Pr} (E_{\rm H}) = {\rm Pr} (S_{\rm H}) \cdot {\rm Pr} (E_{\rm H}\hspace{0.05cm}|\hspace{0.05cm}S_{\rm H}) + {\rm Pr} (S_{\rm L}) \cdot {\rm Pr} (E_{\rm H}\hspace{0.05cm}|\hspace{0.05cm} S_{\rm L})= \rm 0.7 \cdot 0.9 + 0.3 \cdot 0.1\hspace{0.15cm}\underline { = \rm 0.66}.$$ | :$${\rm Pr} (E_{\rm H}) = {\rm Pr} (S_{\rm H}) \cdot {\rm Pr} (E_{\rm H}\hspace{0.05cm}|\hspace{0.05cm}S_{\rm H}) + {\rm Pr} (S_{\rm L}) \cdot {\rm Pr} (E_{\rm H}\hspace{0.05cm}|\hspace{0.05cm} S_{\rm L})= \rm 0.7 \cdot 0.9 + 0.3 \cdot 0.1\hspace{0.15cm}\underline { = \rm 0.66}.$$ | ||
| − | '''(3)''' | + | '''(3)''' The events $E_{\rm H}$, $E_{\rm L}$ and $E_{\rm K}$ together form a complete system. It follows that: |
:$${\rm Pr} (E_{\rm K}) = 1 - {\rm Pr} (E_{\rm L}) - {\rm Pr} (E_{\rm H}) \hspace{0.15cm}\underline {= \rm 0.13}.$$ | :$${\rm Pr} (E_{\rm K}) = 1 - {\rm Pr} (E_{\rm L}) - {\rm Pr} (E_{\rm H}) \hspace{0.15cm}\underline {= \rm 0.13}.$$ | ||
| − | '''(4)''' | + | '''(4)''' A wrong decision can be characterized in set-theoretic terms as follows: |
| − | |||
| + | :$${\rm Pr} \text{(wrong decision)} = {\rm Pr} \big [(S_{\rm L} \cap E_{\rm H}) \cup (S_{\rm H} \cap E_{\rm L})\big ] = \rm 0.3 \cdot 0.1 + 0.7\cdot 0 \hspace{0.15cm}\underline {= \rm 0.03}.$$ | ||
| − | '''(5)''' | + | |
| + | '''(5)''' If the symbol $\rm L$ was received, only $\rm L$ could have been sent. It follows that: | ||
:$${\rm Pr} (S_{\rm L} \hspace{0.05cm}|\hspace{0.05cm} E_{\rm L}) \hspace{0.15cm}\underline {= \rm 1}.$$ | :$${\rm Pr} (S_{\rm L} \hspace{0.05cm}|\hspace{0.05cm} E_{\rm L}) \hspace{0.15cm}\underline {= \rm 1}.$$ | ||
| − | '''(6)''' | + | '''(6)''' For example, Bayes' theorem is suitable for solving this problem: |
:$${\rm Pr} (S_{\rm L}\hspace{0.05cm}|\hspace{0.05cm} E_{\rm K}) =\frac{ {\rm Pr} ( E_{\rm K} \hspace{0.05cm}|\hspace{0.05cm} S_{\rm L}) \cdot {\rm Pr} (S_{\rm L})}{{\rm Pr} (E_{\rm K})} =\frac{ \rm 0.2 \cdot 0.3}{\rm 0.13} = \frac{\rm 6}{\rm 13}\hspace{0.15cm}\underline { \approx \rm 0.462}.$$ | :$${\rm Pr} (S_{\rm L}\hspace{0.05cm}|\hspace{0.05cm} E_{\rm K}) =\frac{ {\rm Pr} ( E_{\rm K} \hspace{0.05cm}|\hspace{0.05cm} S_{\rm L}) \cdot {\rm Pr} (S_{\rm L})}{{\rm Pr} (E_{\rm K})} =\frac{ \rm 0.2 \cdot 0.3}{\rm 0.13} = \frac{\rm 6}{\rm 13}\hspace{0.15cm}\underline { \approx \rm 0.462}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 21:56, 28 November 2021
A transmitter emits the binary symbols $\rm L$ $($event $S_{\rm L})$ and $\rm H$ $($event $S_{\rm H})$ .
- If conditions are good, the digital receiver also decides only on the binary symbols $\rm L$ $($Ereignis $E_{\rm L})$ or $\rm H$ $($event $E_{\rm H})$.
- However, if the receiver can suspect that an error has occurred during transmission, it makes no decision $($event $E_{\rm K})$; $\rm K$ here stands for "No decision").
The diagram shows a simple channel model in terms of transition probabilities. It can be seen that a transmitted $\rm L$ may well be received as a symbol $\rm H$ . In contrast, the transition from $\rm H$ to $\rm L$ is not possible.
Let the symbol appearance probabilities at the transmitter be ${\rm Pr}(S_{\rm L}) = 0.3$ and ${\rm Pr}(S_{\rm H}) = 0.7$.
Hints:
- The exercise belongs to the chapter Statistical dependence and independence.
- The topic of this chapter is illustrated with examples in the (German language) learning video
- Statistische Abhängigkeit und Unabhängigkeit $\Rightarrow$ "Statistical dependence and independence".
Questions
Solution
- However, the probability for a received $\rm L$ is smaller by a factor of $0.7$ than for a sent one. From this follows:
- $${\rm Pr} (E_{\rm L}) = {\rm Pr}(S_{\rm L}) \cdot {\rm Pr} (E_{\rm L}\hspace{0.05cm}|\hspace{0.05cm}S_{\rm L}) = 0.3 \cdot 0.7 \hspace{0.15cm}\underline {= \rm 0.21}.$$
(2) To the event $E_{\rm H}$ one comes from $S_{\rm H}$ as well as from $S_{\rm L}$ . Therefore holds:
- $${\rm Pr} (E_{\rm H}) = {\rm Pr} (S_{\rm H}) \cdot {\rm Pr} (E_{\rm H}\hspace{0.05cm}|\hspace{0.05cm}S_{\rm H}) + {\rm Pr} (S_{\rm L}) \cdot {\rm Pr} (E_{\rm H}\hspace{0.05cm}|\hspace{0.05cm} S_{\rm L})= \rm 0.7 \cdot 0.9 + 0.3 \cdot 0.1\hspace{0.15cm}\underline { = \rm 0.66}.$$
(3) The events $E_{\rm H}$, $E_{\rm L}$ and $E_{\rm K}$ together form a complete system. It follows that:
- $${\rm Pr} (E_{\rm K}) = 1 - {\rm Pr} (E_{\rm L}) - {\rm Pr} (E_{\rm H}) \hspace{0.15cm}\underline {= \rm 0.13}.$$
(4) A wrong decision can be characterized in set-theoretic terms as follows:
- $${\rm Pr} \text{(wrong decision)} = {\rm Pr} \big [(S_{\rm L} \cap E_{\rm H}) \cup (S_{\rm H} \cap E_{\rm L})\big ] = \rm 0.3 \cdot 0.1 + 0.7\cdot 0 \hspace{0.15cm}\underline {= \rm 0.03}.$$
(5) If the symbol $\rm L$ was received, only $\rm L$ could have been sent. It follows that:
- $${\rm Pr} (S_{\rm L} \hspace{0.05cm}|\hspace{0.05cm} E_{\rm L}) \hspace{0.15cm}\underline {= \rm 1}.$$
(6) For example, Bayes' theorem is suitable for solving this problem:
- $${\rm Pr} (S_{\rm L}\hspace{0.05cm}|\hspace{0.05cm} E_{\rm K}) =\frac{ {\rm Pr} ( E_{\rm K} \hspace{0.05cm}|\hspace{0.05cm} S_{\rm L}) \cdot {\rm Pr} (S_{\rm L})}{{\rm Pr} (E_{\rm K})} =\frac{ \rm 0.2 \cdot 0.3}{\rm 0.13} = \frac{\rm 6}{\rm 13}\hspace{0.15cm}\underline { \approx \rm 0.462}.$$