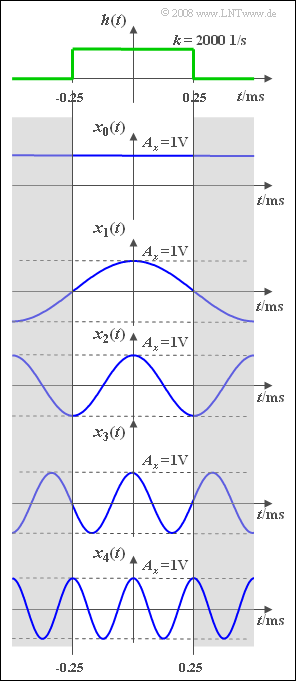
Exercise 1.6Z: Interpretation of the Frequency Response
The task is meant to investigate the influence of a low-pass filter $H(f)$ on cosinusoidal signals of the form
- $$x_i(t) = A_x \cdot {\rm cos}(2\pi f_i t ).$$
In the graph you can see the signals $x_i(t)$ where the index $i$ indicates the frequency in $\rm kHz$ . So, $x_2(t)$ describes a $2 \hspace{0.09cm} \rm kHz$–signal.
The signal amplitude in each case is $A_x = 1 \hspace{0.05cm} \rm V$. The direct (DC) signal $x_0(t)$ is to be interpreted as a limiting case of a cosine signal with frequeny $f_0 =0$.
The upper sketch shows the rectangular impulse response $h(t)$ of the low-pass filter. Its frequency response is:
- $$H(f) = {\rm si}(\pi {f}/{ {\rm \Delta}f}) .$$
Due to linearity and the fact that $H(f)$ is real and even the output signals are also cosine-shaped:
- $$y_i(t) = A_i \cdot {\rm cos}(2\pi f_i t ) .$$
- The signal amplitudes $A_i$ at the output for different frequencies $f_i$ are searched-for and the solution is to be found in the time domain only.
- This somewhat circuitous solution is intended to make the basic relationship between the time and frequency domains clear.
Please note:
- The exercise belongs to the chapter Some Low-Pass Functions in Systems Theory.
- Contrary to the usual definition of the amplitude, the "$A_i$" may well be negative. Then, this corresponds to the function "minus-cosine".
Questions
Solution
(2) The (equivalent) time duration of the impulse response is $Δt = 0.5 \ \rm ms$. The equivalent bandwidth is equal to the reciprocal:
- $$Δf = 1/Δt \ \rm \underline{= \ 2 \ kHz}.$$
(3) Approaches 1 and 3 are correct:
- The amplitude is $A_i = y_i(t = 0)$ since $y_i(t)$ is cosine-shaped. The output signal is calculated by convolution for this purpose:
- $$A_i = y_i (t=0) = \int\limits_{ - \infty }^{ + \infty } {x_i ( \tau )} \cdot h ( {0 - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$
- Considering the symmetry and the time limitation of $h(t)$ the following result is obtained:
- $$A_i = \frac{A_x}{\Delta t} \cdot \int\limits_{ - \Delta t /2 }^{ + \Delta t /2 } {\rm cos}(2\pi f_i \tau )\hspace{0.1cm}{\rm d}\tau.$$
(4) Approaches 2, 3 and 5 are correct:
- For the direct (DC) signal $x_0(t) = A_x$ , set $f_i = 0$ and one obtains $A_0 = A_x \ \rm \underline{ = \ 1 \hspace{0.05cm} V}$.
- In contrast to this, for the cosine frequencies $f_2 = 2 \ \rm kHz$ and $f_4 = 4 \ \rm kHz$ the integral vanishes in each case because then it is integrated over one and two periods, respectively: $A_2 \ \rm \underline{ = \hspace{0.05cm} 0}$ und $A_4 \hspace{0.05cm} \rm \underline{ = \ 0}$.
- In the frequency domain, the cases which are dealt with here correspond to:
- $$H(f=0) = 1, \hspace{0.3cm}H(f=\Delta f) = 0, \hspace{0.3cm}H(f=2\Delta f) = 0.$$
(5) The result of subtask (3) – considering the symmetry – is for $f_i = f_1$:
- $$A_1= \frac{2A_x}{\Delta t} \cdot \int\limits_{ 0 }^{ \Delta t /2 } {\rm cos}(2\pi f_1 \tau )\hspace{0.1cm}{\rm d}\tau = \frac{2A_x}{2\pi f_1 \cdot \Delta t} \cdot {\rm sin}(2\pi f_1 \frac{\Delta t}{2} )= A_x \cdot {\rm si}(\pi f_1 \Delta t ).$$
- Taking $f_1 · Δt = 0.5$ into account the result is:
- $$A_1 = A_x \cdot {\rm si}(\frac{\pi}{2} ) = \frac{2A_x}{\pi} \hspace{0.15cm}\underline{= 0.637\,{\rm V}}.$$
- Correspondingly, the following is obtained using $f_3 · Δt = 1.5$:
- $$A_3 = A_x \cdot {\rm si}({3\pi}/{2} ) = -\frac{2A_x}{3\pi} = -{A_1}/{3}\hspace{0.15cm}\underline{= -0.212\,{\rm V}}.$$
- The exact same results are obtained – but much faster – by applying the equation:
- $$A_i = A_x · H(f = f_i).$$
- From the graphs on the information page it is already obvious that the integral over $x_1(t)$ is positive in the marked area and the integral over $x_3(t)$ is negative.
- However, it should be noted that in general amplitude is usually referred to as the magnitude (See notice on the information page).