Difference between revisions of "Aufgaben:Exercise 2.10: Shannon-Fano Coding"
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID2465__Inf_A_2_10.png |right|frame|Baumdiagramm der <br> | + | [[File:P_ID2465__Inf_A_2_10.png |right|frame|Baumdiagramm der <br>Shannon-Fano coding]] |
| − | + | Another algorithm for entropy coding was given in 1949 by [https://en.wikipedia.org/wiki/Claude_Shannon Claude Elwood Shannon] and [https://en.wikipedia.org/wiki/Robert_Fano Robert Fano] , which is described in the theory section. | |
| − | + | This special type of source coding will be described here using a simple example for the symbol range $M = 4$ and the following symbol probabilities: | |
:$$p_{\rm A} = 0.2 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.3 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm C}= 0.4 \hspace{0.05cm},\hspace{0.4cm} | :$$p_{\rm A} = 0.2 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.3 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm C}= 0.4 \hspace{0.05cm},\hspace{0.4cm} | ||
p_{\rm D}= 0.1 \hspace{0.05cm}. $$ | p_{\rm D}= 0.1 \hspace{0.05cm}. $$ | ||
| − | + | The graph shows the corresponding tree diagram. Proceed as follows: | |
| − | :1. | + | :1. Order the symbols according to decreasing probability of occurrence, here $\rm C$ – $\rm B$ – $\rm A$ – $\rm D$. |
| − | :2. | + | :2. Divide the symbols into two groups of approximately equal probability, here $\rm C$ and $\rm BAD$. |
| − | :3. | + | :3. The binary symbol <b>0</b>is assigned to the less probable group, <b>1</b> to the other group. |
| − | :4. | + | :4. If there is more than one symbol in a group, the algorithm is to be applied recursively. |
| − | + | For this example, the following code assignment results (in the tree diagram, a red connection marks a <b>1</b> and a blue one a <b>0</b>: | |
: $\rm A$ → <b>111</b>, $\rm B$ → <b>10</b>, $\rm C$ → <b>0</b>, $\rm D$ → <b>110</b>. | : $\rm A$ → <b>111</b>, $\rm B$ → <b>10</b>, $\rm C$ → <b>0</b>, $\rm D$ → <b>110</b>. | ||
| − | + | This gives the following for the mean codeword length: | |
| − | :$$L_{\rm M} = 0.4 \cdot 1 + 0.3 \cdot 2 + (0.2 + 0.1) \cdot 3 = 1.9\,\,{\rm bit/ | + | :$$L_{\rm M} = 0.4 \cdot 1 + 0.3 \cdot 2 + (0.2 + 0.1) \cdot 3 = 1.9\,\,{\rm bit/source\:symbol}\hspace{0.05cm}.$$ |
| − | + | The Huffman algorithm would produce a slightly different code here, but even in this case | |
| − | *$\rm C$ | + | *$\rm C$ is coded with one bit, |
| − | *$\rm B$ | + | *$\rm B$ with two bits and |
| − | *$\rm A$ | + | *$\rm A$ and $\rm D$ with three bits each. |
| − | + | This would also result in $L_{\rm M} = 1.9 \ \rm bit/source\:symbol$. | |
| − | In | + | In this task you are to calculate the Shannon-Fano code for $M = 8$ and the probabilities |
:$$p_{\rm A} = 0.10 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.40 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm C}= 0.02 \hspace{0.05cm},\hspace{0.4cm} p_{\rm D}= 0.14 \hspace{0.05cm},\hspace{0.4cm} | :$$p_{\rm A} = 0.10 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.40 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm C}= 0.02 \hspace{0.05cm},\hspace{0.4cm} p_{\rm D}= 0.14 \hspace{0.05cm},\hspace{0.4cm} | ||
p_{\rm E} = 0.17 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm F}= 0.03 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm G}= 0.05 \hspace{0.05cm},\hspace{0.4cm}p_{\rm H}= 0.09$$ | p_{\rm E} = 0.17 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm F}= 0.03 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm G}= 0.05 \hspace{0.05cm},\hspace{0.4cm}p_{\rm H}= 0.09$$ | ||
| − | + | determine. You will see that with these probabilities "Shannon-Fano" will also differ from "Huffman" in terms of efficiency. | |
| − | + | With the Huffman code, the following assignment results with the probabilities at hand: | |
: $\rm A$ → <b>100</b>, $\rm B$ → <b>0</b>, $\rm C$ → <b>111100</b>, $\rm D$ → <b>101</b>, $\rm E$ → <b>110</b>, $\rm F$ → <b>111101</b>, $\rm G$ → <b>11111</b>, $\rm H$ → <b>1110</b>. | : $\rm A$ → <b>100</b>, $\rm B$ → <b>0</b>, $\rm C$ → <b>111100</b>, $\rm D$ → <b>101</b>, $\rm E$ → <b>110</b>, $\rm F$ → <b>111101</b>, $\rm G$ → <b>11111</b>, $\rm H$ → <b>1110</b>. | ||
| Line 54: | Line 54: | ||
| − | '' | + | ''Hints:'' |
| − | * | + | *The assignment belongs to the chapter [[Information_Theory/Weitere_Quellencodierverfahren|Other source coding methods]]. |
| − | * | + | *In particular, reference is made to the page [[Information_Theory/Weitere_Quellencodierverfahren#The_Shannon-Fano_algorithm|The Shannon-Fano algorithm]]. |
| − | * | + | *To check your results, please refer to the interactive applet [[Applets:Huffman-_und_Shannon-Fano-Codierung|Huffman and Shannon-Fano coding]]. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
Revision as of 12:40, 6 August 2021
Another algorithm for entropy coding was given in 1949 by Claude Elwood Shannon and Robert Fano , which is described in the theory section.
This special type of source coding will be described here using a simple example for the symbol range $M = 4$ and the following symbol probabilities:
- $$p_{\rm A} = 0.2 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.3 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm C}= 0.4 \hspace{0.05cm},\hspace{0.4cm} p_{\rm D}= 0.1 \hspace{0.05cm}. $$
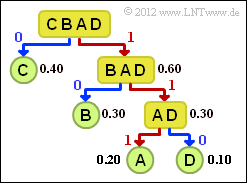
The graph shows the corresponding tree diagram. Proceed as follows:
- 1. Order the symbols according to decreasing probability of occurrence, here $\rm C$ – $\rm B$ – $\rm A$ – $\rm D$.
- 2. Divide the symbols into two groups of approximately equal probability, here $\rm C$ and $\rm BAD$.
- 3. The binary symbol 0is assigned to the less probable group, 1 to the other group.
- 4. If there is more than one symbol in a group, the algorithm is to be applied recursively.
For this example, the following code assignment results (in the tree diagram, a red connection marks a 1 and a blue one a 0:
- $\rm A$ → 111, $\rm B$ → 10, $\rm C$ → 0, $\rm D$ → 110.
This gives the following for the mean codeword length:
- $$L_{\rm M} = 0.4 \cdot 1 + 0.3 \cdot 2 + (0.2 + 0.1) \cdot 3 = 1.9\,\,{\rm bit/source\:symbol}\hspace{0.05cm}.$$
The Huffman algorithm would produce a slightly different code here, but even in this case
- $\rm C$ is coded with one bit,
- $\rm B$ with two bits and
- $\rm A$ and $\rm D$ with three bits each.
This would also result in $L_{\rm M} = 1.9 \ \rm bit/source\:symbol$.
In this task you are to calculate the Shannon-Fano code for $M = 8$ and the probabilities
- $$p_{\rm A} = 0.10 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.40 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm C}= 0.02 \hspace{0.05cm},\hspace{0.4cm} p_{\rm D}= 0.14 \hspace{0.05cm},\hspace{0.4cm} p_{\rm E} = 0.17 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm F}= 0.03 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm G}= 0.05 \hspace{0.05cm},\hspace{0.4cm}p_{\rm H}= 0.09$$
determine. You will see that with these probabilities "Shannon-Fano" will also differ from "Huffman" in terms of efficiency.
With the Huffman code, the following assignment results with the probabilities at hand:
- $\rm A$ → 100, $\rm B$ → 0, $\rm C$ → 111100, $\rm D$ → 101, $\rm E$ → 110, $\rm F$ → 111101, $\rm G$ → 11111, $\rm H$ → 1110.
Hints:
- The assignment belongs to the chapter Other source coding methods.
- In particular, reference is made to the page The Shannon-Fano algorithm.
- To check your results, please refer to the interactive applet Huffman and Shannon-Fano coding.
Questions
Musterlösung
- $$L_{\rm M} = 0.4 \cdot 1 + (0.17 + 0.14 + 0.10) \cdot 3 + 0.09 \cdot 4 + 0.05 \cdot 5 + (0.03 + 0.02) \cdot 6 =\underline{ 2.54 \,\,{\rm bit/Quellensymbol}}\hspace{0.05cm}. $$
(2) Richtig ist die Antwort 2:
- Vor Anwendung des Shannon–Fano–Algorithmus müssen die Zeichen erst nach ihren Auftrittswahrscheinlichkeiten sortiert werden. Damit ist die Antwort 1 falsch.
- Alle sortierten Zeichen müssen so in zwei Gruppen eingeteilt werden, dass die Gruppenwahrscheinlichkeiten möglichst gleich sind. Für den ersten Schritt:
- $${\rm Pr}(\boldsymbol{\rm BE}) = 0.57\hspace{0.05cm}, \hspace{0.2cm}{\rm Pr}(\boldsymbol{\rm DAHGFC}) = 0.43 \hspace{0.05cm}.$$
- Bei der Aufteilung gemäß Lösungsvorschlag 3 würde die Gleichverteilung noch weniger erreicht:
- $${\rm Pr}(\boldsymbol{\rm B}) = 0.40\hspace{0.05cm}, \hspace{0.2cm}{\rm Pr}(\boldsymbol{\rm EDAHGFC}) = 0.60 \hspace{0.05cm}.$$
(3) Alle Lösungsvorschläge sind richtig:
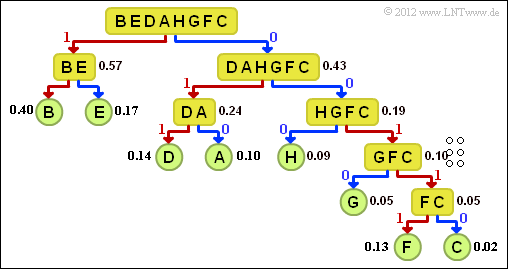
- Die Grafik zeigt das Baumdiagramm der Shannon–Fano–Codierung.
- Daraus ergibt sich folgende Zuordnung (eine rote Verbindung weist auf eine 1 hin, eine blaue auf eine 0):
- $\underline{\rm A}$ → 010, $\underline{\rm B}$ → 11, $\underline{\rm C}$ → 00110,
- ${\rm D}$ → 011, ${\rm E}$ → 10, ${\rm F}$ → 00111, ${\rm G}$ → 0010, ${\rm H}$ → 000.
(4) Mit dem Ergebnis der Teilaufgabe (3) erhält man:
- $$L_{\rm M}= (0.40 + 0.17) \cdot 2 + (0.14 + 0.10 + 0.09) \cdot 3 + 0.05 \cdot 4 + (0.03 + 0.02) \cdot 5 =\underline{ 2.58 \,\,{\rm bit/Quellensymbol}}\hspace{0.05cm}. $$
(5) Richtig sind die Aussagen 2 und 3:
- Im vorliegenden Beispiel ergibt sich bei Shannon–Fano ein ungünstigerer Wert als bei Huffman.
- In den meisten Fällen – so auch im Beispiel auf der Angabenseite – ergibt sich für Huffman und Shannon–Fano ein gleichwertiger Code und damit auch die gleiche mittlere Codewortlänge.
- Einen effektiveren Code als Huffman liefert Shannon–Fano dagegen nie.