Aufgaben:Exercise 2.1Z: Different Signal Courses

• Return to book

Discrete value or continuous value?

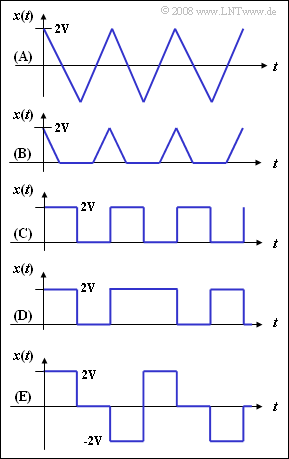
On the right are shown five signals.  The first three signals  $\rm (A)$,  $\rm (B)$  and  $\rm (C)$  are periodic and thus also deterministic, the two lower signals have stochastic character. The current value of these signals  $x(t)$  is taken as a random quantity in each case.

Shown in detail are:

$\rm (A)$:   a triangular-shaped periodic signal,

$\rm (B)$:   the signal  $\rm (A)$  after one-way rectification,

$\rm (C)$:   a rectangular periodic signal,

$\rm (D)$:   a rectangular random signal,

$\rm (E)$:   the random signal  $\rm (D)$  according to  AMI coding;  
          here the "zero" is preserved, while each "one" is alternately encoded with "$+2\hspace{0.03cm}\rm V$" and "$-2\hspace{0.03cm} \rm V$".

Hints:

• The exercise belongs to the chapter  From Random Experiment to Random Variable.

Questions

1

For which signals does the current value describe a discrete random variable?
Consider also the respective number of steps  $M$.

	Signal $\rm (A)$,
	signal $\rm (B)$,
	signal $\rm (C)$,
	signal $\rm (D)$,
	signal $\rm (E)$.

2

For which signals is the current value (exclusively) a continuous random variable?

	signal $\rm (A)$,
	signal $\rm (B)$,
	signal $\rm (C)$,
	signal $\rm (D)$,
	signal $\rm (E)$.

3

Which random variables have a discrete and a continuous part?

	Signal $\rm (A)$,
	signal $\rm (B)$,
	signal $\rm (C)$,
	signal $\rm (D)$,
	signal $\rm (E)$.

4

For the signal  $\rm (D)$  the relative frequency  $h_0$  is determined empirically over $100\hspace{0.03cm}000$ binary symbols.
Name a lower bound for the probability that the determined value lies between  $0.49$  and  $0.51$ ?

${\rm Min\big[\ Pr(0.49}≤h_0≤0.51)\ \big] \ = \ $

5

How many symbols  $(N_\min)$  would you need to use for this investigation to ensure
that the probability for the event "The frequency so determined is between  $0.499$  and  $0.501$" is greater than  $99\%$ ?

$N_\min \ = \ $ $\ \cdot 10^9$

Solution

Solution

(1)  Correct are suggested solutions 3, 4, and 5:

• The random variables  $\rm (C)$  and  $\rm (D)$  are binary  $(M= 2)$,
• whilst the random variable  $\rm (E)$  is trivalent  $(M= 3)$.

(2)  The proposed solution 1 alone is correct:

• The random variable  $\rm (A)$  is continuous in value and can take all values between  $\pm 2 \hspace{0.03cm} \rm V$  with equal probability.
• All other random variables are discrete in value.

(3)  The proposed solution 2 alone is correct:

• Only the random variable  $\rm (B)$  has a discrete part at  $0\hspace{0.03cm}\rm V$, and
• also has a continuous component  (between  $0\hspace{0.03cm} \rm V$  and  $+2\hspace{0.03cm}\rm V)$.

(4)  According to Bernoulli's law of large numbers:

$$\rm Pr\left(|\it h_{\rm 0} - \it p_{\rm 0}|\ge\it\varepsilon\right)\le\frac{\rm 1}{\rm 4\cdot \it N\cdot\it\varepsilon^{\rm 2}} = {\it p}_{\rm \hspace{0.01cm}Bernouilli}.$$

• Thus, the probability that the relative frequency $h_0$ deviates from the probability $p_0 = 0.5$ by more than $0.01$ can be calculated as $\varepsilon = 0.01$:

$${\it p}_{\rm \hspace{0.01cm}Bernoulli} = \rm\frac{1}{4\cdot 100000\cdot 0.01^2}=\rm 2.5\% \hspace{0.5cm}\Rightarrow \hspace{0.5cm} {\rm Min}\big[({\rm Pr}(0.49 \le h_0 \le 0.51)\big] \hspace{0.15cm}\underline{= 0.975}.$$

(5)  With  $p_{\rm Bernoulli} = 1 - 0.99 = 0.01$  and  $\varepsilon = 0.001$  holds again by the law of large numbers:

$${\it p}_{\rm \hspace{0.01cm}Bernoulli}\le\frac{\rm 1}{\rm 4\cdot \it N\cdot\it \varepsilon^{\rm 2}}.$$

• Solved for  $N$ , one gets:

$$N\ge\frac{\rm 1}{\rm 4\cdot\it p_{\rm \hspace{0.01cm}Bernoulli}\cdot\varepsilon^{\rm 2}}=\rm \frac{1}{4\cdot 0.01\cdot 0.001^{2}}=\rm 0.25\cdot 10^8 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} {\it N}_{\rm min} \hspace{0.15cm}\underline{= 2.5\cdot 10^9}.$$