Difference between revisions of "Aufgaben:Exercise 3.1Z: Hilbert Transform"
| Line 3: | Line 3: | ||
}} | }} | ||
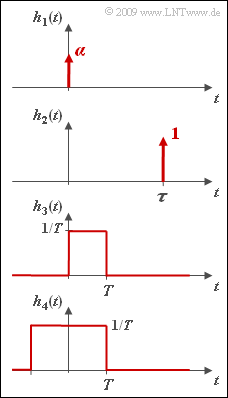
| − | [[File:P_ID1756__LZI_Z_3_1.png|right|frame| | + | [[File:P_ID1756__LZI_Z_3_1.png|right|frame|Considered impulse responses]] |
| − | + | The relation between the real and the imaginary part of the transfer function of realizable causal systems is described by the Hilbert transformation. Here, the following holds: | |
:$${\rm Im} \left\{ H(f) \right \} = - \frac{1}{\pi }\int_{-\infty}^{ | :$${\rm Im} \left\{ H(f) \right \} = - \frac{1}{\pi }\int_{-\infty}^{ | ||
+\infty} | +\infty} | ||
| Line 14: | Line 14: | ||
d}\nu \hspace{0.05cm}.$$ | d}\nu \hspace{0.05cm}.$$ | ||
| − | + | The following is used as a common abbreviation for these two integral transformations: | |
:$${\rm Im} \left\{ H(f) \right \} \quad | :$${\rm Im} \left\{ H(f) \right \} \quad | ||
\bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad | \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad | ||
{\rm Re} \left\{ H(f) \right \}\hspace{0.05cm}.$$ | {\rm Re} \left\{ H(f) \right \}\hspace{0.05cm}.$$ | ||
| − | + | Since the transformation and its inverse differ only by the sign, one equation is sufficient. Here, the following applies: | |
| − | * | + | * To compute the operand marked by the arrow the positive sign is used. |
| − | * | + | * In contrast to this, the minus sign is taken into account for the computation of the operand marked by the circle. |
| − | + | The Hilbert transformation pertains much more generally than only to the case of application described here. For example, it is also used to determine the (complex) analytical signal corresponding to a real band-pass signal. | |
| − | + | In this exercise, the corresponding frequency responses $H(f)$ are to be determined for the causal impulse responses $h(t)$ given in the diagram according to the inverse Fourier transformation. | |
| − | + | If $H(f)$ is decomposed into in real and imaginary parts respectively, then Hilbert correspondences can be derived from it. | |
| Line 49: | Line 49: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Determine the Hilbert transform of a constant $\alpha$ starting from $h_1(t) = \alpha \cdot \delta(t)$ . <br>Which statements are true? |
|type="()"} | |type="()"} | ||
| − | - | + | - The Hilbert transform of a constant $\alpha$ is also $\alpha$. |
| − | + | + | + The Hilbert transform of a constant $\alpha$ is zero. |
| − | - | + | - The Hilbert transform of a constant $\alpha$ is sinusoidal. |
| − | { | + | {Determine the the Hilbert transform of a cosine function starting from $h_2(t) = \delta(t- \tau)$ . <br>Which statements are true? |
|type="()"} | |type="()"} | ||
- Die Hilbert–Transformierte von einem Cosinus ist eine Konstante. | - Die Hilbert–Transformierte von einem Cosinus ist eine Konstante. | ||
Revision as of 10:04, 24 September 2021
The relation between the real and the imaginary part of the transfer function of realizable causal systems is described by the Hilbert transformation. Here, the following holds:
- $${\rm Im} \left\{ H(f) \right \} = - \frac{1}{\pi }\int_{-\infty}^{ +\infty} { \frac{{\rm Re} \left\{ H(\nu) \right \}}{f - \nu}}\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm},$$
- $${\rm Re} \left\{ H(f) \right \} = \frac{1}{\pi }\int_{-\infty}^{ +\infty} { \frac{{\rm Im} \left\{ H(\nu) \right \}}{f - \nu}}\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$
The following is used as a common abbreviation for these two integral transformations:
- $${\rm Im} \left\{ H(f) \right \} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad {\rm Re} \left\{ H(f) \right \}\hspace{0.05cm}.$$
Since the transformation and its inverse differ only by the sign, one equation is sufficient. Here, the following applies:
- To compute the operand marked by the arrow the positive sign is used.
- In contrast to this, the minus sign is taken into account for the computation of the operand marked by the circle.
The Hilbert transformation pertains much more generally than only to the case of application described here. For example, it is also used to determine the (complex) analytical signal corresponding to a real band-pass signal.
In this exercise, the corresponding frequency responses $H(f)$ are to be determined for the causal impulse responses $h(t)$ given in the diagram according to the inverse Fourier transformation.
If $H(f)$ is decomposed into in real and imaginary parts respectively, then Hilbert correspondences can be derived from it.
Please note:
- The exercise belongs to the chapter Conclusions from the Allocation Theorem.
- In particular, reference is made to the theory page Hilbert transformation.
Questions
Solution
- Die Fourier–Transformierte von $h_1(t) = \alpha \cdot \delta(t)$ lautet:
- $$H_1(f) = \alpha \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Re} \left\{ H_1(f) \right \} = \alpha , \hspace{0.2cm}{\rm Im} \left\{ H_1(f) \right \} = 0\hspace{0.05cm}.$$
(2) Richtig ist der letzte Lösungsvorschlag:
- Mit dem Verschiebungssatz und dem Satz von Euler erhält man für die Impulsantwort $h_2(t)$ den Frequenzgang:
- $$H_2(f) ={\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f \tau} = \cos (2\pi f \tau) - {\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \sin (2\pi f \tau)\hspace{0.05cm}.$$
- Daraus ergibt sich die Hilbert–Korrespondenz
- $$\cos (2\pi f \tau) \hspace{0.3cm} \leftarrow\hspace{-0.05cm}\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.3cm} -\sin (2\pi f \tau)\hspace{0.7cm}{\rm oder}\hspace{0.7cm} \cos (2\pi f \tau) \hspace{0.3cm} \bullet\hspace{-0.05cm}\!\!-\!\!\!-\!\!\!-\!-\!\hspace{-0.1cm}\rightarrow\hspace{0.3cm} \sin (2\pi f \tau) \hspace{0.05cm}.$$
(3) Richtig sind beide Lösungsvorschläge:
- Für die rechteckförmige Impulsantwort $h_3(t)$ mit Breite $T$ und Höhe $1/T$ erhält man die Spektralfunktion gemäß dem ersten Fourierintegral:
- $$H_3(f) = \int_{-\infty}^{ +\infty} { h_3(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f t}}\hspace{0.1cm}{\rm d}t \hspace{0.05cm} = \frac{1}{T} \cdot \int_{0}^{ T} { {\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f t}}\hspace{0.1cm}{\rm d}t = \left [\frac{1}{-{\rm j}\cdot 2\pi f T} \cdot {\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f\hspace{0.05cm} t} \right ]_{0}^{T} = \frac{1-{\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f\hspace{0.05cm} T}}{{\rm j}\cdot 2\pi f T} \hspace{0.05cm}.$$
- Mit dem Eulerschen Satz kann hierfür auch geschrieben werden:
- $$H_3(f) = \frac{1-\cos (2\pi f T) + {\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \sin (2\pi f T)}{{\rm j}\cdot 2\pi f T} = \frac{\sin (2\pi f T)}{ 2\pi f T} - {\rm j}\cdot \frac{1 - \cos (2\pi f T)}{ 2\pi f T}\hspace{0.05cm}.$$
- Weiter gilt mit der Umformung $1 - \cos(\alpha) = 2 \cdot \sin^2(\alpha/2)$:
- $${\rm Re}\hspace{-0.05cm} \left\{ H_3(f) \right \} = {\rm si} (2\pi f T)\hspace{0.2cm}{\rm mit}\hspace{0.2cm}{\rm si}(x)= {\rm sin}(x)/x \hspace{0.05cm}, \hspace{0.5cm} {\rm Im} \hspace{-0.05cm}\left\{ H_3(f) \right \} = -\frac{\sin^2 (\pi f T)}{ \pi f T}= - {\rm si} (\pi f T) \cdot {\rm sin} (\pi f T) \hspace{0.05cm}.$$
(4) Richtig ist Nein:
- Die Impulsantwort $h_4(t)$ ist nicht kausal, so dass aus dem dazugehörigen Fourier–Spektrum $H_4(f)$ keine Hilbert–Korrespondenz abgeleitet werden kann.