Difference between revisions of "Aufgaben:Exercise 3.3Z: Characteristics Determination"
m (→Solution) |
m |
||
| Line 87: | Line 87: | ||
'''(5)''' The given equation can be rewritten as follows: | '''(5)''' The given equation can be rewritten as follows: | ||
:$$\eta = \frac{2 \cdot {\rm J}_{1}{(\eta)}}{{\rm J}_{0}(\eta) + {\rm J}_{2}(\eta)} \hspace{0.05cm}.$$ | :$$\eta = \frac{2 \cdot {\rm J}_{1}{(\eta)}}{{\rm J}_{0}(\eta) + {\rm J}_{2}(\eta)} \hspace{0.05cm}.$$ | ||
| − | * | + | *With ${\rm J}_0(η) = 0.512$, ${\rm J}_1(η) = 0.558$ and ${\rm J}_2(η) = 0.232$ we thus get: |
:$$ \eta = \frac{2 \cdot 0.558}{0.512 + 0.232}\hspace{0.15cm}\underline { = 1.5}\hspace{0.05cm}.$$ | :$$ \eta = \frac{2 \cdot 0.558}{0.512 + 0.232}\hspace{0.15cm}\underline { = 1.5}\hspace{0.05cm}.$$ | ||
Latest revision as of 17:03, 9 April 2022
Let us consider the phase modulation of the harmonic oscillation
- $$q(t) = A_{\rm N} \cdot \cos(2 \pi \cdot f_{\rm N} \cdot t + \phi_{\rm N}) \hspace{0.05cm},$$
which, given a normalized carrier amplitude $(A_{\rm T} = 1)$ , leads to the following transmitted signal:
- $$ s(t) = \cos \hspace{-0.1cm}\big[\omega_{\rm T} \cdot t + K_{\rm PM} \cdot q(t) \big]\hspace{0.05cm}.$$
The spectrum of the corresponding analytical signal $s_{\rm TP}(t)$ is generally:
- $$S_{\rm TP}(f) = \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n\hspace{0.05cm}\cdot \hspace{0.05cm}(\phi_{\rm N}\hspace{0.05cm}+\hspace{0.05cm} 90^\circ) }\cdot \hspace{0.05cm} \delta (f - n \cdot f_{\rm N})\hspace{0.05cm}$$
Here, $η = K_{\rm PM} · A_{\rm N}$ is called the modulation index.
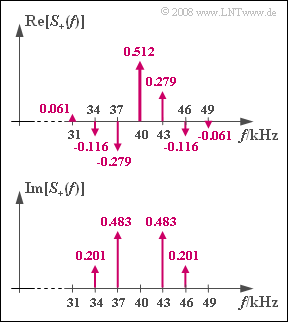
In the graph, the real and imaginary parts of the spectrum $S_+(f)$ of the analytical signal $s_+(t)$ are shown separately. This should be used to determine the characteristics $f_{\rm T}$, $f_{\rm N}$, $ϕ_{\rm N}$ and $η$ .
Hints:
- This exercise belongs to the chapter Phase Modulation.
- Particular reference is made to the page Equivalent low-pass signal in phase modulation.
- For the calculation of the modulation index, you can take advantage of the following property of the Bessel function:
- $${\rm J}_n (\eta) = \frac{2 \cdot (n-1)}{\eta} \cdot {\rm J}_{n-1} (\eta) - {\rm J}_{n-2} (\eta) \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm J}_{2} (\eta)= {2}/{\eta} \cdot {\rm J}_{1} (\eta) - {\rm J}_{0} (\eta) \hspace{0.05cm}.$$
Questions
Solution
(2) Considering $S_{\rm TP}(f = 3{\ \rm kHz}) = S_+(f = 43 \ \rm kHz)$ , it holds that:
- $$|S_{\rm TP}(f = 3\,{\rm kHz})| = \sqrt{0.279^2 + 0.483^2} \hspace{0.15cm}\underline {= 0.558}\hspace{0.05cm},$$
- $$ {\rm arc}\hspace{0.15cm} S_{\rm TP}(f = 3\,{\rm kHz}) = \arctan \frac{0.483}{0.279} = \arctan 1.732\hspace{0.15cm}\underline { = 60^\circ} \hspace{0.05cm}.$$
(3) Analogously to in question (2) , at frequency $f = 6 \ \rm kHz$ we obtain:
- $$|S_{\rm TP}(f = 6\,{\rm kHz})| = \sqrt{(-0.116)^2 + 0.201^2} \hspace{0.15cm}\underline {= 0.232}\hspace{0.05cm},$$
- $${\rm arc}\hspace{0.15cm} S_{\rm TP}(f = 6\,{\rm kHz}) = \arctan \frac{-0.116}{0.201} = 180^\circ - \arctan 1.732 \hspace{0.15cm}\underline {= 120^\circ} \hspace{0.05cm}.$$
(4) When $n = 1$ ⇒ $f = 3 \ \rm kHz$ as in question (2), the phase is:
- $$ \phi_{\rm N} + 90^\circ = 60^\circ \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\phi_{\rm N} = -30^\circ\hspace{0.05cm}.$$
- Checking this result when $n = 2$ ⇒ $f = 6 \ \rm kHz$ as in question (3) yields the same value:
- $$ 2\cdot (\phi_{\rm N} + 90^\circ) = 120^\circ \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\phi_{\rm N} \hspace{0.15cm}\underline {= -30^\circ}\hspace{0.05cm}.$$
(5) The given equation can be rewritten as follows:
- $$\eta = \frac{2 \cdot {\rm J}_{1}{(\eta)}}{{\rm J}_{0}(\eta) + {\rm J}_{2}(\eta)} \hspace{0.05cm}.$$
- With ${\rm J}_0(η) = 0.512$, ${\rm J}_1(η) = 0.558$ and ${\rm J}_2(η) = 0.232$ we thus get:
- $$ \eta = \frac{2 \cdot 0.558}{0.512 + 0.232}\hspace{0.15cm}\underline { = 1.5}\hspace{0.05cm}.$$