Exercise 4.06Z: Signal Space Constellations

Three signal space constellations

The (mean) error probability of an optimal binary system is:

$$p_{\rm S} = {\rm Pr}({ \cal E} ) = {\rm Q} \left ( \frac{d/2}{\sigma_n} \right )\hspace{0.05cm}.$$

It should be noted here:

${\rm Q}(x)$ denotes the complementary Gaussian error function (definition and approximation):

$${\rm Q}(x) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{\sqrt{2\pi}} \int_{x}^{\infty} {\rm e}^{-u^2/2} \,{\rm d} u \approx \frac{1}{\sqrt{2\pi} \cdot x} \cdot {\rm e}^{-x^2/2} \hspace{0.05cm}.$$

$d$ specifies the distance between the two transmitted signal points $s_0$ and $s_1$ in vector space:

$$d = \sqrt{ || \boldsymbol{ s }_1 - \boldsymbol{ s }_0||^2} \hspace{0.05cm}.$$

$\sigma_n^2$ is the variance of the AWGN noise after the detector, which, for example, can be implemented as a matched filter.
It is assumed that $\sigma_n^2 = N_0/2$.

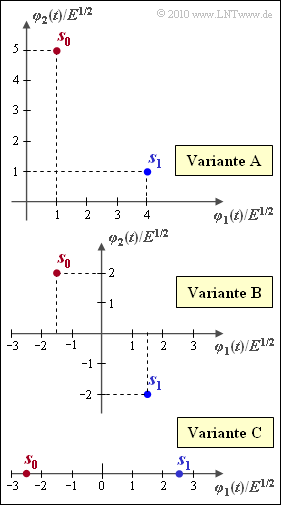
The graphic shows three different signal space constellations, namely

Variant $\rm A$: $s_0 = (+1, \, +5), \hspace{0.4cm} s_1 = (+4, \, +1)$,
Variant $\rm B$: $s_0 = (-1.5, \, +2), \, s_1 = (+1.5, \, -2)$,
Variant $\rm C$: $s_0 = (-2.5, \, 0), \hspace{0.45cm} s_1 = (+2.5, \, 0)$.

The mean energy per symbol $(E_{\rm S})$ can be calculated as follows:

$$E_{\rm S} = {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_0) \cdot || \boldsymbol{ s }_0||^2 + {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_1) \cdot || \boldsymbol{ s }_1||^2\hspace{0.05cm}.$$

Notes:

The chapter belongs to the chapter "Approximation of the Error Probability".
For numeric calculations, the energy $E = 1$ can be set for simplification.
Unless otherwise specified, equally probable symbols can be assumed:

$${\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_0) = {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_1) = 0.5\hspace{0.05cm}.$$

Questions

	Additive white Gaussian noise with variance $\sigma_n^2$.
	Optimal binary receiver.
	Decision boundary in the middle between the symbols.
	Equally likely symbols $s_0$ and $s_1$.

	Variant $\rm A$ has the lowest error probability.
	Variant $\rm B$ has the lowest error probability.
	Variant $\rm C$ has the lowest error probability.
	All variants show the same error behavior.

$p_{\rm S} \ = \ $

$\ \%$

$p_{\rm S} \ = \ $

$\ \%$

$p_{\rm S} \ = \ $

$\ \%$

$E_{\rm S} \ = \ $

$\ \cdot 10^{\rm –6} \ \rm Ws$

Solution

(1) The first three prerequisites must be met in any case:

The equation then applies independently of the occurrence probabilities.
In the case of ${\rm Pr}(\boldsymbol{s} = \boldsymbol{s}_0) ≠ {\rm Pr}(\boldsymbol{s} = \boldsymbol{s}_1)$, a lower error probability can be achieved by shifting the decision threshold.

(2) The noise rms value $\sigma_n$ and thus also the signal energy $E = \sigma_n^2$ are the same for all three considered variants. The same applies to the distance of the signal space points. For variant $\rm A$, for example, the following applies:

$$d = \sqrt{ || \boldsymbol{ s }_1 - \boldsymbol{ s }_0||^2} = \sqrt{ E \cdot (4-1)^2 + E \cdot (1-5)^2} = 5 \cdot \sqrt{E}\hspace{0.05cm}.$$

Due to the shifting of the coordinate system, the distance between $\boldsymbol{s}_0$ and $\boldsymbol{s}_1$ does not change (variant $\rm B$), and the same distance results in variant $\rm C$ (after rotation).

Solution 4 is correct:

By rotating the coordinate system, one can always get by with a basis function $(N = 1)$ for a binary system $(M = 2)$.
Since the two-dimensional noise is circularly symmetric ⇒ equal standard deviation $\sigma_n$ in all directions, the noise term can also be described one-dimensionally as in the chapter "Error Probability for Baseband Transmission".

(3) For all variants considered here, i.e., also for variant $\rm A$, the following holds:

$$p_{\rm S} = {\rm Pr}({ \cal E} ) = {\rm Q} \left ( \frac{d/2}{\sigma_n} \right )= {\rm Q} \left ( \frac{5/2 \cdot \sqrt{E}}{\sigma_n} \right ) = {\rm Q}(2.5)\hspace{0.05cm}.$$

With the given approximation we obtain

$$p_{\rm S} = \frac{1}{\sqrt{2\pi} \cdot 2.5} \cdot {\rm e}^{-2.5^2/2} \hspace{0.1cm} \hspace{0.15cm}\underline {\approx 0.7 \%}\hspace{0.05cm}.$$

(4) For variant $\rm C$, the average energy per symbol is given by:

$$E_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_0) \cdot (-2.5 \cdot \sqrt{E})^2 + {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_1) \cdot (+ 2.5 \cdot \sqrt{E})^2 = \left [ {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_0) + {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_0) \right ] \cdot 6.25 \cdot E = 6.25 \cdot E$$

$$\Rightarrow \hspace{0.3cm} E = \frac {E_{\rm S}}{6.25} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \sqrt{E}= \frac {\sqrt{E_{\rm S}}}{2.5} \hspace{0.05cm}.$$

Substituting this result into the equation found in (3), we obtain with $\sigma_n^2 = N_0/2$:

$$p_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Q} \left ( \frac{2.5 \cdot \sqrt{E}}{\sigma_n} \right )= {\rm Q} \left ( \frac{ \sqrt{E_{\rm S}}}{\sigma_n} \right ) = {\rm Q} \left ( \frac{ \sqrt{2 \cdot E_{\rm S}}}{N_0} \right ) ={\rm Q} \left ( \sqrt{\frac{ 2 \cdot 6.25 \cdot 10^{-6}\,{\rm Ws}}{2 \cdot 10^{-6}\,{\rm W/Hz}}} \right ) ={\rm Q}(2.5) \hspace{0.1cm} \hspace{0.15cm}\underline {\approx 0.7 \%}\hspace{0.05cm}. $$

(5) Rotating the coordinate system does not change the energy ratios. Therefore, $p_{\rm S} \ \underline {\approx 0.7\%}$ is obtained again.

(6) In variant $\rm A$, the average energy per symbol is

$$E_{\rm S} = {1}/{2} \cdot \left [ (1^2 + 5^2) \cdot E + (4^2 + 1^2) \cdot E \right ] = 21.5 \cdot E \hspace{0.05cm}. $$

The distance from the threshold, which should be midway between $\boldsymbol{s}_0$ and $\boldsymbol{s}_1$ for equally probable symbols, is $d/2 = 2.5 \cdot E^{\rm 1/2}$, as in the other variants. Thus, with $\sigma_n^2 = N_0/2$, we obtain the governing equation:

$$p_{\rm S} = {\rm Q} \left ( \frac{ 2.5 \cdot \sqrt{E}}{\sqrt{N_0/2}} \right ) ={\rm Q}(2.5)\approx 0.7 \cdot 10^{-2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \sqrt{\frac {2E}{N_0}} = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \frac {E}{N_0} = 0.5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\frac {E_{\rm S}}{21.5 \cdot N_0} = 0.5$$

$$\Rightarrow \hspace{0.3cm} {E_{\rm S}} = 0.5 \cdot {21.5 \cdot N_0} \hspace{0.1cm} \hspace{0.15cm}\underline { = 21.5 \cdot 10^{-6}\,{\rm Ws}}\hspace{0.05cm}.$$

This means: For variant $\rm A$, compared to the other two symbols, a mean symbol energy $E_{\rm S}$ larger by a factor of $3.44$is required to achieve the same error probability $p_{\rm S} = 0.7%$.

That means: This signal space constellation is very unfavorable. It results in a very large $E_{\rm S}$ without increasing the distance $d$ at the same time.
With $E_{\rm S} = 6.25 \cdot 10^{\rm –6} \ \rm Ws$, on the other hand, $p_{\rm S} = {\rm Q}(2.5/3.44^{\rm 1/2}) \approx {\rm Q}(1.35) \approx 9\%$ would result.
That means: The error probability would be larger by more than one power of ten.