Difference between revisions of "Aufgaben:Exercise 4.2Z: Eight-level Phase Shift Keying"
| Line 57: | Line 57: | ||
- $\varphi_1(t) = g_s(t)$, | - $\varphi_1(t) = g_s(t)$, | ||
+ $\varphi_1(t) = g_s(t)/E_{\rm gs}^{\rm 0.5}$, | + $\varphi_1(t) = g_s(t)/E_{\rm gs}^{\rm 0.5}$, | ||
| − | + $\ | + | + $\psi_1(t) = \varphi_1(t)$, |
| − | - $\ | + | - $\psi_1(t) = j \cdot \varphi_1(t)$. |
{Es gelte $s_{\rm TP0}(t) = E^{\rm 0.5}$. Was trifft zu: | {Es gelte $s_{\rm TP0}(t) = E^{\rm 0.5}$. Was trifft zu: | ||
Revision as of 13:10, 6 November 2017
Die $M = 8$ möglichen Sendesignale bei 8–PSK lauten mit $i = 0, \ ... \ , 7$ im Bereich $0 ≤ t < T$:
- $$s_i(t)= A \cdot \cos(2\pi f_{\rm T}t + i \cdot {\pi}/{4}) \hspace{0.05cm}.$$
Außerhalb der Symboldauer $T$ sind die Signale $s_i(t)$ alle gleich $0$.
In der Aufgabe A4.2 wurde gezeigt, dass diese Signalmenge durch die Basisfunktionen
- $$\varphi_1(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t )\hspace{0.05cm},$$
- $$\varphi_2(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} - \sqrt{{2}/{T}} \cdot \sin(2\pi f_{\rm T}t )\hspace{0.05cm}$$
wie folgt dargestellt werden kann ($i = 0, \ ... \ , 7$):
- $$s_i(t)= s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) \hspace{0.05cm}.$$
Die äquivalente Tiefpassdarstellung der Signale $s_i(t)$ lautet nach dem Blockschaltbild in Kapitel 4.3 des Buches „Modulationsverfahren”:
- $$s_{{\rm TP}i}(t)= a_{i} \cdot g_s(t) \hspace{0.05cm}, \hspace{0.2cm}a_{i} = a_{{\rm I}i} + {\rm j} \cdot a_{{\rm Q}i} \hspace{0.05cm}, \hspace{0.2cm}i = 0, ... \hspace{0.1cm} , 7 \hspace{0.05cm},$$
wobei $a_i$ komplexe dimensionslose Koeffizienten sind und die Energie des Sendegrundimpulses $g_s(t)$ im Tiefpassbereich $E_{\it gs}$ beträgt. Im hier dargestellten Fall beschreibt $g_s(t)$ einen Rechteckimpuls, doch kann für $g_s(t)$ auch ein jeder andere energiebegrenzte Impuls verwendet werden.
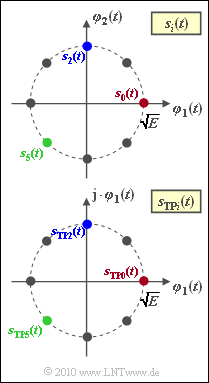
Die Grafik zeigt die Signalraumdarstellung der 8–PSK für das Bandpass–Signal (oben) sowie für das äquivalente Tiefpass–Signal (unten). Man erkennt daraus, dass sich die beiden Darstellungen nur duch die verwendeten Basisfunktionen unterscheiden, wobei $\varphi_1(t)$ in der oberen und der unteren Grafik für unterschiedliche Funktionen steht. In der Tiefpassdarstellung gilt $\varphi_2(t) = j \cdot \varphi_1(t)$.
Hinweise:
- Die Aufgabe gehört zum Themengebiet von Kapitel Signale, Basisfunktionen und Vektorräume.
- Im Gegensatz zum Theorieteil und zur Aufgabe A4.2 kann hier die Laufvariable $i$ die Werte $0, \ ... \, M–1$ annehmen. Verwenden Sie zur Abkürzung
- $$E = {A^2 \cdot T}/{2}\hspace{0.05cm}.$$
Fragebogen
Musterlösung