Difference between revisions of "Aufgaben:Exercise 4.9Z: Is Channel Capacity C ≡ 1 possible with BPSK?"
| Line 3: | Line 3: | ||
}} | }} | ||
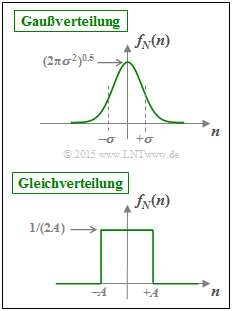
| − | [[File:P_ID2947__Inf_Z_4_9.png|right|frame|WDF <i>f<sub>N</sub></i>(<i>n</i>) | + | [[File:P_ID2947__Inf_Z_4_9.png|right|frame|Zwei unterschiedliche Störkomponenten mit WDF <i>f<sub>N</sub></i>(<i>n</i>)]] |
Wir gehen hier von einem binären bipolaren Quellensignal aus ⇒ <i>X</i> = (+1, –1). Die Wahrscheinlichkeitsdichtefunktion (WDF) der Quelle lautet somit: | Wir gehen hier von einem binären bipolaren Quellensignal aus ⇒ <i>X</i> = (+1, –1). Die Wahrscheinlichkeitsdichtefunktion (WDF) der Quelle lautet somit: | ||
| Line 72: | Line 72: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' Die differentielle Entropie einer Gleichverteilung der absoluten Breite 2<i>A</i> ist gleich | '''(1)''' Die differentielle Entropie einer Gleichverteilung der absoluten Breite 2<i>A</i> ist gleich | ||
| − | $$ h(N) = {\rm log}_2 \hspace{0.1cm} (2A) | + | :$$ h(N) = {\rm log}_2 \hspace{0.1cm} (2A) |
\hspace{0.3cm}\Rightarrow \hspace{0.3cm} A=1/8\hspace{-0.05cm}: | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} A=1/8\hspace{-0.05cm}: | ||
\hspace{0.15cm}h(N) = {\rm log}_2 \hspace{0.1cm} (1/4) | \hspace{0.15cm}h(N) = {\rm log}_2 \hspace{0.1cm} (1/4) | ||
\hspace{0.15cm}\underline{= -2\,{\rm bit(/Symbol)}}\hspace{0.05cm}.$$ | \hspace{0.15cm}\underline{= -2\,{\rm bit(/Symbol)}}\hspace{0.05cm}.$$ | ||
| + | |||
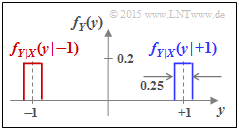
| + | [[File:P_ID2948__Inf_Z_4_9b.png|right|frame|WDF der Ausgangsgröße <i>Y</i> bei gleichverteilter Störung <i>N</i>]] | ||
'''(2)''' Die Wahrscheinlichkeitsdichtefunktion am Ausgang ergibt sich entsprechend der Gleichung: | '''(2)''' Die Wahrscheinlichkeitsdichtefunktion am Ausgang ergibt sich entsprechend der Gleichung: | ||
| − | + | :$$f_Y(y) = {1}/{2} \cdot \left [ f_{Y|{X}}(y|-1) + f_{Y|{X}}(y|+1) \right ]\hspace{0.05cm}.$$ | |
| − | $$f_Y(y) = {1}/{2} \cdot \left [ f_{Y|{X}}(y|-1) + f_{Y|{X}}(y|+1) \right ]\hspace{0.05cm}.$$ | ||
Die Grafik zeigt das Ergebnis für unser Beispiel (<i>A</i> = 1/8): | Die Grafik zeigt das Ergebnis für unser Beispiel (<i>A</i> = 1/8): | ||
| − | + | * Rot gezeichnet ist der erste Term 1/2 · <i>f<sub>Y|X</sub></i>(<i>y</i>|–1), wobei das Rechteck <i>f<sub>N</sub></i>(<i>n</i>) an die Stelle <i>Y</i> = –1 verschoben und mit 1/2 multipliziert wird. Es ergibt sich ein Rechteck der Breite 2<i>A</i> = 1/4 und der Höhe 1/(4<i>A</i>) = 2. | |
| − | + | * Blau dargestellt ist der zweite Term 1/2 · <i>f<sub>Y|X</sub></i>(<i>y</i>|+1) mit der Mitte bei <i>Y</i> = +1. | |
| − | + | * Lässt man die Farben außer Betracht, so ergibt sich die gesamte WDF <i>f<sub>Y</sub></i>(<i>y</i>). | |
Die differentiellen Entropie wird nicht verändert wird, wenn man nicht überlappende WDF–Abschnitte verschiebt. Somit ergibt sich für die gesuchte differentielle Sinkenentropie: | Die differentiellen Entropie wird nicht verändert wird, wenn man nicht überlappende WDF–Abschnitte verschiebt. Somit ergibt sich für die gesuchte differentielle Sinkenentropie: | ||
| − | $$h(Y) = {\rm log}_2 \hspace{0.1cm} (4A) | + | :$$h(Y) = {\rm log}_2 \hspace{0.1cm} (4A) |
\hspace{0.3cm}\Rightarrow \hspace{0.3cm} A=1/8\hspace{-0.05cm}: | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} A=1/8\hspace{-0.05cm}: | ||
\hspace{0.15cm}h(Y) = {\rm log}_2 \hspace{0.1cm} (1/2) | \hspace{0.15cm}h(Y) = {\rm log}_2 \hspace{0.1cm} (1/2) | ||
| − | \hspace{0.15cm}\underline{= -1\,{\rm bit(/Symbol)}}\hspace{0.05cm}.$$ | + | \hspace{0.15cm}\underline{= -1\,{\rm bit(/Symbol)}}\hspace{0.05cm}.$$ |
| + | |||
'''(3)''' Damit erhält man für die Transinformation zwischen Quelle und Sinke: | '''(3)''' Damit erhält man für die Transinformation zwischen Quelle und Sinke: | ||
| − | $$I(X; Y) = h(Y) \hspace{-0.05cm}-\hspace{-0.05cm} h(N) = (-1\,{\rm bit/Symbol})\hspace{-0.05cm} -\hspace{-0.05cm}(-2\,{\rm bit/Symbol}) | + | :$$I(X; Y) = h(Y) \hspace{-0.05cm}-\hspace{-0.05cm} h(N) = (-1\,{\rm bit/Symbol})\hspace{-0.05cm} -\hspace{-0.05cm}(-2\,{\rm bit/Symbol}) |
\hspace{0.15cm}\underline{= +1\,{\rm bit/Symbol}}\hspace{0.05cm}.$$ | \hspace{0.15cm}\underline{= +1\,{\rm bit/Symbol}}\hspace{0.05cm}.$$ | ||
| + | |||
'''(4)''' <u>Alle Lösungsvorschläge</u> sind zutreffend: | '''(4)''' <u>Alle Lösungsvorschläge</u> sind zutreffend: | ||
| − | + | * Für jedes <i>A</i> ≤ 1 gilt | |
| − | $$ h(Y) = {\rm log}_2 \hspace{0.1cm} (4A) = {\rm log}_2 \hspace{0.1cm} (2A) + {\rm log}_2 \hspace{0.1cm} (2)\hspace{0.05cm}, | + | :$$ h(Y) = {\rm log}_2 \hspace{0.1cm} (4A) = {\rm log}_2 \hspace{0.1cm} (2A) + {\rm log}_2 \hspace{0.1cm} (2)\hspace{0.05cm}, \hspace{0.5cm} |
| − | + | h(N) = {\rm log}_2 \hspace{0.1cm} (2A)$$ | |
| − | $$\Rightarrow \hspace{0.3cm} I(X; Y) = h(Y) \hspace{-0.05cm}- \hspace{-0.05cm}h(N) = {\rm log}_2 \hspace{0.1cm} (2) | + | :$$\Rightarrow \hspace{0.3cm} I(X; Y) = h(Y) \hspace{-0.05cm}- \hspace{-0.05cm}h(N) = {\rm log}_2 \hspace{0.1cm} (2) |
\hspace{0.15cm}\underline{= +1\,{\rm bit/Symbol}}\hspace{0.05cm}.$$ | \hspace{0.15cm}\underline{= +1\,{\rm bit/Symbol}}\hspace{0.05cm}.$$ | ||
| − | + | * An diesem Prinzip ändert sich auch bei anderer WDF <i>f<sub>N</sub></i>(<i>n</i>) nichts, solange die Störung auf den Bereich |<i>n</i>| ≤ 1 begrenzt ist. | |
| − | + | * Überlappen sich jedoch die beiden bedingten Wahrscheinlichkeitsdichtefunktionen, so ergibt sich für <i>h</i>(<i>Y</i>) ein kleinerer Wert als oben berechnet und damit auch eine kleinere Transinformation. | |
| − | [[File:P_ID2951__Inf_Z_4_9e.png|right|]] | + | |
| + | |||
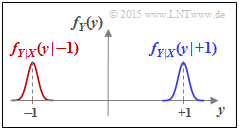
| + | [[File:P_ID2951__Inf_Z_4_9e.png|right|frame|WDF der Ausgangsgröße <i>Y</i> bei gaußverteilter Störung <i>N</i>]] | ||
'''(5)''' Richtig ist der <u>Lösungsvorschlag 2</u>: | '''(5)''' Richtig ist der <u>Lösungsvorschlag 2</u>: | ||
| − | + | * Die Gaußfunktion klingt zwar sehr schnell ab, sie wird aber nie exakt gleich 0. | |
| − | + | * Deshalb kommt es hier immer zu einer Überlappung der bedingten Wahrscheinlichkeitsdichtefunktionen <i>f<sub>Y|X</sub></i>(<i>y</i>|–1) und <i>f<sub>Y|X</sub></i>(<i>y</i>|+1.) | |
| − | + | * Entsprechend der Teilaufgabe (4) ist deshalb <i>C</i><sub>BPSK</sub>(<i>E</i><sub>B</sub>/<i>N</i><sub>0</sub>) ≡ 1 bit/Symbol nicht möglich. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 16:21, 14 June 2017
Wir gehen hier von einem binären bipolaren Quellensignal aus ⇒ X = (+1, –1). Die Wahrscheinlichkeitsdichtefunktion (WDF) der Quelle lautet somit:
- $$f_X(x) = {1}/{2} \cdot \delta (x-1) + {1}/{2} \cdot \delta (x+1)\hspace{0.05cm}. $$
Die Transinformation zwischen der Quelle X und der Sinke Y kann gemäß der Gleichung
- $$I(X;Y) = h(Y) - h(N)$$
berechnet werden, wobei gilt:
- $h(Y)$ bezeichnet die differentielle Sinkenentropie
- $$h(Y) = \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{{\rm supp}(f_Y)} \hspace{-0.35cm} f_Y(y) \cdot {\rm log}_2 \hspace{0.1cm} [ f_Y(y) ] \hspace{0.1cm}{\rm d}y \hspace{0.05cm},$$
- $${\rm mit}\hspace{0.5cm} f_Y(y) = {1}/{2} \cdot \left [ f_{Y|{X}}(y|{X}=-1) + f_{Y|{X}}(y|{X}=+1) \right ]\hspace{0.05cm}.$$
- $h(N)$ gibt die differentielle Störentropie an, allein berechenbar aus der WDF $f_N(n)$:
- $$h(N) = \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{{\rm supp}(f_N)} \hspace{-0.35cm} f_N(n) \cdot {\rm log}_2 \hspace{0.1cm} [ f_N(n) ] \hspace{0.1cm}{\rm d}n \hspace{0.05cm}.$$
Nimmt man für die Störung N eine Gaußverteilung fN(n) entsprechend der oberen Skizze an, so ergibt sich die Kanalkapazität CBPSK = I(X; Y), die im Theorieteil abhängig von 10 · lg (EB/N0) dargestellt ist.
Beantwortet werden soll in dieser Aufgabe die Frage, ob es einen endlichen EB/N0–Wert gibt, für den CBPSK(EB/N0) ≡ 1 bit/Kanalzugriff möglich ist ⇒ Teilaufgabe (5).
In den Teilaufgaben (1) bis (4) werden Vorarbeiten zur Beantwortung dieser Frage geleistet. Dabei wird stets von der gleichverteilten Stör–WDF fN(n) ausgegangen (siehe untere Skizze):
- $$f_N(n) = \left\{ \begin{array}{c} 1/(2A) \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.3cm} |n| < A, \\ {\rm{f\ddot{u}r}} \hspace{0.3cm} |n| > A. \\ \end{array} $$
Hinweise:
- Die Aufgabe gehört zum Kapitel AWGN–Kanalkapazität bei wertkontinuierlichem Eingang.
- Bezug genommen wird insbesondere auf die Seite AWGN-Kanalkapazität für binäre Eingangssignale.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
- $$ h(N) = {\rm log}_2 \hspace{0.1cm} (2A) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} A=1/8\hspace{-0.05cm}: \hspace{0.15cm}h(N) = {\rm log}_2 \hspace{0.1cm} (1/4) \hspace{0.15cm}\underline{= -2\,{\rm bit(/Symbol)}}\hspace{0.05cm}.$$
(2) Die Wahrscheinlichkeitsdichtefunktion am Ausgang ergibt sich entsprechend der Gleichung:
- $$f_Y(y) = {1}/{2} \cdot \left [ f_{Y|{X}}(y|-1) + f_{Y|{X}}(y|+1) \right ]\hspace{0.05cm}.$$
Die Grafik zeigt das Ergebnis für unser Beispiel (A = 1/8):
- Rot gezeichnet ist der erste Term 1/2 · fY|X(y|–1), wobei das Rechteck fN(n) an die Stelle Y = –1 verschoben und mit 1/2 multipliziert wird. Es ergibt sich ein Rechteck der Breite 2A = 1/4 und der Höhe 1/(4A) = 2.
- Blau dargestellt ist der zweite Term 1/2 · fY|X(y|+1) mit der Mitte bei Y = +1.
- Lässt man die Farben außer Betracht, so ergibt sich die gesamte WDF fY(y).
Die differentiellen Entropie wird nicht verändert wird, wenn man nicht überlappende WDF–Abschnitte verschiebt. Somit ergibt sich für die gesuchte differentielle Sinkenentropie:
- $$h(Y) = {\rm log}_2 \hspace{0.1cm} (4A) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} A=1/8\hspace{-0.05cm}: \hspace{0.15cm}h(Y) = {\rm log}_2 \hspace{0.1cm} (1/2) \hspace{0.15cm}\underline{= -1\,{\rm bit(/Symbol)}}\hspace{0.05cm}.$$
(3) Damit erhält man für die Transinformation zwischen Quelle und Sinke:
- $$I(X; Y) = h(Y) \hspace{-0.05cm}-\hspace{-0.05cm} h(N) = (-1\,{\rm bit/Symbol})\hspace{-0.05cm} -\hspace{-0.05cm}(-2\,{\rm bit/Symbol}) \hspace{0.15cm}\underline{= +1\,{\rm bit/Symbol}}\hspace{0.05cm}.$$
(4) Alle Lösungsvorschläge sind zutreffend:
- Für jedes A ≤ 1 gilt
- $$ h(Y) = {\rm log}_2 \hspace{0.1cm} (4A) = {\rm log}_2 \hspace{0.1cm} (2A) + {\rm log}_2 \hspace{0.1cm} (2)\hspace{0.05cm}, \hspace{0.5cm} h(N) = {\rm log}_2 \hspace{0.1cm} (2A)$$
- $$\Rightarrow \hspace{0.3cm} I(X; Y) = h(Y) \hspace{-0.05cm}- \hspace{-0.05cm}h(N) = {\rm log}_2 \hspace{0.1cm} (2) \hspace{0.15cm}\underline{= +1\,{\rm bit/Symbol}}\hspace{0.05cm}.$$
- An diesem Prinzip ändert sich auch bei anderer WDF fN(n) nichts, solange die Störung auf den Bereich |n| ≤ 1 begrenzt ist.
- Überlappen sich jedoch die beiden bedingten Wahrscheinlichkeitsdichtefunktionen, so ergibt sich für h(Y) ein kleinerer Wert als oben berechnet und damit auch eine kleinere Transinformation.
(5) Richtig ist der Lösungsvorschlag 2:
- Die Gaußfunktion klingt zwar sehr schnell ab, sie wird aber nie exakt gleich 0.
- Deshalb kommt es hier immer zu einer Überlappung der bedingten Wahrscheinlichkeitsdichtefunktionen fY|X(y|–1) und fY|X(y|+1.)
- Entsprechend der Teilaufgabe (4) ist deshalb CBPSK(EB/N0) ≡ 1 bit/Symbol nicht möglich.