Difference between revisions of "Aufgaben:Exercise 5.4: Comparison of Rectangular and Hanning Window"
| Line 49: | Line 49: | ||
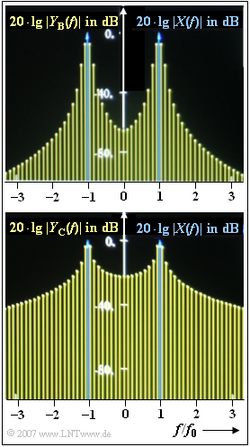
In der obigen Grafik sind zwei weitere Spektralfunktionen $Y_B(f)$ und $Y_C(f)$ abgebildet, die sich ergeben, wenn ein 1 kHz–Signal mittels DFT analysiert wird und der DFT–Parameter $T_P$ = 8.5 ms ungünstig gewählt ist. | In der obigen Grafik sind zwei weitere Spektralfunktionen $Y_B(f)$ und $Y_C(f)$ abgebildet, die sich ergeben, wenn ein 1 kHz–Signal mittels DFT analysiert wird und der DFT–Parameter $T_P$ = 8.5 ms ungünstig gewählt ist. | ||
Für eines der Bilder ist das Rechteckfenster zugrundegelegt, für das andere das Hanning–Fenster. Nicht angegeben wird, welche Spektralfunktion zu welchem Fenster gehört. | Für eines der Bilder ist das Rechteckfenster zugrundegelegt, für das andere das Hanning–Fenster. Nicht angegeben wird, welche Spektralfunktion zu welchem Fenster gehört. | ||
| + | |||
| + | ''Hinweise:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Fehlermöglichkeiten_bei_Anwendung_der_DFT|Fehlermöglichkeiten bei Anwendung der DFT]]. | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| + | *Die Theorie zu diesem Kapitel ist auch im folgenden Lernvideo zusammengefasst: | ||
| + | :[[Fehlermöglichkeiten bei Anwendung der DFT (Dauer 7:26)]] | ||
| + | |||
Hinweis: Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 5.4. | Hinweis: Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 5.4. | ||
Revision as of 15:12, 24 January 2017
Gegeben sei der prinzipielle Zeitverlauf $x(t)$ eines periodischen Signals. Unbekannt sind die Parameter $A_1$, $f_1$, $A_2$ und $f_2$:
$$\begin{align*} x(t) & = A_1 \cdot \cos (2 \pi \cdot f_1 \cdot t) \\ & + A_2 \cdot \cos (2 \pi \cdot f_2 \cdot t) \hspace{0.05cm}.\end{align*}$$
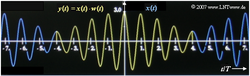
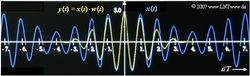
Nach Gewichtung des Signals mit dem Fenster $w(t)$ wird das Produkt $y(t) = x(t) \cdot w(t)$ einer Diskreten Fouriertransformation (DFT) mit den Parametern $N$ = 512 und $T_P$ unterworfen. Die Zeitdauer $T_P$ des analysierten Signalausschnitts kann vom Benutzer beliebig eingestellt werden. Für die Fensterung stehen folgende Funktionen zur Verfügung, die jeweils für $|t| > T_P/2$ identisch 0 sind: das Rechteckfenster:
$${w} (\nu) = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ \\ \end{array}\begin{array}{*{20}c} -N/2 \le \nu < N/2 \hspace{0.05cm}, \\ {\rm sonst} \hspace{0.05cm}, \\ \end{array}$$
$$W(f) ={1}/{f_{\rm A}}\cdot {\rm si}(\pi \cdot {f}/{f_{\rm A}})\hspace{0.05cm},$$
das Hanning–Fenster:
$${w} (\nu) = \left\{ \begin{array}{c} 0.5 + 0.5 \cdot \cos (2 \pi \cdot \frac{\nu}{N}) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ \\ \end{array}\begin{array}{*{20}c} -N/2 \le \nu < N/2 \hspace{0.05cm}, \\ {\rm sonst} \hspace{0.05cm}, \\ \end{array}$$
$$W(f) ={0.5}/{f_{\rm A}}\cdot {\rm si}(\pi \cdot \frac{f}{f_{\rm A}})+ {0.25}/{f_{\rm A}}\cdot {\rm si}(\pi \cdot \frac{f-f_{\rm A}}{f_{\rm A}})+ {0.5}/{f_{\rm A}}\cdot {\rm si}(\pi \cdot \frac{f+f_{\rm A}}{f_{\rm A}})\hspace{0.05cm}.$$
Beachten Sie, dass die Frequenzauflösung $f_A$ gleich dem Kehrwert des einstellbaren Parameters $T_P$ ist. $W(f)$ ist die Fouriertransformierte der zeitkontinuierlichen Fensterfunktion $w(t)$, während die oben angegebene Funktion $w(ν)$ die zeitdiskrete Gewichtungsfunktion angibt. Im Laufe der Aufgabe wird auf verschiedene Spektralfunktionen $Y(f)$ Bezug genommen, zum Beispiel auf
$$Y_{\rm A}(f) = 1\, {\rm V}\cdot {\rm \delta} (f \pm 1\,\,{\rm kHz})+ 0.5\,\, {\rm V}\cdot {\rm \delta} (f \pm 1.125\,\,{\rm kHz}) \hspace{0.05cm}.$$
In der obigen Grafik sind zwei weitere Spektralfunktionen $Y_B(f)$ und $Y_C(f)$ abgebildet, die sich ergeben, wenn ein 1 kHz–Signal mittels DFT analysiert wird und der DFT–Parameter $T_P$ = 8.5 ms ungünstig gewählt ist. Für eines der Bilder ist das Rechteckfenster zugrundegelegt, für das andere das Hanning–Fenster. Nicht angegeben wird, welche Spektralfunktion zu welchem Fenster gehört.
Hinweise:
- Die Aufgabe gehört zum Kapitel Fehlermöglichkeiten bei Anwendung der DFT.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Die Theorie zu diesem Kapitel ist auch im folgenden Lernvideo zusammengefasst:
Hinweis: Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 5.4.
Fragebogen
Musterlösung
2. Wegen $T_P$ = 8 ms setzt sich das Hanning–Spektrum $W(f)$ aus drei Diracfunktionen bei positiven Frequenzen und drei dazu achsensymmetrischen Diracs bei negativen Frequenzen zusammen. Für die positiven Frequenzen lautet die Spektralfunktion:
$$W(f) =0.5\cdot {\rm \delta}(f) + 0.25\cdot {\rm \delta}(f-f_{\rm A})+ 0.25\cdot {\rm \delta}(f+f_{\rm A})\hspace{0.05cm}.$$
Das Ausgangsspektrum ergibt sich aus der Faltung zwischen $X(f)$ und $W(f)$. Bei positiven Frequenzen ergeben sich nun vier Diracs mit folgenden Gewichten:
$$\begin{align*} G(f = 0.875\,{\rm kHz}) & = 1\, {\rm V}\cdot 0.25 = 0.250\, {\rm V}, \\ G(f = f_1 = 1.000\,{\rm kHz}) & = 1\, {\rm V}\cdot 0.5 + 0.5\, {\rm V}\cdot 0.25 \hspace{0.15 cm}\underline{ = 0.625\, {\rm V}}, \\ G(f = f_2 = 1.125\,{\rm kHz}) & = 1\, {\rm V}\cdot 0.25 + 0.5\, {\rm V}\cdot 0.5 \hspace{0.15 cm}\underline{= 0.500\, {\rm V}}, \\ G(f = 1.250\,{\rm kHz}) & = 0.5\, {\rm V}\cdot 0.25 = 0.125\, {\rm V} \hspace{0.05cm}.\end{align*}$$
Die folgende Grafik zeigt die Abschwächung der Ränder durch die Gewichtungsfunktion $w(t)$ des Hanning–Fensters.
3. Das Rechteck–Fenster liefert dann ein sehr stark verfälschtes Ergebnis, wenn die Fensterbreite $T_P$ (wie hier) nicht an die Frequenz des Cosinussignals angepasst ist. In diesem Fall ist das Hanning–Fenster besser geeignet. Daraus folgt: Richtig ist der zweite Lösungsvorschlag.