AWGN Channel Capacity for Continuous-Valued Input

Mutual information between continuous-value random variables

In the chapter Information-theoretical model of digital signal transmission the mutual information between the two discrete-value random variables $X$ and $Y$ was given, among other things, in the following form:

$$I(X;Y) = \hspace{-0.4cm} \sum_{(x,\hspace{0.05cm} y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{XY}\hspace{-0.08cm})} \hspace{-0.8cm} P_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{ P_{XY}(x, y)}{P_{X}(x) \cdot P_{Y}(y)} \hspace{0.05cm}.$$

This equation simultaneously corresponds to the Kullback–Leibler distance between the joint probability function $P_{XY}$ and the product of the two individual probability functions $P_X$ and $P_Y$ :

$$I(X;Y) = D(P_{XY} \hspace{0.05cm} || \hspace{0.05cm}P_{X} \cdot P_{Y}) \hspace{0.05cm}.$$

In order to derive the mutual information $I(X; Y)$ between two continuous-value random variables $X$ and $Y$ , one proceeds as follows, whereby inverted commas indicate a quantised variable:

One quantises the random variables $X$ and $Y$ $($with the quantisation intervals ${\it Δ}x$ and ${\it Δ}y)$ and thus obtains the probability functions $P_{X\hspace{0.01cm}′}$ and $P_{Y\hspace{0.01cm}′}$.
The „vectors” $P_{X\hspace{0.01cm}′}$ and $P_{Y\hspace{0.01cm}′}$ become infinitely long after the boundary transitions ${\it Δ}x → 0, {\it Δ}y → 0$ , and the joint PMF $P_{X\hspace{0.01cm}′\hspace{0.08cm}Y\hspace{0.01cm}′}$ is then also infinitely extended in area.
These boundary transitions give rise to the probability density functions of the continuous random variables according to the following equations:

$$f_X(x_{\mu}) = \frac{P_{X\hspace{0.01cm}'}(x_{\mu})}{\it \Delta_x} \hspace{0.05cm}, \hspace{0.3cm}f_Y(y_{\mu}) = \frac{P_{Y\hspace{0.01cm}'}(y_{\mu})}{\it \Delta_y} \hspace{0.05cm}, \hspace{0.3cm}f_{XY}(x_{\mu}\hspace{0.05cm}, y_{\mu}) = \frac{P_{X\hspace{0.01cm}'\hspace{0.03cm}Y\hspace{0.01cm}'}(x_{\mu}\hspace{0.05cm}, y_{\mu})} {{\it \Delta_x} \cdot {\it \Delta_y}} \hspace{0.05cm}.$$

The double sum in the above equation, after renaming $Δx → {\rm d}x$ or $Δy → {\rm d}y$ , becomes the equation valid for continuous value random variables:

$$I(X;Y) = \hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.4cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm} (\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{ f_{XY}(x, y) } {f_{X}(x) \cdot f_{Y}(y)} \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y \hspace{0.05cm}.$$

$\text{Conclusion:}$ By splitting this double integral, it is also possible to write for the transinformation:

$$I(X;Y) = h(X) + h(Y) - h(XY)\hspace{0.05cm}.$$

The joint differential entropy

$$h(XY) = -\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.4cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm} (\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \big[f_{XY}(x, y) \big] \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y$$

and the two differential single entropies

$$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}\hspace{0.03cm} (\hspace{-0.03cm}f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big[f_X(x)\big] \hspace{0.1cm}{\rm d}x \hspace{0.05cm},\hspace{0.5cm} h(Y) = -\hspace{-0.7cm} \int\limits_{y \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}\hspace{0.03cm} (\hspace{-0.03cm}f_Y)} \hspace{-0.35cm} f_Y(y) \cdot {\rm log} \hspace{0.1cm} \big[f_Y(y)\big] \hspace{0.1cm}{\rm d}y \hspace{0.05cm}.$$

On equivocation and irrelevance

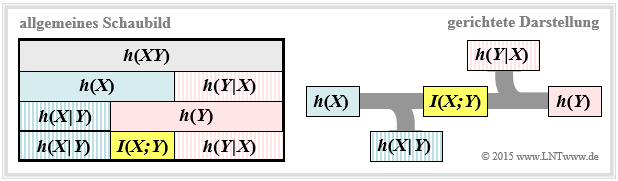
We further assume the continuous value mutual information $I(X;Y) = h(X) + h(Y) - h(XY)$ . This representation is also found in the following diagram (left graph).

Representation of the mutual information for continuous value random variables

From this you can see that the mutual information can also be represented as follows:

$$I(X;Y) = h(Y) - h(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) =h(X) - h(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y)\hspace{0.05cm}.$$

These fundamental information-theoretical relationships can also be read from the graph on the right.

This directional representation is particularly suitable for message transmission systems.

The outflowing or inflowing differential entropy characterises

the equivocation:

$$h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) =\hspace{0.2cm} -\int \hspace{-0.9cm} \int\limits_{\hspace{-0.4cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.03cm} (\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \big [{f_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (x \hspace{-0.05cm}\mid \hspace{-0.05cm} y)} \big] \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm},$$

the irrelevance:

$$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) =\hspace{0.2cm}- \int \hspace{-0.9cm} \int\limits_{\hspace{-0.4cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.03cm} (\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \big [{f_{\hspace{0.03cm}Y \mid \hspace{0.03cm} X} (y \hspace{-0.05cm}\mid \hspace{-0.05cm} x)} \big] \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm}.$$

The significance of these two information-theoretic quantities will be discussed in more detail in task 4.5Z .

If one compares the graphical representations of the mutual information for

discrete value random variables in the section [[Information_Theory/Anwendung_auf_die_Digitalsignalübertragung#Information-theoretical_model_of_digital_signal_transmission|Information-theoretical model of digital signal transmission] continuous value random variables according to the above diagram,

the only distinguishing feature is that each „capital $H$” (entropy; larger-equal zero) has been replaced by a „non-capital $h$” (differential entropy can be positive, negative or zero) .

Otherwise, the mutual information is the same in both representations and $I(X; Y) ≥ 0$ always applies.
In the following, we mostly use the binary logarithm ⇒ $\log_2$ and thus obtain the mutual information in „bit”.

Calculation of mutual information with additive noise

We now consider a very simple model of message transmission:

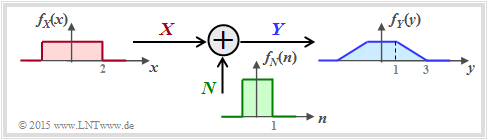
The random variable $X$ stands for the (zero mean) transmission signal and is characterised by the PDF $f_X(x)$ and the variance $σ_X^2$ . The transmission power is $P_X = σ_X^2$.
The additive noise $N$ is given by the PDF $f_N(n)$ and the noise power $P_N = σ_N^2$ .
If $X$ and $N$ are assumed to be statistically independent ⇒ signal-independent noise, then $\text{E}\big[X · N \big] = \text{E}\big[X \big] · \text{E}\big[N\big] = 0$ .
The received signal is $Y = X + N$. The output PDF $f_Y(y)$ can be calculated with the convolution operation ⇒ $f_Y(y) = f_X(x) ∗ f_N(n)$.

Message transmission system with additive noise

For the received power (variance) holds:

$$P_Y = \sigma_Y^2 = {\rm E}\big[Y^2\big] = {\rm E}\big[(X+N)^2\big] = {\rm E}\big[X^2\big] + {\rm E}\big[N^2\big] = \sigma_X^2 + \sigma_N^2 $$

$$\Rightarrow \hspace{0.3cm} P_Y = P_X + P_N \hspace{0.05cm}.$$

The sketched density functions sketched (rectangular or trapezoidal) are only intended to clarify the calculation process and have no practical relevance.
To calculate the mutual information between input $X$ and output $Y$ there are three possibilities according to the graphic on the previous subchapter drei Möglichkeiten:

Calculation according to $I(X, Y) = h(X) + h(Y) - h(XY)$:

The first two terms can be calculated in a simple way from $f_X(x)$ and $f_Y(y)$ respectively. The joint differentrial entropy $h(XY)$ is problematic. For this, one needs the 2D joint PDF $f_{XY}(x, y)$, which is usually not given directly.

Calculation according to $I(X, Y) = h(Y) - h(Y|X)$:

Here $h(Y|X)$ denotes the differential scattering entropy. It holds that $h(Y|X) = h(X + N|X) = h(N)$, so that $I(X; Y)$ is very easy to calculate via the equation $f_Y(y) = f_X(x) ∗ f_N(n)$ if $f_X(x)$ and $f_N(n)$ are known.

Calculation according to $I(X, Y) = h(X) - h(X|Y)$:

According to this equation, however, one needs the differential inference entropy $h(X|Y)$, which is more difficult to state than $h(Y|X)$.

$\text{Conclusion:}$ In the following we use the middle equation and write for the mutual information between the input $X$ and the output $Y$ of a message transmission system in the presence of additive and uncorrelated noise $N$:

$$I(X;Y) \hspace{-0.05cm} = \hspace{-0.01cm} h(Y) \hspace{-0.01cm}- \hspace{-0.01cm}h(N) \hspace{-0.01cm}=\hspace{-0.05cm} -\hspace{-0.7cm} \int\limits_{y \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_Y)} \hspace{-0.65cm} f_Y(y) \cdot {\rm log} \hspace{0.1cm} \big[f_Y(y)\big] \hspace{0.1cm}{\rm d}y +\hspace{-0.7cm} \int\limits_{n \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_N)} \hspace{-0.65cm} f_N(n) \cdot {\rm log} \hspace{0.1cm} \big[f_N(n)\big] \hspace{0.1cm}{\rm d}n\hspace{0.05cm}.$$

Channel capacity of the AWGN channel

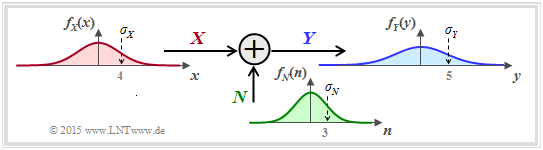
If one specifies the probability density function of the noise in the previous general system model as Gaussian corresponding to

Derivation of the AWGN channel capacity

$$f_N(n) = \frac{1}{\sqrt{2\pi \sigma_N^2}} \cdot {\rm e}^{ - \hspace{0.05cm}{n^2}/(2 \sigma_N^2) } \hspace{0.05cm}, $$

we obtain the model sketched on the right for calculating the channel capacity of the so-called AWGN channel (Additive White Gaussian Noise). In the following, we usually replace $\sigma_N^2$ by $P_N$.
We know from previous sections:

The channel capacity $C_{\rm AWGN}$ specifies the maximum mutual information $I(X; Y)$ between the input quantity $X$ and the output quantity $Y$ of the AWGN channel. The maximisation refers to the best possible input PDF. Thus, under the power constraint the following applies:

$$C_{\rm AWGN} = \max_{f_X:\hspace{0.1cm} {\rm E}[X^2 ] \le P_X} \hspace{-0.35cm} I(X;Y) = -h(N) + \max_{f_X:\hspace{0.1cm} {\rm E}[X^2] \le P_X} \hspace{-0.35cm} h(Y) \hspace{0.05cm}.$$

It is already taken into account that the maximisation relates solely to the differential entropy $h(Y)$ ⇒ PDF $f_Y(y)$ bezieht. Indeed, for a given noise power $P_N$ , $h(N) = 1/2 · \log_2 (2π{\rm e} · P_N)$ is a constant.

The maximum for $h(Y)$ is obtained for a Gaussian PDF $f_Y(y)$ with $P_Y = P_X + P_N$ t, see page maximum differential entropy under power constraint:

$${\rm max}\big[h(Y)\big] = 1/2 · \log_2 \big[2πe · (P_X + P_N)\big].$$

However, the output PDF $f_Y(y) = f_X(x) ∗ f_N(n)$ is Gaussian only if both $f_X(x)$ and $f_N(n)$ are Gaussian functions. A striking saying about the convolution operation is: Gaussian remains Gaussian, and non-Gaussian never becomes (exactly) Gaussian.

$\text{Conclusion:}$ For the AWGN channel ⇒ Gaussian noise PDF $f_N(n)$ the channel capacity results exactly when the input PDF $f_X(x)$ is also Gaussian:

Numerical results for the AWGN channel capacity as a function of ${P_X}/{P_N}$

$$C_{\rm AWGN} = h_{\rm max}(Y) - h(N) = 1/2 \cdot {\rm log}_2 \hspace{0.1cm} {P_Y}/{P_N}$$

$$\Rightarrow \hspace{0.3cm} C_{\rm AWGN}= 1/2 \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + P_X/P_N) \hspace{0.05cm}.$$

Parallel Gaussian channels

Parallel AWGN channels

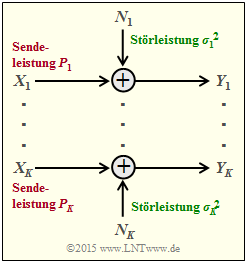
We now consider, according to the graph $K$ parallel Gaussian channels of $X_1 → Y_1$, ... , $X_k → Y_k$, ... , $X_K → Y_K$.

We call the transmission powers in the $K$ channels

$$P_1 = \text{E}[X_1^2], \hspace{0.15cm}\text{...}\hspace{0.15cm} ,\ P_k = \text{E}[X_k^2], \hspace{0.15cm}\text{...}\hspace{0.15cm} ,\ P_K = \text{E}[X_K^2].$$

The $K$ noise powers can also be different:

$$σ_1^2, \hspace{0.15cm}\text{...}\hspace{0.15cm} ,\ σ_k^2, \hspace{0.15cm}\text{...}\hspace{0.15cm} ,\ σ_K^2.$$

We are now looking for the maximum mutual information $I(X_1, \hspace{0.15cm}\text{...}\hspace{0.15cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, \hspace{0.15cm}\text{...}\hspace{0.15cm}, Y_K) $ between

the $K$ input variables $X_1$, ... , $X_K$ and
the $K$ output variables $Y_1$ , ... , $Y_K$,

which we call the total channel capacity of this AWGN configuration.

$\text{Agreement:}$ AAssume power constraint of the total system. That is:
The sum of all powers $P_k$ in the $K$ individual channels must not exceed the specified value $P_X$ :

$$P_1 + \hspace{0.05cm}\text{...}\hspace{0.05cm}+ P_K = \hspace{0.1cm} \sum_{k= 1}^K \hspace{0.1cm}{\rm E} \left [ X_k^2\right ] \le P_{X} \hspace{0.05cm}.$$

Under the only slightly restrictive assumption of independent noise sources $N_1$, ... , $N_K$ can be written for the mutual information after some intermediate steps:

$$I(X_1, \hspace{0.05cm}\text{...}\hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1,\hspace{0.05cm}\text{...}\hspace{0.05cm}, Y_K) = h(Y_1, ... \hspace{0.05cm}, Y_K ) - \hspace{0.1cm} \sum_{k= 1}^K \hspace{0.1cm} h(N_k)\hspace{0.05cm}.$$

The following upper bound can be specified for this:

$$I(X_1,\hspace{0.05cm}\text{...}\hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, Y_K) \hspace{0.2cm} \le \hspace{0.1cm} \hspace{0.1cm} \sum_{k= 1}^K \hspace{0.1cm} \big[h(Y_k - h(N_k)\big] \hspace{0.2cm} \le \hspace{0.1cm} 1/2 \cdot \sum_{k= 1}^K \hspace{0.1cm} {\rm log}_2 \hspace{0.1cm} ( 1 + {P_k}/{\sigma_k^2}) \hspace{0.05cm}.$$

The equal sign (identity) is valid for mean-free Gaussian input variables $X_k$ as well as for statistically independent disturbances $N_k$.
One arrives from this equation at the maximum mutual information ⇒ channel capacity, if the total transmission power $P_X$ is divided as best as possible, taking into account the different interferences in the individual channels $(σ_k^2)$ .
This optimisation problem can again be elegantly solved with the method of Lagrange multipliers elegant lösen. The following example only explains the result.

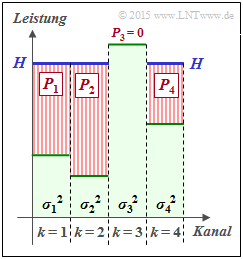
Best possible power division for $K = 4$ („Water–Filling”)

$\text{Beispiel 1:}$ We consider $K = 4$ parallel Gaussian channels with four different noise powers $σ_1^2$, ... , $σ_4^2$ according to the adjacent figure (faint green background).

The best possible distribution of the transmitting power among the four channels is sought.
If one were to slowly fill this profile with water, the water would initially flow only into $\text{channel 2}$ .
If you continue to pour, some water will also accumulate in $\text{channel 1}$ and later also in $\text{channel 4}$.

The drawn „water level” $H$ describes exactly the point in time when the sum $P_1 + P_2 + P_4$ corresponds to the total available transmitting power $P_X$ :

The optimal power distribution for this example results in $P_2 > P_1 > P_4$ as well as $P_3 = 0$.
Only with a larger transmitting power $P_X$ would a small power $P_3$ also be allocated to the third channel.

This allocation procedure is called a Water–Filling algorithm.

$\text{Example 2:}$ If all $K$ Gaussian channels are equally disturbed ⇒ $σ_1^2 = \hspace{0.15cm}\text{...}\hspace{0.15cm} = σ_K^2 = P_N$,one should naturally distribute the total available transmit power $P_X$ equally to all channels:: $P_k = P_X/K$. For the total capacity one then obtains:

Capacity for $K$ parallel channels

$$C_{\rm Gesamt} = \frac{ K}{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac{P_X}{K \cdot P_N}) \hspace{0.05cm}.$$

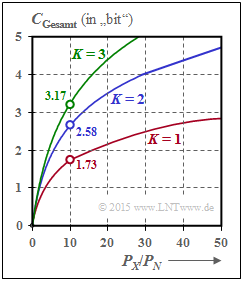
The graph shows the total capacity as a function of $P_X/P_N$ for $K = 1$, $K = 2$ and $K = 3$:

For $P_X/P_N = 10 \ ⇒ \ 10 · \text{lg} (P_X/P_N) = 10 \ \text{dB}$ , the total capacitance becomes approximately $50\%$ larger if the total power $P_X$ is divided equally between two channels: $P_1 = P_2 = P_X/2$.
In the borderline case $P_X/P_N → ∞$ , the total capacity increases by a factor $K$ ⇒ doubling at $K = 2$.

The two identical and independent channels can be realised in different ways, for example by multiplexing in time, frequency or space.

However, the case $K = 2$ can also be realised by using orthogonal basis functions such as „cosine” und „sine” as for example with