Difference between revisions of "Information Theory/Discrete Memoryless Sources"
| Line 37: | Line 37: | ||
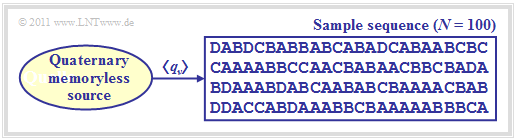
The figure shows a quaternary message source $(M = 4)$ with the alphabet $\rm \{A, \ B, \ C, \ D\}$ and an exemplary sequence of length $N = 100$. | The figure shows a quaternary message source $(M = 4)$ with the alphabet $\rm \{A, \ B, \ C, \ D\}$ and an exemplary sequence of length $N = 100$. | ||
| − | [[File: | + | [[File:EN_Inf_T_1_1_S1a.png|frame|Memoryless Quaternary Message Source]] |
The following requirements apply: | The following requirements apply: | ||
| Line 183: | Line 183: | ||
The figure shows the binary entropy function for the values $0 ≤ p ≤ 1$ of the symbol probability of $\rm A$ $($or also of $\rm B)$. You can see | The figure shows the binary entropy function for the values $0 ≤ p ≤ 1$ of the symbol probability of $\rm A$ $($or also of $\rm B)$. You can see | ||
| − | [[File: | + | [[File:EN_Inf_T_1_1_S4.png|frame|Binary entropy function as function of $p$|right]] |
*The maximum value $H_\text{max} = 1\; \rm bit$ results for $p = 0.5$, thus for equally probable binary symbols. Then $\rm A$ and $\rm B$ contribute the same amount to entropy. | *The maximum value $H_\text{max} = 1\; \rm bit$ results for $p = 0.5$, thus for equally probable binary symbols. Then $\rm A$ and $\rm B$ contribute the same amount to entropy. | ||
* $H_\text{bin}(p)$ is symmetrical about $p = 0.5$. A source with $p_{\rm A} = 0.1$ and $p_{\rm B} = 0. 9$ has the same entropy $H = 0.469 \; \rm bit$ as a source with $p_{\rm A} = 0.9$ and $p_{\rm B} = 0.1$. | * $H_\text{bin}(p)$ is symmetrical about $p = 0.5$. A source with $p_{\rm A} = 0.1$ and $p_{\rm B} = 0. 9$ has the same entropy $H = 0.469 \; \rm bit$ as a source with $p_{\rm A} = 0.9$ and $p_{\rm B} = 0.1$. | ||
| Line 206: | Line 206: | ||
$\text{Example 3:}$ | $\text{Example 3:}$ | ||
Now there are certain symmetries between the symbol probabilities: | Now there are certain symmetries between the symbol probabilities: | ||
| − | [[File: | + | [[File:EN_Inf_T_1_1_S5.png|frame|Entropy of binary source and quaternary source]] |
:$$p_{\rm A} = p_{\rm D} = p \hspace{0.05cm},\hspace{0.4cm}p_{\rm B} = p_{\rm C} = 0.5 - p \hspace{0.05cm},\hspace{0.3cm}{\rm with} \hspace{0.15cm}0 \le p \le 0.5 \hspace{0.05cm}.$$ | :$$p_{\rm A} = p_{\rm D} = p \hspace{0.05cm},\hspace{0.4cm}p_{\rm B} = p_{\rm C} = 0.5 - p \hspace{0.05cm},\hspace{0.3cm}{\rm with} \hspace{0.15cm}0 \le p \le 0.5 \hspace{0.05cm}.$$ | ||
Revision as of 15:03, 15 June 2021
Contents
# OVERVIEW OF THE FIRST MAIN CHAPTER #
This first chapter describes the calculation and the meaning of entropy. According to the Shannonian information definition, entropy is a measure of the mean uncertainty about the outcome of a statistical event or the uncertainty in the measurement of a stochastic quantity. Somewhat casually expressed, the entropy of a random quantity quantifies its "randomness".
In detail are discussed:
- the decision content and the entropy of a memoryless news source,
- the binary entropy function and its application to non-binary sources,
- the entropy calculation for memory sources and suitable approximations,
- the peculiarities of Markov sources regarding the entropy calculation,
- the procedure for sources with a large number of symbols, for example natural texts,
- the entropy estimates according to Shannon and Küpfmüller.
Further information on the topic as well as Exercises, simulations and programming exercises can be found in the experiment "Value Discrete Information Theory" of the practical course "Simulation Digitaler Übertragungssysteme" (english: Simulation of Digital Transmission Systems). This (former) LNT course at the TU Munich is based on
- the Windows program WDIT ⇒ the link points to the ZIP version of the program and
- the associated Internship guide ⇒ the link refers to the PDF version.
Model and requirements
We consider a value discrete message source $\rm Q$, which gives a sequence $ \langle q_ν \rangle$ of symbols.
- For the run variable $ν = 1$, ... , $N$, where $N$ should be "sufficiently large".
- Each individual source symbol $q_ν$ comes from a symbol set $\{q_μ \}$ where $μ = 1$, ... , $M$, where $M$ denotes the symbol range:
- $$q_{\nu} \in \left \{ q_{\mu} \right \}, \hspace{0.25cm}{\rm with}\hspace{0.25cm} \nu = 1, \hspace{0.05cm} \text{ ...}\hspace{0.05cm} , N\hspace{0.25cm}{\rm and}\hspace{0.25cm}\mu = 1,\hspace{0.05cm} \text{ ...}\hspace{0.05cm} , M \hspace{0.05cm}.$$
The figure shows a quaternary message source $(M = 4)$ with the alphabet $\rm \{A, \ B, \ C, \ D\}$ and an exemplary sequence of length $N = 100$.
The following requirements apply:
- The quaternary news source is fully described by $M = 4$ symbol probabilities $p_μ$. In general it applies:
- $$\sum_{\mu = 1}^M \hspace{0.1cm}p_{\mu} = 1 \hspace{0.05cm}.$$
- The message source is memoryless, i.e., the individual sequence elements are statistically independent of each other:
- $${\rm Pr} \left (q_{\nu} = q_{\mu} \right ) = {\rm Pr} \left (q_{\nu} = q_{\mu} \hspace{0.03cm} | \hspace{0.03cm} q_{\nu -1}, q_{\nu -2}, \hspace{0.05cm} \text{ ...}\hspace{0.05cm}\right ) \hspace{0.05cm}.$$
- Since the alphabet consists of symbols (and not of random variables) , the specification of expected values (linear mean, quadratic mean, dispersion, etc.) is not possible here, but also not necessary from an information-theoretical point of view.
These properties will now be illustrated with an example.
$\text{Example 1:}$ For the symbol probabilities of a quaternary source applies:
- $$p_{\rm A} = 0.4 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.3 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.2 \hspace{0.05cm},\hspace{0.2cm} p_{\rm D} = 0.1\hspace{0.05cm}.$$
For an infinitely long sequence $(N \to \infty)$
- the relative frequencies $h_{\rm A}$, $h_{\rm B}$, $h_{\rm C}$, $h_{\rm D}$ ⇒ a-posteriori parameters
- were identical to the probabilities $p_{\rm A}$, $p_{\rm B}$, $p_{\rm C}$, $p_{\rm D}$ ⇒ a-priori parameters.
With smaller $N$ deviations may occur, as the adjacent table (result of a simulation) shows.
- In the graphic above an exemplary sequence is shown with $N = 100$ symbols.
- Due to the set elements $\rm A$, $\rm B$, $\rm C$ and $\rm D$ no mean values can be given.
However, if you replace the symbols with numerical values, for example $\rm A \Rightarrow 1$, $\rm B \Rightarrow 2$, $\rm C \Rightarrow 3$, $\rm D \Rightarrow 4$, then you will get
time averaging ⇒ crossing line or ensemble averaging ⇒ expected value formation
- for the linear average :
- $$m_1 = \overline { q_{\nu} } = {\rm E} \big [ q_{\mu} \big ] = 0.4 \cdot 1 + 0.3 \cdot 2 + 0.2 \cdot 3 + 0.1 \cdot 4 = 2 \hspace{0.05cm},$$
- for the square mean:
- $$m_2 = \overline { q_{\nu}^{\hspace{0.05cm}2} } = {\rm E} \big [ q_{\mu}^{\hspace{0.05cm}2} \big ] = 0.4 \cdot 1^2 + 0.3 \cdot 2^2 + 0.2 \cdot 3^2 + 0.1 \cdot 4^2 = 5 \hspace{0.05cm},$$
- for the standard deviation (scattering) according to the "Theorem of Steiner":
- $$\sigma = \sqrt {m_2 - m_1^2} = \sqrt {5 - 2^2} = 1 \hspace{0.05cm}.$$
Decision content - Message content
Claude Elwood Shannon defined in 1948 in the standard work of information theory [Sha48][1] the concept of information as "decrease of uncertainty about the occurrence of a statistical event".
Let us make a mental experiment with $M$ possible results, which are all equally probable: $p_1 = p_2 = \hspace{0.05cm} \text{ ...}\hspace{0.05cm} = p_M = 1/M \hspace{0.05cm}.$
Under this assumption applies:
- Is $M = 1$, then each individual attempt will yield the same result and therefore there is no uncertainty about the output.
- On the other hand, an observer learns about an experiment with $M = 2$, for example the "coin toss" with the set of events $\big \{\rm \boldsymbol{\rm Z}, \rm \boldsymbol{\rm W} \big \}$ and the probabilities $p_{\rm Z} = p_{\rm W} = 0. 5$, a gain in information; The uncertainty regarding $\rm Z$ resp. $\rm W$ is resolved.
- In the experiment "dice" $(M = 6)$ and even more in roulette $(M = 37)$ the gained information is even more significant for the observer than in the "coin toss" when he learns which number was thrown or which ball fell.
- Finally it should be considered that the experiment "triple coin toss" with the $M = 8$ possible results $\rm ZZZ$, $\rm ZZW$, $\rm ZWZ$, $\rm ZWW$, $\rm WZZ$, $\rm WZW$, $\rm WWZ$, $\rm WWW$ provides three times the information as the single coin toss $(M = 2)$.
The following definition fulfills all the requirements listed here for a quantitative information measure for equally probable events, indicated only by the symbol range $M$.
$\text{Definition:}$ The decision content of a message source depends only on the symbol range $M$ and results in
- $$H_0 = {\rm log}\hspace{0.1cm}M = {\rm log}_2\hspace{0.1cm}M \hspace{0.15cm} {\rm (in \ “bit")} = {\rm ln}\hspace{0.1cm}M \hspace{0.15cm}\text {(in “nat")} = {\rm lg}\hspace{0.1cm}M \hspace{0.15cm}\text {(in “Hartley")}\hspace{0.05cm}.$$
- The term message content is also commonly used for this.
- Since $H_0$ indicates the maximum value of the Entropy $H$ , $H_\text{max}$ is also used in our tutorial as short notation .
Please note our nomenclature:
- The logarithm will be called "log" in the following, independent of the base.
- The relations mentioned above are fulfilled due to the following properties:
- $${\rm log}\hspace{0.1cm}1 = 0 \hspace{0.05cm},\hspace{0.2cm} {\rm log}\hspace{0.1cm}37 > {\rm log}\hspace{0.1cm}6 > {\rm log}\hspace{0.1cm}2\hspace{0.05cm},\hspace{0.2cm} {\rm log}\hspace{0.1cm}M^k = k \cdot {\rm log}\hspace{0.1cm}M \hspace{0.05cm}.$$
- Usually we use the logarithm to the base $2$ ⇒ Logarithm dualis $\rm (ld)$, where the pseudo unit "bit", more precisely: "bit/symbol", is then added:
- $${\rm ld}\hspace{0.1cm}M = {\rm log_2}\hspace{0.1cm}M = \frac{{\rm lg}\hspace{0.1cm}M}{{\rm lg}\hspace{0.1cm}2} = \frac{{\rm ln}\hspace{0.1cm}M}{{\rm ln}\hspace{0.1cm}2} \hspace{0.05cm}.$$
- In addition, you can find in the literature some additional definitions, which are based on the natural logarithm $\rm (ln)$ or the logarithm $\rm (lg)$ .
Information content and entropy
We now waive the previous requirement that all $M$ possible results of an experiment are equally probable. In order to keep the spelling as compact as possible, we define for this page only:
- $$p_1 > p_2 > \hspace{0.05cm} \text{ ...}\hspace{0.05cm} > p_\mu > \hspace{0.05cm} \text{ ...}\hspace{0.05cm} > p_{M-1} > p_M\hspace{0.05cm},\hspace{0.4cm}\sum_{\mu = 1}^M p_{\mu} = 1 \hspace{0.05cm}.$$
We now consider the information content of the individual symbols, where we denote the "logarithm dualis" with $\log_2$:
- $$I_\mu = {\rm log_2}\hspace{0.1cm}\frac{1}{p_\mu}= -\hspace{0.05cm}{\rm log_2}\hspace{0.1cm}{p_\mu} \hspace{0.5cm}{\rm (unit\hspace{-0.15cm}: \hspace{0.15cm}bit\hspace{0.15cm}or\hspace{0.15cm}bit/Symbol)} \hspace{0.05cm}.$$
You can see:
- because of $p_μ ≤ 1$ the information content is never negative. In the borderline case $p_μ \to 1$ goes $I_μ \to 0$.
- However for $I_μ = 0$ ⇒ $p_μ = 1$ ⇒ $M = 1$ the decision content is also $H_0 = 0$.
- For decreasing probabilities $p_μ$ the information content increases continuously:
- $$I_1 < I_2 < \hspace{0.05cm} \text{ ...}\hspace{0.05cm} < I_\mu <\hspace{0.05cm} \text{ ...}\hspace{0.05cm} < I_{M-1} < I_M \hspace{0.05cm}.$$
$\text{Conclusion:}$ The more improbable an event is, the greater is its information content. This fact is also found in daily life:
- "6 right ones" in the lottery are more likely to be noticed than "3 right ones" or no win at all.
- A tsunami in Asia also dominates the news in Germany for weeks as opposed to the almost standard Deutsche Bahn delays.
- A series of defeats of Bayern Munich leads to huge headlines in contrast to a winning series. With 1860 Munich exactly the opposite is the case.
However, the information content of a single symbol (or event) is not very interesting. On the other hand
- by ensemble averaging over all possible symbols $q_μ$ bzw.
- by time averaging over all elements of the sequence $\langle q_ν \rangle$
one of the central variables of information theory.
$\text{Definition:}$ The Entropy $H$ of a source indicates the mean information content of all symbols :
- $$H = \overline{I_\nu} = {\rm E}\hspace{0.01cm}[I_\mu] = \sum_{\mu = 1}^M p_{\mu} \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{p_\mu}= -\sum_{\mu = 1}^M p_{\mu} \cdot{\rm log_2}\hspace{0.1cm}{p_\mu} \hspace{0.5cm}\text{(unit: bit, more precisely: bit/symbol)} \hspace{0.05cm}.$$
The overline marks again a time averaging and $\rm E[\text{...}]$ a ensemble averaging.
Entropy is among other things a measure for
- the mean uncertainty about the outcome of a statistical event,
- the "randomness" of this event, and
- the average information content of a random variable.
Binary entropy function
At first we will restrict ourselves to the special case $M = 2$ and consider a binary source, which returns the two symbols $\rm A$ and $\rm B$ The occurrence probabilities are $p_{\rm A} = p$ and $p_{\rm B} = 1 - p$.
For the entropy of this binary source applies:
- $$H_{\rm bin} (p) = p \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p\hspace{0.1cm}} + (1-p) \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{1-p} \hspace{0.5cm}{\rm (unit\hspace{-0.15cm}: \hspace{0.15cm}bit\hspace{0.15cm}or\hspace{0.15cm}bit/Symbol)} \hspace{0.05cm}.$$
The function is called $H_\text{bin}(p)$ the binary entropy function. The entropy of a source with a larger symbol range $M$ can often be expressed using $H_\text{bin}(p)$ .
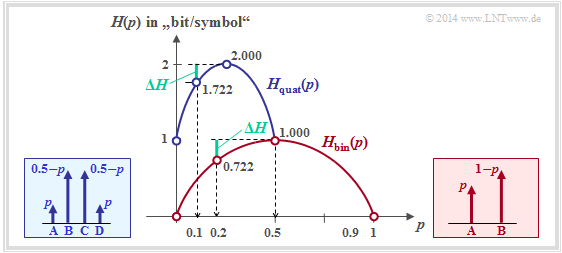
$\text{Example 2:}$ The figure shows the binary entropy function for the values $0 ≤ p ≤ 1$ of the symbol probability of $\rm A$ $($or also of $\rm B)$. You can see
- The maximum value $H_\text{max} = 1\; \rm bit$ results for $p = 0.5$, thus for equally probable binary symbols. Then $\rm A$ and $\rm B$ contribute the same amount to entropy.
- $H_\text{bin}(p)$ is symmetrical about $p = 0.5$. A source with $p_{\rm A} = 0.1$ and $p_{\rm B} = 0. 9$ has the same entropy $H = 0.469 \; \rm bit$ as a source with $p_{\rm A} = 0.9$ and $p_{\rm B} = 0.1$.
- The difference $ΔH = H_\text{max} - H$ gives the redundancy of the source and $r = ΔH/H_\text{max}$ the relative redundancy. In the example, $ΔH = 0.531\; \rm bit$ and $r = 53.1 \rm \%$.
- For $p = 0$ this results in $H = 0$, since the symbol sequence $\rm B \ B \ B \text{...}$ can be predicted with certainty. Actually, the symbol range is now only $M = 1$. The same applies to $p = 1$ ⇒ symbol sequence $\rm A \ A \ A \ text{...}$.
- $H_\text{bin}(p)$ is always a concave function, since the second derivative after the parameter $p$ is negative for all values of $p$ :
- $$\frac{ {\rm d}^2H_{\rm bin} (p)}{ {\rm d}\,p^2} = \frac{- 1}{ {\rm ln}(2) \cdot p \cdot (1-p)}< 0 \hspace{0.05cm}.$$
Message sources with a larger symbol range
In the first section of this chapter we have a quaternary message source $(M = 4)$ with the symbol probabilities $p_{\rm A} = 0. 4$, $p_{\rm B} = 0.3$, $p_{\rm C} = 0.2$ and $ p_{\rm D} = 0.1$ considered. This source has the following entropy:
- $$H_{\rm quat} = 0.4 \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{0.4} + 0.3 \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{0. 3} + 0.2 \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{0.2}+ 0.1 \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{0.1}.$$
For numerical calculation, the detour via the decimal logarithm $\lg \ x = {\rm log}_{10} \ x$ , is often necessary. Since the logarithm dualis $ {\rm log}_2 \ x$ is mostly not found on pocket calculators.
- $$H_{\rm quat}=\frac{1}{{\rm lg}\hspace{0.1cm}2} \cdot \left [ 0.4 \cdot {\rm lg}\hspace{0.1cm}\frac{1}{0.4} + 0.3 \cdot {\rm lg}\hspace{0.1cm}\frac{1}{0. 3} + 0.2 \cdot {\rm lg}\hspace{0.1cm}\frac{1}{0.2} + 0.1 \cdot {\rm lg}\hspace{0.1cm}\frac{1}{0.1} \right ] = 1.845\,{\rm bit} \hspace{0.05cm}.$$
$\text{Example 3:}$ Now there are certain symmetries between the symbol probabilities:
- $$p_{\rm A} = p_{\rm D} = p \hspace{0.05cm},\hspace{0.4cm}p_{\rm B} = p_{\rm C} = 0.5 - p \hspace{0.05cm},\hspace{0.3cm}{\rm with} \hspace{0.15cm}0 \le p \le 0.5 \hspace{0.05cm}.$$
In this case, the binary entropy function can be used to calculate the entropy:
- $$H_{\rm quat} = 2 \cdot p \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p\hspace{0.1cm} } + 2 \cdot (0.5-p) \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{0.5-p}$$
$$\Rightarrow \hspace{0.3cm} H_{\rm quat} = 1 + H_{\rm bin}(2p) \hspace{0.05cm}.$$
The graphic shows as a function of $p$
- the entropy of the quaternary source (blue)
- in comparison to the entropy course of the binary source (red).
For the quaternary source only the abscissa $0 ≤ p ≤ 0.5$ is allowed.
You can see from the blue curve for the quaternary source:
- The maximum entropy $H_\text{max} = 2 \; \rm bit/symbol$ results for $p = 0.25$ ⇒ equally probable symbols: $p_{\rm A} = p_{\rm B} = p_{\rm C} = p_{\rm A} = 0.25$.
- With $p = 0$ resp. $p = 0.5$ the quaternary source degenerates to a binary source with $p_{\rm B} = p_{\rm C} = 0. 5$ and $p_{\rm A} = p_{\rm D} = 0$ ⇒ entropy $H = 1 \; \rm bit/symbol$.
- The source with $p_{\rm A} = p_{\rm D} = 0.1$ and $p_{\rm B} = p_{\rm C} = 0.4$ has the following characteristics (each with the pseudo unit "bit/symbol"):
- (1) entropy: $H = 1 + H_{\rm bin} (2p) =1 + H_{\rm bin} (0.2) = 1.722,$
- (2) Redundancy: ${\rm \Delta }H = {\rm log_2}\hspace{0.1cm} M - H =2- 1.722= 0.278,$
- (3) relative redundancy: $r ={\rm \delta }H/({\rm log_2}\hspace{0.1cm} M) = 0.139\hspace{0.05cm}.$
- The redundancy of the quaternary source with $p = 0.1$ is equal to $ΔH = 0.278 \; \rm bit/symbol$ and thus exactly the same as the redundancy of the binary source with $p = 0.2$.
Exercises for the chapter
Exercise 1.1: Entropy of the Weather
Aufgabe 1.1Z: Binäre Entropiefunktion
Aufgabe 1.2: Entropie von Ternärquellen
List of sources
- ↑ Shannon, C.E.: A Mathematical Theory of Communication. In: Bell Syst. Techn. J. 27 (1948), pp. 379-423 and pp. 623-656.