Difference between revisions of "Information Theory/Discrete Memoryless Sources"
| Line 6: | Line 6: | ||
}} | }} | ||
| − | == # | + | == # OVERVIEW OF THE FIRST MAIN CHAPTER # == |
<br> | <br> | ||
| − | + | This first chapter describes the calculation and the meaning of entropy. According to the Shannonian information definition, entropy is a measure of the mean uncertainty about the outcome of a statistical event or the uncertainty in the measurement of a stochastic quantity. Somewhat casually expressed, the entropy of a random quantity quantifies its "randomness". | |
| − | + | In detail are discussed: | |
| − | * | + | *the ''decision content'' and the ''entropy'' of a memoryless news source, |
| − | * | + | *the ''binary entropy function'' and its application to ''non-binary sources'', |
| − | * | + | *the entropy calculation for ''memory sources'' and suitable approximations, |
| − | * | + | *the peculiarities of ''Markov sources'' regarding the entropy calculation, |
| − | * | + | *the procedure for sources with a large number of symbols, for example ''natural texts'', |
| − | * | + | *the ''entropy estimates'' according to Shannon and Küpfmüller. |
| − | + | Further information on the topic as well as Exercises, simulations and programming exercises can be found in the experiment "Value Discrete Information Theory" of the practical course "Simulation Digitaler Übertragungssysteme" (english: Simulation of Digital Transmission Systems). This (former) LNT course at the TU Munich is based on | |
| − | * | + | *the Windows program [http://en.lntwww.de/downloads/Sonstiges/Programme/WDIT.zip WDIT] ⇒ the link points to the ZIP version of the program and |
| − | * | + | *the associated [http://en.lntwww.de/downloads/Sonstiges/Texte/Wertdiskrete_Informationstheorie.pdf Internship guide] ⇒ the link refers to the PDF version. |
| − | == | + | == Model and requirements == |
<br> | <br> | ||
| − | + | We consider a value discrete message source $\rm Q$, which gives a sequence $ \langle q_ν \rangle$ of symbols. | |
| − | * | + | *For the run variable $ν = 1$, ... , $N$, where $N$ should be "sufficiently large". |
| − | * | + | *Each individual source symbol $q_ν$ comes from a symbol set $\{q_μ \}$ where $μ = 1$, ... , $M$, where $M$ denotes the symbol range: |
| − | :$$q_{\nu} \in \left \{ q_{\mu} \right \}, \hspace{0.25cm}{\rm | + | :$$q_{\nu} \in \left \{ q_{\mu} \right \}, \hspace{0.25cm}{\rm with}\hspace{0.25cm} \nu = 1, \hspace{0.05cm} \text{ ...}\hspace{0.05cm} , N\hspace{0.25cm}{\rm and}\hspace{0.25cm}\mu = 1,\hspace{0.05cm} \text{ ...}\hspace{0.05cm} , M \hspace{0.05cm}.$$ |
| − | + | The figure shows a quaternary message source $(M = 4)$ with the alphabet $\rm \{A, \ B, \ C, \ D\}$ and an exemplary sequence of length $N = 100$. | |
| − | [[File: | + | [[File:P_ID2227__Inf_T_1_1_S1a_new.png|frame|Memoryless Quaternary Message Source]] |
| − | + | The following requirements apply: | |
| − | * | + | *The quaternary news source is fully described by $M = 4$ symbol probabilities $p_μ$. In general it applies: |
| − | :$$\sum_{\mu = 1}^M \hspace{0.1cm}p_{\mu} | + | :$$\sum_{\mu = 1}^M \hspace{0.1cm}p_{\mu} = 1 \hspace{0.05cm}.$$ |
| − | * | + | *The message source is memoryless, i.e., the individual sequence elements are [[Theory_of_Stochastic_Signals/Statistical Dependence and Independence#General_definition_of_statistical_dependence|statistically independent of each other]]: |
| − | :$${\rm Pr} \left (q_{\nu} = | + | :$${\rm Pr} \left (q_{\nu} = q_{\mu} \right ) = {\rm Pr} \left (q_{\nu} = q_{\mu} \hspace{0.03cm} | \hspace{0.03cm} q_{\nu -1}, q_{\nu -2}, \hspace{0.05cm} \text{ ...}\hspace{0.05cm}\right ) \hspace{0.05cm}.$$ |
| − | * | + | *Since the alphabet consists of symbols (and not of random variables) , the specification of [[Theory_of_Stochastic_Signals/Expected_Values_and_Moments|Expected_values]] (linear mean, quadratic mean, dispersion, etc.) is not possible here, but also not necessary from an information-theoretical point of view. |
| − | + | These properties will now be illustrated with an example. | |
| − | [[File:Inf_T_1_1_S1b_vers2.png|right|frame|Relative | + | [[File:Inf_T_1_1_S1b_vers2.png|right|frame|Relative frequencies as a function of $N$]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 1:}$ |
| − | + | For the symbol probabilities of a quaternary source applies: | |
:$$p_{\rm A} = 0.4 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.3 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.2 \hspace{0.05cm},\hspace{0.2cm} | :$$p_{\rm A} = 0.4 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.3 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.2 \hspace{0.05cm},\hspace{0.2cm} | ||
p_{\rm D} = 0.1\hspace{0.05cm}.$$ | p_{\rm D} = 0.1\hspace{0.05cm}.$$ | ||
| − | + | For an infinitely long sequence $(N \to \infty)$ | |
| − | * | + | *were the [[Theory_of_Stochastic_Signals/From_Random_Experiment_to_Random_Size#Bernoulli's_Law_of_Large_Numbers|relative frequencies]] $h_{\rm A}$, $h_{\rm B}$, $h_{\rm C}$, $h_{\rm D}$ ⇒ a-posteriori parameters |
| − | * | + | *identical with the [[Theory_of_Stochastic_Signals/Some_basic_definitions#Event_and_Event_set|probabilities]] $p_{\rm A}$, $p_{\rm B}$, $p_{\rm C}$, $p_{\rm D}$ ⇒ a-priori parameters. |
| − | + | With smaller $N$ deviations may occur, as the adjacent table (result of a simulation) shows. | |
| − | *In | + | *In the graphic above an exemplary sequence is shown with $N = 100$ symbols. |
| − | * | + | *Due to the set elements $\rm A$, $\rm B$, $\rm C$ and $\rm D$ no mean values can be given. |
| − | + | However, if you replace the symbols with numerical values, for example $\rm A \Rightarrow 1$, $\rm B \Rightarrow 2$, $\rm C \Rightarrow 3$, $\rm D \Rightarrow 4$, then you will get <br> time averaging ⇒ crossing line or coulter averaging ⇒ expected value formation | |
| − | * | + | *for the [[Theory_of_Stochastic_Signals/Moments of a Discrete Random Variable#Linear_Average_-_Direct_Component|Linear_Average]] : |
| − | :$$m_1 = \overline { q_{\nu} } = {\rm E} \big [ q_{\mu} | + | :$$m_1 = \overline { q_{\nu} } = {\rm E} \big [ q_{\mu} \big ] = 0.4 \cdot 1 + 0.3 \cdot 2 + 0.2 \cdot 3 + 0.1 \cdot 4 |
= 2 \hspace{0.05cm},$$ | = 2 \hspace{0.05cm},$$ | ||
| − | * | + | *for the [[Theory_of_Stochastic_Signals/Moments of a Discrete Random Variable#Square_mean_.E2.80.93_Variance_.E2.80.93_Scattering |square mean]]: |
| − | :$$m_2 = \overline { q_{\nu}^{\hspace{0.05cm}2} } = {\rm E} \big [ q_{\mu}^{\hspace{0.05cm}2} | + | :$$m_2 = \overline { q_{\nu}^{\hspace{0.05cm}2} } = {\rm E} \big [ q_{\mu}^{\hspace{0.05cm}2} \big ] = 0.4 \cdot 1^2 + 0.3 \cdot 2^2 + 0.2 \cdot 3^2 + 0.1 \cdot 4^2 |
= 5 \hspace{0.05cm},$$ | = 5 \hspace{0.05cm},$$ | ||
| − | * | + | *for the [[Theory_of_Stochastic_Signals/Expected_Values_and_Moments#Some_often_used_Central_Moments|Standard Deviation]] (scattering) according to the "Theorem of Steiner": |
:$$\sigma = \sqrt {m_2 - m_1^2} = \sqrt {5 - 2^2} = 1 \hspace{0.05cm}.$$}} | :$$\sigma = \sqrt {m_2 - m_1^2} = \sqrt {5 - 2^2} = 1 \hspace{0.05cm}.$$}} | ||
| − | == | + | ==Decision content - Message content== |
<br> | <br> | ||
| − | [https://de.wikipedia.org/wiki/Claude_Shannon Claude Elwood Shannon] | + | [https://de.wikipedia.org/wiki/Claude_Shannon Claude Elwood Shannon] defined in 1948 in the standard work of information theory [Sha48]<ref name='Sha48'>Shannon, C.E.: A Mathematical Theory of Communication. In: Bell Syst. Techn. J. 27 (1948), pp. 379-423 and pp. 623-656.</ref> the concept of information as "decrease of uncertainty about the occurrence of a statistical event". |
| − | + | Let us make a mental experiment with $M$ possible results, which are all equally probable: $p_1 = p_2 = \hspace{0.05cm} \text{ ...}\hspace{0.05cm} = p_M = 1/M \hspace{0.05cm}.$ | |
| − | + | Under this assumption applies: | |
| − | * | + | *Is $M = 1$, then each individual attempt will yield the same result and therefore there is no uncertainty about the output. |
| − | * | + | *On the other hand, an observer learns about an experiment with $M = 2$, for example the "coin toss" with the set of events $\big \{\rm \bold symbol{\rm Z}(ahl), \rm \bold symbol{\rm W}(app) \big \}$ and the probabilities $p_{\rm Z} = p_{\rm W} = 0. 5$, a gain in information; The uncertainty regarding $\rm Z$ resp. $\rm W$ is resolved. |
| − | * | + | *In the experiment "dice" $(M = 6)$ and even more in roulette $(M = 37)$ the gained information is even more significant for the observer than in the "coin toss" when he learns which number was thrown or which ball fell. |
| − | * | + | *Finally it should be considered that the experiment "triple coin toss" with the $M = 8$ possible results $\rm ZZZ$, $\rm ZZW$, $\rm ZWZ$, $\rm ZWW$, $\rm WZZ$, $\rm WZW$, $\rm WWZ$, $\rm WWW$ provides three times the information as the single coin toss $(M = 2)$. |
| − | + | The following definition fulfills all the requirements listed here for a quantitative information measure for equally probable events, indicated only by the symbol range $M$. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ The '''decision content''' of a message source depends only on the symbol range $M$ and results in |
| − | :$$H_0 = {\rm log}\hspace{0.1cm}M = {\rm log}_2\hspace{0.1cm}M \hspace{0.15cm} {\rm (in \ | + | :$$H_0 = {\rm log}\hspace{0.1cm}M = {\rm log}_2\hspace{0.1cm}M \hspace{0.15cm} {\rm (in \ "bit")} |
= {\rm ln}\hspace{0.1cm}M \hspace{0.15cm}\text {(in "nat")} | = {\rm ln}\hspace{0.1cm}M \hspace{0.15cm}\text {(in "nat")} | ||
= {\rm lg}\hspace{0.1cm}M \hspace{0.15cm}\text {(in "Hartley")}\hspace{0.05cm}.$$ | = {\rm lg}\hspace{0.1cm}M \hspace{0.15cm}\text {(in "Hartley")}\hspace{0.05cm}.$$ | ||
| − | * | + | *The term ''message content'' is also commonly used for this. |
| − | * | + | *Since $H_0$ indicates the maximum value of the [[Information_Theory/Memory_Message_Sources#Information_content_and_Entropy|Entropy]] $H$ , $H_\text{max}$ is also used in our tutorial as short notation . }} |
| − | + | Please note our nomenclature: | |
| − | * | + | *The logarithm will be called "log" in the following, independent of the base. |
| − | * | + | *The relations mentioned above are fulfilled due to the following properties: |
| − | :$${\rm log}\hspace{0.1cm}1 = 0 | + | :$${\rm log}\hspace{0.1cm}1 = 0 \hspace{0.05cm},\hspace{0.2cm} |
{\rm log}\hspace{0.1cm}37 > {\rm log}\hspace{0.1cm}6 > {\rm log}\hspace{0.1cm}2\hspace{0.05cm},\hspace{0.2cm} | {\rm log}\hspace{0.1cm}37 > {\rm log}\hspace{0.1cm}6 > {\rm log}\hspace{0.1cm}2\hspace{0.05cm},\hspace{0.2cm} | ||
{\rm log}\hspace{0.1cm}M^k = k \cdot {\rm log}\hspace{0.1cm}M \hspace{0.05cm}.$$ | {\rm log}\hspace{0.1cm}M^k = k \cdot {\rm log}\hspace{0.1cm}M \hspace{0.05cm}.$$ | ||
| − | * | + | * Usually we use the logarithm to the base $2$ ⇒ ''Logarithm dualis'' $\rm (ld)$, where the pseudo unit "bit", more precisely: "bit/symbol", is then added: |
:$${\rm ld}\hspace{0.1cm}M = {\rm log_2}\hspace{0.1cm}M = \frac{{\rm lg}\hspace{0.1cm}M}{{\rm lg}\hspace{0.1cm}2} | :$${\rm ld}\hspace{0.1cm}M = {\rm log_2}\hspace{0.1cm}M = \frac{{\rm lg}\hspace{0.1cm}M}{{\rm lg}\hspace{0.1cm}2} | ||
| Line 118: | Line 118: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *In addition, you can find in the literature some additional definitions, which are based on the natural logarithm $\rm (ln)$ or the logarithm $\rm (lg)$ . |
==Informationsgehalt und Entropie == | ==Informationsgehalt und Entropie == | ||
Revision as of 23:55, 27 October 2020
Contents
# OVERVIEW OF THE FIRST MAIN CHAPTER #
This first chapter describes the calculation and the meaning of entropy. According to the Shannonian information definition, entropy is a measure of the mean uncertainty about the outcome of a statistical event or the uncertainty in the measurement of a stochastic quantity. Somewhat casually expressed, the entropy of a random quantity quantifies its "randomness".
In detail are discussed:
- the decision content and the entropy of a memoryless news source,
- the binary entropy function and its application to non-binary sources,
- the entropy calculation for memory sources and suitable approximations,
- the peculiarities of Markov sources regarding the entropy calculation,
- the procedure for sources with a large number of symbols, for example natural texts,
- the entropy estimates according to Shannon and Küpfmüller.
Further information on the topic as well as Exercises, simulations and programming exercises can be found in the experiment "Value Discrete Information Theory" of the practical course "Simulation Digitaler Übertragungssysteme" (english: Simulation of Digital Transmission Systems). This (former) LNT course at the TU Munich is based on
- the Windows program WDIT ⇒ the link points to the ZIP version of the program and
- the associated Internship guide ⇒ the link refers to the PDF version.
Model and requirements
We consider a value discrete message source $\rm Q$, which gives a sequence $ \langle q_ν \rangle$ of symbols.
- For the run variable $ν = 1$, ... , $N$, where $N$ should be "sufficiently large".
- Each individual source symbol $q_ν$ comes from a symbol set $\{q_μ \}$ where $μ = 1$, ... , $M$, where $M$ denotes the symbol range:
- $$q_{\nu} \in \left \{ q_{\mu} \right \}, \hspace{0.25cm}{\rm with}\hspace{0.25cm} \nu = 1, \hspace{0.05cm} \text{ ...}\hspace{0.05cm} , N\hspace{0.25cm}{\rm and}\hspace{0.25cm}\mu = 1,\hspace{0.05cm} \text{ ...}\hspace{0.05cm} , M \hspace{0.05cm}.$$
The figure shows a quaternary message source $(M = 4)$ with the alphabet $\rm \{A, \ B, \ C, \ D\}$ and an exemplary sequence of length $N = 100$.
The following requirements apply:
- The quaternary news source is fully described by $M = 4$ symbol probabilities $p_μ$. In general it applies:
- $$\sum_{\mu = 1}^M \hspace{0.1cm}p_{\mu} = 1 \hspace{0.05cm}.$$
- The message source is memoryless, i.e., the individual sequence elements are statistically independent of each other:
- $${\rm Pr} \left (q_{\nu} = q_{\mu} \right ) = {\rm Pr} \left (q_{\nu} = q_{\mu} \hspace{0.03cm} | \hspace{0.03cm} q_{\nu -1}, q_{\nu -2}, \hspace{0.05cm} \text{ ...}\hspace{0.05cm}\right ) \hspace{0.05cm}.$$
- Since the alphabet consists of symbols (and not of random variables) , the specification of Expected_values (linear mean, quadratic mean, dispersion, etc.) is not possible here, but also not necessary from an information-theoretical point of view.
These properties will now be illustrated with an example.
$\text{Example 1:}$ For the symbol probabilities of a quaternary source applies:
- $$p_{\rm A} = 0.4 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.3 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.2 \hspace{0.05cm},\hspace{0.2cm} p_{\rm D} = 0.1\hspace{0.05cm}.$$
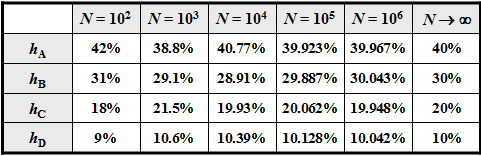
For an infinitely long sequence $(N \to \infty)$
- were the relative frequencies $h_{\rm A}$, $h_{\rm B}$, $h_{\rm C}$, $h_{\rm D}$ ⇒ a-posteriori parameters
- identical with the probabilities $p_{\rm A}$, $p_{\rm B}$, $p_{\rm C}$, $p_{\rm D}$ ⇒ a-priori parameters.
With smaller $N$ deviations may occur, as the adjacent table (result of a simulation) shows.
- In the graphic above an exemplary sequence is shown with $N = 100$ symbols.
- Due to the set elements $\rm A$, $\rm B$, $\rm C$ and $\rm D$ no mean values can be given.
However, if you replace the symbols with numerical values, for example $\rm A \Rightarrow 1$, $\rm B \Rightarrow 2$, $\rm C \Rightarrow 3$, $\rm D \Rightarrow 4$, then you will get
time averaging ⇒ crossing line or coulter averaging ⇒ expected value formation
- for the Linear_Average :
- $$m_1 = \overline { q_{\nu} } = {\rm E} \big [ q_{\mu} \big ] = 0.4 \cdot 1 + 0.3 \cdot 2 + 0.2 \cdot 3 + 0.1 \cdot 4 = 2 \hspace{0.05cm},$$
- for the square mean:
- $$m_2 = \overline { q_{\nu}^{\hspace{0.05cm}2} } = {\rm E} \big [ q_{\mu}^{\hspace{0.05cm}2} \big ] = 0.4 \cdot 1^2 + 0.3 \cdot 2^2 + 0.2 \cdot 3^2 + 0.1 \cdot 4^2 = 5 \hspace{0.05cm},$$
- for the Standard Deviation (scattering) according to the "Theorem of Steiner":
- $$\sigma = \sqrt {m_2 - m_1^2} = \sqrt {5 - 2^2} = 1 \hspace{0.05cm}.$$
Decision content - Message content
Claude Elwood Shannon defined in 1948 in the standard work of information theory [Sha48][1] the concept of information as "decrease of uncertainty about the occurrence of a statistical event".
Let us make a mental experiment with $M$ possible results, which are all equally probable: $p_1 = p_2 = \hspace{0.05cm} \text{ ...}\hspace{0.05cm} = p_M = 1/M \hspace{0.05cm}.$
Under this assumption applies:
- Is $M = 1$, then each individual attempt will yield the same result and therefore there is no uncertainty about the output.
- On the other hand, an observer learns about an experiment with $M = 2$, for example the "coin toss" with the set of events $\big \{\rm \bold symbol{\rm Z}(ahl), \rm \bold symbol{\rm W}(app) \big \}$ and the probabilities $p_{\rm Z} = p_{\rm W} = 0. 5$, a gain in information; The uncertainty regarding $\rm Z$ resp. $\rm W$ is resolved.
- In the experiment "dice" $(M = 6)$ and even more in roulette $(M = 37)$ the gained information is even more significant for the observer than in the "coin toss" when he learns which number was thrown or which ball fell.
- Finally it should be considered that the experiment "triple coin toss" with the $M = 8$ possible results $\rm ZZZ$, $\rm ZZW$, $\rm ZWZ$, $\rm ZWW$, $\rm WZZ$, $\rm WZW$, $\rm WWZ$, $\rm WWW$ provides three times the information as the single coin toss $(M = 2)$.
The following definition fulfills all the requirements listed here for a quantitative information measure for equally probable events, indicated only by the symbol range $M$.
$\text{Definition:}$ The decision content of a message source depends only on the symbol range $M$ and results in
- $$H_0 = {\rm log}\hspace{0.1cm}M = {\rm log}_2\hspace{0.1cm}M \hspace{0.15cm} {\rm (in \ "bit")} = {\rm ln}\hspace{0.1cm}M \hspace{0.15cm}\text {(in "nat")} = {\rm lg}\hspace{0.1cm}M \hspace{0.15cm}\text {(in "Hartley")}\hspace{0.05cm}.$$
- The term message content is also commonly used for this.
- Since $H_0$ indicates the maximum value of the Entropy $H$ , $H_\text{max}$ is also used in our tutorial as short notation .
Please note our nomenclature:
- The logarithm will be called "log" in the following, independent of the base.
- The relations mentioned above are fulfilled due to the following properties:
- $${\rm log}\hspace{0.1cm}1 = 0 \hspace{0.05cm},\hspace{0.2cm} {\rm log}\hspace{0.1cm}37 > {\rm log}\hspace{0.1cm}6 > {\rm log}\hspace{0.1cm}2\hspace{0.05cm},\hspace{0.2cm} {\rm log}\hspace{0.1cm}M^k = k \cdot {\rm log}\hspace{0.1cm}M \hspace{0.05cm}.$$
- Usually we use the logarithm to the base $2$ ⇒ Logarithm dualis $\rm (ld)$, where the pseudo unit "bit", more precisely: "bit/symbol", is then added:
- $${\rm ld}\hspace{0.1cm}M = {\rm log_2}\hspace{0.1cm}M = \frac{{\rm lg}\hspace{0.1cm}M}{{\rm lg}\hspace{0.1cm}2} = \frac{{\rm ln}\hspace{0.1cm}M}{{\rm ln}\hspace{0.1cm}2} \hspace{0.05cm}.$$
- In addition, you can find in the literature some additional definitions, which are based on the natural logarithm $\rm (ln)$ or the logarithm $\rm (lg)$ .
Informationsgehalt und Entropie
Wir verzichten nun auf die bisherige Voraussetzung, dass alle $M$ möglichen Ergebnisse eines Versuchs gleichwahrscheinlich seien. Im Hinblick auf eine möglichst kompakte Schreibweise legen wir für diese Seite lediglich fest:
- $$p_1 > p_2 > \hspace{0.05cm} \text{ ...}\hspace{0.05cm} > p_\mu > \hspace{0.05cm} \text{ ...}\hspace{0.05cm} > p_{M-1} > p_M\hspace{0.05cm},\hspace{0.4cm}\sum_{\mu = 1}^M p_{\mu} = 1 \hspace{0.05cm}.$$
Wir betrachten nun den Informationsgehalt der einzelnen Symbole, wobei wir den „Logarithmus dualis” mit $\log_2$ bezeichnen:
- $$I_\mu = {\rm log_2}\hspace{0.1cm}\frac{1}{p_\mu}= -\hspace{0.05cm}{\rm log_2}\hspace{0.1cm}{p_\mu} \hspace{0.5cm}{\rm (Einheit\hspace{-0.15cm}: \hspace{0.15cm}bit\hspace{0.15cm}oder\hspace{0.15cm}bit/Symbol)} \hspace{0.05cm}.$$
Man erkennt:
- Wegen $p_μ ≤ 1$ ist der Informationsgehalt nie negativ. Im Grenzfall $p_μ \to 1$ geht $I_μ \to 0$.
- Allerdings ist für $I_μ = 0$ ⇒ $p_μ = 1$ ⇒ $M = 1$ auch der Entscheidungsgehalt $H_0 = 0$.
- Bei abfallenden Wahrscheinlichkeiten $p_μ$ nimmt der Informationsgehalt kontinuierlich zu:
- $$I_1 < I_2 < \hspace{0.05cm} \text{ ...}\hspace{0.05cm} < I_\mu <\hspace{0.05cm} \text{ ...}\hspace{0.05cm} < I_{M-1} < I_M \hspace{0.05cm}.$$
$\text{Fazit:}$ Je unwahrscheinlicher ein Ereignis ist, desto größer ist sein Informationsgehalt. Diesen Sachverhalt stellt man auch im täglichen Leben fest:
- „6 Richtige” im Lotto nimmt man sicher eher wahr als „3 Richtige” oder gar keinen Gewinn.
- Ein Tsunami in Asien dominiert auch die Nachrichten in Deutschland über Wochen im Gegensatz zu den fast standardmäßigen Verspätungen der Deutschen Bahn.
- Eine Niederlagenserie von Bayern München führt zu Riesen–Schlagzeilen im Gegensatz zu einer Siegesserie. Bei 1860 München ist genau das Gegenteil der Fall.
Der Informationsgehalt eines einzelnen Symbols (oder Ereignisses) ist allerdings nicht sehr interessant. Dagegen erhält man
- durch Scharmittelung über alle möglichen Symbole $q_μ$ bzw.
- durch Zeitmittelung über alle Elemente der Folge $\langle q_ν \rangle$
eine der zentralen Größen der Informationstheorie.
$\text{Definition:}$ Die Entropie $H$ einer Quelle gibt den mittleren Informationsgehalt aller Symbole an:
- $$H = \overline{I_\nu} = {\rm E}\hspace{0.01cm}[I_\mu] = \sum_{\mu = 1}^M p_{\mu} \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{p_\mu}= -\sum_{\mu = 1}^M p_{\mu} \cdot{\rm log_2}\hspace{0.1cm}{p_\mu} \hspace{0.5cm}\text{(Einheit: bit, genauer: bit/Symbol)} \hspace{0.05cm}.$$
Die überstreichende Linie kennzeichnet wieder eine Zeitmittelung und $\rm E[\text{...}]$ eine Scharmittelung.
Die Entropie ist unter anderem ein Maß für
- die mittlere Unsicherheit über den Ausgang eines statistischen Ereignisses,
- die „Zufälligkeit” dieses Ereignisses, sowie
- den mittleren Informationsgehalt einer Zufallsgröße.
Binäre Entropiefunktion
Wir beschränken uns zunächst auf den Sonderfall $M = 2$ und betrachten eine binäre Quelle, die die beiden Symbole $\rm A$ und $\rm B$ abgibt. Die Auftrittwahrscheinlichkeiten seien $p_{\rm A} = p$ und $p_{\rm B} = 1 – p$.
Für die Entropie dieser Binärquelle gilt:
- $$H_{\rm bin} (p) = p \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p\hspace{0.1cm}} + (1-p) \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{1-p} \hspace{0.5cm}{\rm (Einheit\hspace{-0.15cm}: \hspace{0.15cm}bit\hspace{0.15cm}oder\hspace{0.15cm}bit/Symbol)} \hspace{0.05cm}.$$
Man nennt die Funktion $H_\text{bin}(p)$ die binäre Entropiefunktion. Die Entropie einer Quelle mit größerem Symbolumfang $M$ lässt sich häufig unter Verwendung von $H_\text{bin}(p)$ ausdrücken.
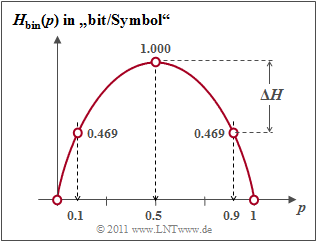
$\text{Beispiel 2:}$ Die Grafik zeigt die binäre Entropiefunktion für die Werte $0 ≤ p ≤ 1$ der Symbolwahrscheinlichkeit von $\rm A$ $($oder auch von $\rm B)$. Man erkennt:
- Der Maximalwert $H_\text{max} = 1\; \rm bit$ ergibt sich für $p = 0.5$, also für gleichwahrscheinliche Binärsymbole. Dann liefern $\rm A$ und $\rm B$ jeweils den gleichen Beitrag zur Entropie.
- $H_\text{bin}(p)$ ist symmetrisch um $p = 0.5$. Eine Quelle mit $p_{\rm A} = 0.1$ und $p_{\rm B} = 0.9$ hat die gleiche Entropie $H = 0.469 \; \rm bit$ wie eine Quelle mit $p_{\rm A} = 0.9$ und $p_{\rm B} = 0.1$.
- Die Differenz $ΔH = H_\text{max} - H$ gibt die Redundanz der Quelle an und $r = ΔH/H_\text{max}$ die relative Redundanz. Im Beispiel ergeben sich $ΔH = 0.531\; \rm bit$ bzw. $r = 53.1 \rm \%$.
- Für $p = 0$ ergibt sich $H = 0$, da hier die Symbolfolge $\rm B \ B \ B \text{...}$ mit Sicherheit vorhergesagt werden kann. Eigentlich ist nun der Symbolumfang nur noch $M = 1$. Gleiches gilt für $p = 1$ ⇒ Symbolfolge $\rm A \ A \ A \text{...}$.
- $H_\text{bin}(p)$ ist stets eine konkave Funktion, da die zweite Ableitung nach dem Parameter $p$ für alle Werte von $p$ negativ ist:
- $$\frac{ {\rm d}^2H_{\rm bin} (p)}{ {\rm d}\,p^2} = \frac{- 1}{ {\rm ln}(2) \cdot p \cdot (1-p)}< 0 \hspace{0.05cm}.$$
Nachrichtenquellen mit größerem Symbolumfang
Im ersten Abschnitt dieses Kapitels haben wir eine quaternäre Nachrichtenquelle $(M = 4)$ mit den Symbolwahrscheinlichkeiten $p_{\rm A} = 0.4$, $p_{\rm B} = 0.3$, $p_{\rm C} = 0.2$ und $ p_{\rm D} = 0.1$ betrachtet. Diese Quelle besitzt die folgende Entropie:
- $$H_{\rm quat} = 0.4 \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{0.4} + 0.3 \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{0.3} + 0.2 \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{0.2}+ 0.1 \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{0.1}.$$
Oft ist zur zahlenmäßigen Berechnung der Umweg über den Zehnerlogarithmus $\lg \ x = {\rm log}_{10} \ x$ sinnvoll, da der Logarithmus dualis $ {\rm log}_2 \ x$ meist auf Taschenrechnern nicht zu finden ist.
- $$H_{\rm quat}=\frac{1}{{\rm lg}\hspace{0.1cm}2} \cdot \left [ 0.4 \cdot {\rm lg}\hspace{0.1cm}\frac{1}{0.4} + 0.3 \cdot {\rm lg}\hspace{0.1cm}\frac{1}{0.3} + 0.2 \cdot {\rm lg}\hspace{0.1cm}\frac{1}{0.2}+ 0.1 \cdot {\rm lg}\hspace{0.1cm}\frac{1}{0.1} \right ] = 1.845\,{\rm bit} \hspace{0.05cm}.$$
$\text{Beispiel 3:}$ Nun bestehen zwischen den einzelnen Symbolwahrscheinlichkeiten gewisse Symmetrien:
- $$p_{\rm A} = p_{\rm D} = p \hspace{0.05cm},\hspace{0.4cm}p_{\rm B} = p_{\rm C} = 0.5 - p \hspace{0.05cm},\hspace{0.3cm}{\rm mit} \hspace{0.15cm}0 \le p \le 0.5 \hspace{0.05cm}.$$
In diesem Fall kann zur Entropieberechnung auf die binäre Entropiefunktion zurückgegriffen werden:
- $$H_{\rm quat} = 2 \cdot p \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p\hspace{0.1cm} } + 2 \cdot (0.5-p) \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{0.5-p}$$
- $$\Rightarrow \hspace{0.3cm} H_{\rm quat} = 1 + H_{\rm bin}(2p) \hspace{0.05cm}.$$
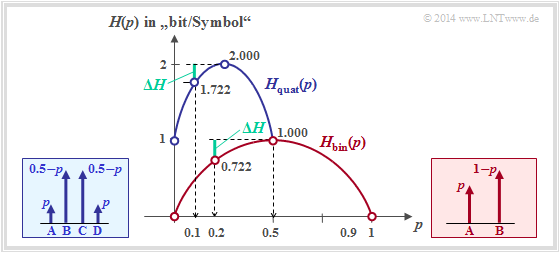
Die Grafik zeigt abhängig von $p$
- den Entropieverlauf der Quaternärquelle (blau)
- im Vergleich zum Entropieverlauf der Binärquelle (rot).
Für die Quaternärquelle ist nur der Abszissen $0 ≤ p ≤ 0.5$ zulässig.
Man erkennt aus der blauen Kurve für die Quaternärquelle:
- Die maximale Entropie $H_\text{max} = 2 \; \rm bit/Symbol$ ergibt sich für $p = 0.25$ ⇒ gleichwahrscheinliche Symbole: $p_{\rm A} = p_{\rm B} = p_{\rm C} = p_{\rm A} = 0.25$.
- Mit $p = 0$ bzw. $p = 0.5$ entartet die Quaternärquelle zu einer Binärquelle mit $p_{\rm B} = p_{\rm C} = 0.5$ und $p_{\rm A} = p_{\rm D} = 0$ ⇒ Entropie $H = 1 \; \rm bit/Symbol$.
- Die Quelle mit $p_{\rm A} = p_{\rm D} = 0.1$ und $p_{\rm B} = p_{\rm C} = 0.4$ weist folgende Kennwerte auf (jeweils mit der Pseudoeinheit „bit/Symbol”):
- (1) Entropie: $H = 1 + H_{\rm bin} (2p) =1 + H_{\rm bin} (0.2) = 1.722,$
- (2) Redundanz: ${\rm \Delta }H = {\rm log_2}\hspace{0.1cm} M - H =2- 1.722= 0.278,$
- (3) relative Redundanz: $r ={\rm \Delta }H/({\rm log_2}\hspace{0.1cm} M) = 0.139\hspace{0.05cm}.$
- Die Redundanz der Quaternärquelle mit $p = 0.1$ ist gleich $ΔH = 0.278 \; \rm bit/Symbol$ und damit genau so groß wie die Redundanz der Binärquelle mit $p = 0.2$.
Aufgaben zum Kapitel
Aufgabe 1.1Z: Binäre Entropiefunktion
Aufgabe 1.2: Entropie von Ternärquellen
Quellenverzeichnis
- ↑ Shannon, C.E.: A Mathematical Theory of Communication. In: Bell Syst. Techn. J. 27 (1948), pp. 379-423 and pp. 623-656.