Difference between revisions of "Information Theory/Discrete Sources with Memory"
| (31 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Entropy of Discrete Sources |
| − | |Vorherige Seite= | + | |Vorherige Seite=Discrete Memoryless Sources |
| − | |Nächste Seite= | + | |Nächste Seite=Natural Discrete Sources |
}} | }} | ||
| Line 10: | Line 10: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Example 1:}$ | $\text{Example 1:}$ | ||
| − | At the [[Information_Theory/Discrete Memoryless Sources#Model_and_requirements|beginning of the first chapter]] we have considered a memoryless message source with the symbol set $\rm \{A, \ B, \ C, \ D\}$ ⇒ $M = 4$ . An exemplary symbol sequence is shown again in the following figure as source $\rm Q1$ . | + | At the [[Information_Theory/Discrete Memoryless Sources#Model_and_requirements|"beginning of the first chapter"]] we have considered a memoryless message source with the symbol set $\rm \{A, \ B, \ C, \ D\}$ ⇒ $M = 4$ . An exemplary symbol sequence is shown again in the following figure as source $\rm Q1$ . |
| − | With the symbol probabilities $p_{\rm A} = 0.4 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.3 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.2 \hspace{0.05cm},\hspace{0.2cm} | + | *With the symbol probabilities $p_{\rm A} = 0.4 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.3 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.2 \hspace{0.05cm},\hspace{0.2cm} |
p_{\rm D} = 0.1\hspace{0.05cm}$ the entropy is | p_{\rm D} = 0.1\hspace{0.05cm}$ the entropy is | ||
| Line 18: | Line 18: | ||
\hspace{0.01cm}.$$ | \hspace{0.01cm}.$$ | ||
| − | Due to the unequal symbol probabilities the entropy is smaller than | + | *Due to the unequal symbol probabilities the entropy is smaller than $H_0 = \log_2 M = 2 \hspace{0.05cm} \rm bit/symbol$. |
[[File:EN_Inf_T_1_2_S1a.png|right|frame|Quaternary source without/with memory]] | [[File:EN_Inf_T_1_2_S1a.png|right|frame|Quaternary source without/with memory]] | ||
| Line 32: | Line 32: | ||
$\text{Conclusion:}$ | $\text{Conclusion:}$ | ||
This example shows: | This example shows: | ||
| − | + | #The entropy of a source with memory is smaller than the entropy of a memoryless source with equal symbol probabilities. | |
| − | + | #The statistical bindings within the sequence $〈 q_ν 〉$ have to be considered now, | |
| − | + | #namely the dependency of the symbol $q_ν$ from the predecessor symbols $q_{ν-1}$, $q_{ν-2}$, ... }} | |
| Line 40: | Line 40: | ||
<br> | <br> | ||
We continue to look at the source symbol sequence $〈 q_1, \hspace{0.05cm} q_2,\hspace{0.05cm}\text{ ...} \hspace{0.05cm}, q_{ν-1}, \hspace{0.05cm}q_ν, \hspace{0.05cm}\hspace{0.05cm}q_{ν+1} .\hspace{0.05cm}\text{...} \hspace{0.05cm}〉$ and now consider the entropy of two successive source symbols. | We continue to look at the source symbol sequence $〈 q_1, \hspace{0.05cm} q_2,\hspace{0.05cm}\text{ ...} \hspace{0.05cm}, q_{ν-1}, \hspace{0.05cm}q_ν, \hspace{0.05cm}\hspace{0.05cm}q_{ν+1} .\hspace{0.05cm}\text{...} \hspace{0.05cm}〉$ and now consider the entropy of two successive source symbols. | ||
| − | *All source symbols $q_ν$ are taken from an alphabet with the symbol set size $M$, so that for the combination $(q_ν, \hspace{0.05cm}q_{ν+1})$ there are exactly $M^2$ possible symbol pairs with the following [[Theory_of_Stochastic_Signals/ | + | *All source symbols $q_ν$ are taken from an alphabet with the symbol set size $M$, so that for the combination $(q_ν, \hspace{0.05cm}q_{ν+1})$ there are exactly $M^2$ possible symbol pairs with the following [[Theory_of_Stochastic_Signals/Set_Theory_Basics#Intersection_set|"combined probabilities"]]: |
:$${\rm Pr}(q_{\nu}\cap q_{\nu+1})\le {\rm Pr}(q_{\nu}) \cdot {\rm Pr}( q_{\nu+1}) | :$${\rm Pr}(q_{\nu}\cap q_{\nu+1})\le {\rm Pr}(q_{\nu}) \cdot {\rm Pr}( q_{\nu+1}) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *From this, the '''compound entropy''' of two consecutive symbols can be computed: | + | *From this, the »'''compound entropy'''« of two consecutive symbols can be computed: |
:$$H_2\hspace{0.05cm}' = \sum_{q_{\nu}\hspace{0.05cm} \in \hspace{0.05cm}\{ \hspace{0.05cm}q_{\mu}\hspace{0.01cm} \}} \ \sum_{q_{\nu+1}\hspace{0.05cm} \in \hspace{0.05cm}\{ \hspace{0.05cm} q_{\mu}\hspace{0.01cm} \}}\hspace{-0.1cm}{\rm Pr}(q_{\nu}\cap q_{\nu+1}) \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{{\rm Pr}(q_{\nu}\cap q_{\nu+1})} \hspace{0.4cm}({\rm unit\hspace{-0.1cm}: \hspace{0.1cm}bit/two–tuple}) | :$$H_2\hspace{0.05cm}' = \sum_{q_{\nu}\hspace{0.05cm} \in \hspace{0.05cm}\{ \hspace{0.05cm}q_{\mu}\hspace{0.01cm} \}} \ \sum_{q_{\nu+1}\hspace{0.05cm} \in \hspace{0.05cm}\{ \hspace{0.05cm} q_{\mu}\hspace{0.01cm} \}}\hspace{-0.1cm}{\rm Pr}(q_{\nu}\cap q_{\nu+1}) \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{{\rm Pr}(q_{\nu}\cap q_{\nu+1})} \hspace{0.4cm}({\rm unit\hspace{-0.1cm}: \hspace{0.1cm}bit/two–tuple}) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | :The index "2" symbolizes that the entropy thus calculated refers to '''two-tuples'''. | + | :The index "2" symbolizes that the entropy thus calculated refers to »'''two-tuples'''«. |
*To get the average information content per symbol, $H_2\hspace{0.05cm}'$ has to be divided in half: | *To get the average information content per symbol, $H_2\hspace{0.05cm}'$ has to be divided in half: | ||
| Line 57: | Line 57: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *In order to achieve a consistent nomenclature, we now label the entropy defined in chapter [[Information_Theory/ | + | *In order to achieve a consistent nomenclature, we now label the entropy defined in chapter [[Information_Theory/Discrete_Memoryless_Sources#Model_and_requirements|"Memoryless Message Sources"]] with $H_1$: |
:$$H_1 = \sum_{q_{\nu}\hspace{0.05cm} \in \hspace{0.05cm}\{ \hspace{0.05cm}q_{\mu}\hspace{0.01cm} \}} {\rm Pr}(q_{\nu}) \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{{\rm Pr}(q_{\nu})} \hspace{0.5cm}({\rm unit\hspace{-0.1cm}: \hspace{0.1cm}bit/symbol}) | :$$H_1 = \sum_{q_{\nu}\hspace{0.05cm} \in \hspace{0.05cm}\{ \hspace{0.05cm}q_{\mu}\hspace{0.01cm} \}} {\rm Pr}(q_{\nu}) \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{{\rm Pr}(q_{\nu})} \hspace{0.5cm}({\rm unit\hspace{-0.1cm}: \hspace{0.1cm}bit/symbol}) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *The index "1" is supposed to indicate that $H_1$ considers only the symbol probabilities and not statistical bindings between symbols within the sequence. With | + | *The index "1" is supposed to indicate that $H_1$ considers only the symbol probabilities and not statistical bindings between symbols within the sequence. With $H_0 = \log_2 \ M$ the following size relation results: |
| − | $$H_0 \ge H_1 \ge H_2 | + | :$$H_0 \ge H_1 \ge H_2 |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| Line 70: | Line 70: | ||
| − | The previous equations each indicate an "ensemble mean value". The probabilities required for the calculation of $H_1$ and $H_2$ can, however, also be calculated as time averages from a very long sequence or, more precisely, approximated by the corresponding [[Theory_of_Stochastic_Signals/ | + | The previous equations each indicate an "ensemble mean value". The probabilities required for the calculation of $H_1$ and $H_2$ can, however, also be calculated as time averages from a very long sequence or, more precisely, approximated by the corresponding [[Theory_of_Stochastic_Signals/From_Random_Experiment_to_Random_Variable#Bernoulli.27s_law_of_large_numbers|"relative frequencies"]]. |
Let us now illustrate the calculation of entropy approximations $H_1$ and $H_2$ with three examples. | Let us now illustrate the calculation of entropy approximations $H_1$ and $H_2$ with three examples. | ||
| + | [[File:Inf_T_1_2_S2_vers2.png|right|frame|Ternary symbol sequence and formation of two-tuples]] | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Example 2:}$ | $\text{Example 2:}$ | ||
| − | We will first look at the sequence $〈 q_1$, ... , $q_{50} \rangle $ according to the graphic, where the sequence elements $q_ν$ originate from the alphabet $\rm \{A, \ B, \ C \}$ ⇒ the symbol | + | We will first look at the sequence $〈 q_1$, ... , $q_{50} \rangle $ according to the graphic, where the sequence elements $q_ν$ originate from the alphabet $\rm \{A, \ B, \ C \}$ ⇒ the symbol set size is $M = 3$. |
| − | + | *By time averaging over $50$ symbols one gets the symbol probabilities $p_{\rm A} ≈ 0.5$, $p_{\rm B} ≈ 0.3$ and $p_{\rm C} ≈ 0.2$, with which one can calculate the first order entropy approximation: | |
| − | |||
| − | By time averaging over | ||
:$$H_1 = 0.5 \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{0.5} + 0.3 \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{0.3} + 0.2 \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{0.2} \approx \, 1.486 \,{\rm bit/symbol} | :$$H_1 = 0.5 \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{0.5} + 0.3 \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{0.3} + 0.2 \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{0.2} \approx \, 1.486 \,{\rm bit/symbol} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Due to the not equally probable symbols $H_1 < H_0 = 1.585 \hspace{0.05cm}. \rm bit/symbol$. As an approximation for the probabilities of two-tuples one gets from the above sequence: | + | *Due to the not equally probable symbols $H_1 < H_0 = 1.585 \hspace{0.05cm}. \rm bit/symbol$. As an approximation for the probabilities of two-tuples one gets from the above sequence: |
:$$\begin{align*}p_{\rm AA} \hspace{-0.1cm}& = \hspace{-0.1cm} 14/49\hspace{0.05cm}, \hspace{0.2cm}p_{\rm AB} = 8/49\hspace{0.05cm}, \hspace{0.2cm}p_{\rm AC} = 3/49\hspace{0.05cm}, \\\ | :$$\begin{align*}p_{\rm AA} \hspace{-0.1cm}& = \hspace{-0.1cm} 14/49\hspace{0.05cm}, \hspace{0.2cm}p_{\rm AB} = 8/49\hspace{0.05cm}, \hspace{0.2cm}p_{\rm AC} = 3/49\hspace{0.05cm}, \\\ | ||
| Line 91: | Line 90: | ||
p_{\rm CA} \hspace{-0.1cm}& = \hspace{0.07cm} 4/49\hspace{0.05cm}, \hspace{0.25cm}p_{\rm CB} = 5/49\hspace{0.05cm}, \hspace{0.2cm}p_{\rm CC} = 1/49\hspace{0.05cm}.\end{align*}$$ | p_{\rm CA} \hspace{-0.1cm}& = \hspace{0.07cm} 4/49\hspace{0.05cm}, \hspace{0.25cm}p_{\rm CB} = 5/49\hspace{0.05cm}, \hspace{0.2cm}p_{\rm CC} = 1/49\hspace{0.05cm}.\end{align*}$$ | ||
| − | Please note that the $50$ sequence elements can only be formed from $49$ two-tuples $(\rm AA$, ... , $\rm CC)$ which are marked in different colors in the graphic. | + | *Please note that the $50$ sequence elements can only be formed from $49$ two-tuples $(\rm AA$, ... , $\rm CC)$ which are marked in different colors in the graphic. |
| − | + | #The entropy approximation $H_2$ should actually be equal to $H_1$ since the given symbol sequence comes from a memoryless source. | |
| − | + | #Because of the short sequence length $N = 50$ and the resulting statistical inaccuracy, however, a smaller value results: | |
| − | :$$H_2 ≈ 1.39\hspace{0.05cm} \rm bit/symbol.$$}} | + | ::$$H_2 ≈ 1.39\hspace{0.05cm} \rm bit/symbol.$$}} |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Example 3:}$ | $\text{Example 3:}$ | ||
| − | Now let us consider a ''memoryless binary source'' with equally probable symbols, i.e. there would be $p_{\rm A} = p_{\rm B} = 1/2$. The first twenty subsequent elements are $〈 q_ν 〉 =\rm BBAAABAABBBBBAAAABABAB$ ... | + | Now let us consider a »'''memoryless binary source'''« with equally probable symbols, i.e. there would be $p_{\rm A} = p_{\rm B} = 1/2$. The first twenty subsequent elements are $〈 q_ν 〉 =\rm BBAAABAABBBBBAAAABABAB$ ... |
*Because of the equally probable binary symbols $H_1 = H_0 = 1 \hspace{0.05cm} \rm bit/symbol$. | *Because of the equally probable binary symbols $H_1 = H_0 = 1 \hspace{0.05cm} \rm bit/symbol$. | ||
| − | *The compound probability $p_{\rm AB}$ of the combination $\rm AB$ is equal to $p_{\rm A} | + | |
| + | *The compound probability $p_{\rm AB}$ of the combination $\rm AB$ is equal to $p_{\rm A} \cdot p_{\rm B} = 1/4$. Also $p_{\rm AA} = p_{\rm BB} = p_{\rm BA} = 1/4$. | ||
| + | |||
*This gives for the second entropy approximation | *This gives for the second entropy approximation | ||
| Line 108: | Line 109: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | <u>Note</u>: Due to the short length of the given sequence the probabilities are slightly different: $p_{\rm AA} = 6/19$, $p_{\rm BB} = 5/19$, $p_{\rm AB} = p_{\rm BA} = 4/19$.}} | |
| Line 115: | Line 116: | ||
The third sequence considered here results from the binary sequence of $\text{Example 3}$ by using a simple repeat code: | The third sequence considered here results from the binary sequence of $\text{Example 3}$ by using a simple repeat code: | ||
:$$〈 q_ν 〉 =\rm BbBbAaAaAaBbAaAaBbBb \text{...} $$ | :$$〈 q_ν 〉 =\rm BbBbAaAaAaBbAaAaBbBb \text{...} $$ | ||
| − | *The repeated symbols are marked by corresponding lower case letters. | + | *The repeated symbols are marked by corresponding lower case letters. But it still applies $M=2$. |
| + | |||
*Because of the equally probable binary symbols, this also results in $H_1 = H_0 = 1 \hspace{0.05cm} \rm bit/symbol$. | *Because of the equally probable binary symbols, this also results in $H_1 = H_0 = 1 \hspace{0.05cm} \rm bit/symbol$. | ||
| − | *As shown in [[Aufgaben: | + | |
| + | *As shown in [[Aufgaben:Exercise_1.3:_Entropy_Approximations|"Exercise 1.3"]] for the compound probabilities we obtain $p_{\rm AA}=p_{\rm BB} = 3/8$ and $p_{\rm AB}=p_{\rm BA} = 1/8$. Hence | ||
:$$\begin{align*}H_2 ={1}/{2} \cdot \big [ 2 \cdot {3}/{8} \cdot {\rm log}_2\hspace{0.1cm} {8}/{3} + | :$$\begin{align*}H_2 ={1}/{2} \cdot \big [ 2 \cdot {3}/{8} \cdot {\rm log}_2\hspace{0.1cm} {8}/{3} + | ||
2 \cdot {1}/{8} \cdot {\rm log}_2\hspace{0.1cm}8\big ] = {3}/{8} \cdot {\rm log}_2\hspace{0.1cm}8 - {3}/{8} \cdot{\rm log}_2\hspace{0.1cm}3 + {1}/{8} \cdot {\rm log}_2\hspace{0.1cm}8 \approx 0.906 \,{\rm bit/symbol} < H_1 = H_0 | 2 \cdot {1}/{8} \cdot {\rm log}_2\hspace{0.1cm}8\big ] = {3}/{8} \cdot {\rm log}_2\hspace{0.1cm}8 - {3}/{8} \cdot{\rm log}_2\hspace{0.1cm}3 + {1}/{8} \cdot {\rm log}_2\hspace{0.1cm}8 \approx 0.906 \,{\rm bit/symbol} < H_1 = H_0 | ||
| Line 123: | Line 126: | ||
A closer look at the task at hand leads to the following conclusion: | A closer look at the task at hand leads to the following conclusion: | ||
| − | *The entropy should actually be $H = 0.5 \hspace{0.05cm} \rm bit/symbol$ | + | *The entropy should actually be $H = 0.5 \hspace{0.05cm} \rm bit/symbol$ (every second symbol does not provide new information). |
| − | *The second entropy approximation $H_2 = 0.906 \hspace{0.05cm} \rm bit/symbol$ | + | |
| − | *For the determination | + | *The second entropy approximation $H_2 = 0.906 \hspace{0.05cm} \rm bit/symbol$ is much larger than the entropy $H$. |
| − | *In the following, such a block is referred to as $k$ | + | |
| + | *For the entropy determination, the second order approximation is not sufficient. Rather, one must consider larger contiguous blocks of $k > 2$ symbols. | ||
| + | |||
| + | *In the following, such a block is referred to as "$k$–tuple".}} | ||
==Generalization to $k$-tuple and boundary crossing == | ==Generalization to $k$-tuple and boundary crossing == | ||
<br> | <br> | ||
| − | For abbreviation we write using the compound probability $p_i^{(k)}$ a $k$ | + | For abbreviation we write using the compound probability $p_i^{(k)}$ for a $k$–tuple in general: |
| − | :$$H_k = \frac{1}{k} \cdot \sum_{i=1}^{M^k} p_i^{(k)} \cdot {\rm log}_2\hspace{0.1cm} \frac{1}{p_i^{(k)}} \hspace{0.5cm}({\rm | + | :$$H_k = \frac{1}{k} \cdot \sum_{i=1}^{M^k} p_i^{(k)} \cdot {\rm log}_2\hspace{0.1cm} \frac{1}{p_i^{(k)}} \hspace{0.5cm}({\rm unit\hspace{-0.1cm}: \hspace{0.1cm}bit/symbol}) |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | The control variable $i$ stands for one of the $M^k$ | + | *The control variable $i$ stands for one of the $M^k$ tuples. |
| + | |||
| + | *The previously calculated approximation $H_2$ results with $k = 2$. | ||
| + | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | The ''' | + | The »'''entropy of a discrete source with memory'''« has the following limit: |
:$$H = \lim_{k \rightarrow \infty }H_k \hspace{0.05cm}.$$ | :$$H = \lim_{k \rightarrow \infty }H_k \hspace{0.05cm}.$$ | ||
| − | For the ''entropy approximations'' $H_k$ the following relations apply $(H_0 | + | *For the »'''entropy approximations'''« $H_k$ the following relations apply $(H_0=\log_2 M)$: |
:$$H \le \text{...} \le H_k \le \text{...} \le H_2 \le H_1 \le H_0 \hspace{0.05cm}.$$}} | :$$H \le \text{...} \le H_k \le \text{...} \le H_2 \le H_1 \le H_0 \hspace{0.05cm}.$$}} | ||
| − | The computational effort will increase with increasing $k$ except for a few special cases (see the following example) and depends on the symbol size $M$ of course: | + | The computational effort will increase with increasing $k$ except for a few special cases (see the following example) and depends on the symbol set size $M$ of course: |
| − | *For the calculation of $H_{10}$ a binary source $(M = 2)$ | + | *For the calculation of $H_{10}$ for a binary source $(M = 2)$ one must average over $2^{10} = 1024$ terms. |
| + | |||
*With each further increase of $k$ by $1$ the number of sum terms doubles. | *With each further increase of $k$ by $1$ the number of sum terms doubles. | ||
| − | *In case of a quaternary source $(M = 4)$ it must already be averaged over $4^{10} = 1\hspace{0.08cm}048\hspace{0.08cm}576$ summation terms | + | |
| − | * Considering that each of these $4^{10} =2^{20} >10^6$ $k$ | + | *In case of a quaternary source $(M = 4)$ it must already be averaged over $4^{10} = 1\hspace{0.08cm}048\hspace{0.08cm}576$ summation terms for the determination of $H_{10}$. |
| + | |||
| + | * Considering that each of these $4^{10} =2^{20} >10^6$ $k$–tuple should occur in simulation/time averaging about $100$ times (statistical guideline) to ensure sufficient simulation accuracy, it follows that the sequence length should be in this case greater than $N = 10^8$. | ||
| Line 160: | Line 172: | ||
In this special case, the $H_k$ approximation must be determined independently from $k$ by averaging only two compound probabilities: | In this special case, the $H_k$ approximation must be determined independently from $k$ by averaging only two compound probabilities: | ||
* $k = 2$: $p_{\rm AB} = p_{\rm BA} = 1/2$ ⇒ $H_2 = 1/2 \hspace{0.2cm} \rm bit/symbol$, | * $k = 2$: $p_{\rm AB} = p_{\rm BA} = 1/2$ ⇒ $H_2 = 1/2 \hspace{0.2cm} \rm bit/symbol$, | ||
| + | |||
* $k = 3$: $p_{\rm ABA} = p_{\rm BAB} = 1/2$ ⇒ $H_3 = 1/3 \hspace{0.2cm} \rm bit/symbol$, | * $k = 3$: $p_{\rm ABA} = p_{\rm BAB} = 1/2$ ⇒ $H_3 = 1/3 \hspace{0.2cm} \rm bit/symbol$, | ||
| + | |||
* $k = 4$: $p_{\rm ABAB} = p_{\rm BABA} = 1/2$ ⇒ $H_4 = 1/4 \hspace{0.2cm} \rm bit/symbol$. | * $k = 4$: $p_{\rm ABAB} = p_{\rm BABA} = 1/2$ ⇒ $H_4 = 1/4 \hspace{0.2cm} \rm bit/symbol$. | ||
| − | The | + | The entropy of this alternating binary sequence is therefore |
:$$H = \lim_{k \rightarrow \infty }{1}/{k} = 0 \hspace{0.05cm}.$$ | :$$H = \lim_{k \rightarrow \infty }{1}/{k} = 0 \hspace{0.05cm}.$$ | ||
| − | The result was to be expected, since the considered sequence has only minimal information, which does not affect the entropy end value $H$ namely: <br> "Does $\rm A$ occur at the even or the odd times?" | + | The result was to be expected, since the considered sequence has only minimal information, which does not affect the entropy end value $H$, namely: <br> "Does $\rm A$ occur at the even or the odd times?" |
You can see that $H_k$ comes closer to this final value $H = 0$ very slowly: The twentieth entropy approximation still returns $H_{20} = 0.05 \hspace{0.05cm} \rm bit/symbol$. }} | You can see that $H_k$ comes closer to this final value $H = 0$ very slowly: The twentieth entropy approximation still returns $H_{20} = 0.05 \hspace{0.05cm} \rm bit/symbol$. }} | ||
| Line 174: | Line 188: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Summary of the results of the last | + | $\text{Summary of the results of the last sections:}$ |
| − | *Generally it applies to the ''' | + | *Generally it applies to the »'''entropy of a message source'''«: |
:$$H \le \text{...} \le H_3 \le H_2 \le H_1 \le H_0 | :$$H \le \text{...} \le H_3 \le H_2 \le H_1 \le H_0 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *A '''redundancy-free source'' exists if all $M$ symbols are equally probable and there are no statistical | + | *A »'''redundancy-free source'''« exists if all $M$ symbols are equally probable and there are no statistical bindings within the sequence. <br> For these hold $(r$ denotes the ''relative redundancy'' $)$: |
:$$H = H_0 = H_1 = H_2 = H_3 = \text{...}\hspace{0.5cm} | :$$H = H_0 = H_1 = H_2 = H_3 = \text{...}\hspace{0.5cm} | ||
\Rightarrow \hspace{0.5cm} r = \frac{H - H_0}{H_0}= 0 \hspace{0.05cm}.$$ | \Rightarrow \hspace{0.5cm} r = \frac{H - H_0}{H_0}= 0 \hspace{0.05cm}.$$ | ||
| − | *A '''memoryless source''' can be quite redundant $(r> 0)$. This redundancy then is solely due to the deviation of the symbol probabilities from the uniform distribution. Here the following relations are valid | + | *A »'''memoryless source'''« can be quite redundant $(r> 0)$. This redundancy then is solely due to the deviation of the symbol probabilities from the uniform distribution. Here the following relations are valid: |
:$$H = H_1 = H_2 = H_3 = \text{...} \le H_0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm}0 \le r = \frac{H_1 - H_0}{H_0}< 1 \hspace{0.05cm}.$$ | :$$H = H_1 = H_2 = H_3 = \text{...} \le H_0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm}0 \le r = \frac{H_1 - H_0}{H_0}< 1 \hspace{0.05cm}.$$ | ||
| − | *The corresponding condition for a '''source with memory''' is | + | *The corresponding condition for a »'''source with memory'''« is |
:$$ H <\text{...} < H_3 < H_2 < H_1 \le H_0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} 0 < r = \frac{H_1 - H_0}{H_0}\le1 \hspace{0.05cm}.$$ | :$$ H <\text{...} < H_3 < H_2 < H_1 \le H_0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} 0 < r = \frac{H_1 - H_0}{H_0}\le1 \hspace{0.05cm}.$$ | ||
*If $H_2 < H_1$, then $H_3 < H_2$, $H_4 < H_3$, etc. ⇒ In the general equation, the "≤" character must be replaced by the "<" character. | *If $H_2 < H_1$, then $H_3 < H_2$, $H_4 < H_3$, etc. ⇒ In the general equation, the "≤" character must be replaced by the "<" character. | ||
| − | *If the symbols are equally probable, then again $H_1 = H_0$, while $H_1 < H_0$ applies to symbols which are not equally probable.}} | + | |
| + | *If the symbols are equally probable, then again $H_1 = H_0$, while $H_1 < H_0$ applies to symbols which are not equally probable.}} | ||
| − | ==The | + | ==The entropy of the AMI code == |
<br> | <br> | ||
| − | In chapter [[Digital_Signal_Transmission/ | + | In chapter [[Digital_Signal_Transmission/Symbolwise_Coding_with_Pseudo-Ternary_Codes#Properties_of_the_AMI_code|"Symbol-wise Coding with Pseudo-Ternary Codes"]] of the book "Digital Signal Transmission", among other things, the AMI pseudo-ternary code is discussed. |
| + | [[File:EN_Inf_T_1_2_S4.png|right|frame|Signals and symbol sequences for AMI code]] | ||
| + | |||
*This converts the binary sequence $〈 q_ν 〉$ with $q_ν ∈ \{ \rm L, \ H \}$ into the ternary sequence $〈 c_ν 〉$ with $q_ν ∈ \{ \rm M, \ N, \ P \}$. | *This converts the binary sequence $〈 q_ν 〉$ with $q_ν ∈ \{ \rm L, \ H \}$ into the ternary sequence $〈 c_ν 〉$ with $q_ν ∈ \{ \rm M, \ N, \ P \}$. | ||
| − | *The names of the source symbols stand for $\rm L$ow and $\rm H$igh and those of the code symbols for $\rm M$inus, $\rm | + | |
| + | *The names of the source symbols stand for $\rm L$(ow) and $\rm H$(igh) and those of the code symbols for $\rm M$(inus), $\rm P$(lus), and $\rm N$(ull) ⇒ "Zero". | ||
| − | The coding rule of the AMI code ("Alternate Mark Inversion") is | + | The coding rule of the AMI code ("Alternate Mark Inversion") is: |
| − | |||
*Each binary symbol $q_ν =\rm L$ is represented by the code symbol $c_ν =\rm N$ . | *Each binary symbol $q_ν =\rm L$ is represented by the code symbol $c_ν =\rm N$ . | ||
| − | |||
| + | *In contrast, $q_ν =\rm H$ alternates with $c_ν =\rm P$ and $c_ν =\rm M$ coded ⇒ name "Alternate Mark Inversion". | ||
| − | This special encoding adds redundancy with the sole purpose of ensuring that the | + | *This special encoding adds redundancy with the sole purpose of ensuring that the encoded sequence does not contain a DC component. |
<br clear=all> | <br clear=all> | ||
However, we do not consider the spectral properties of the AMI code here, but interpret this code information-theoretically: | However, we do not consider the spectral properties of the AMI code here, but interpret this code information-theoretically: | ||
| − | *Based on the | + | *Based on the symbol set size $M = 3$ the decision content of the (ternary) encoded sequence is equal to $H_0 = \log_2 \ 3 ≈ 1.585 \hspace{0.05cm} \rm bit/symbol$. The first entropy approximation returns $H_1 = 1.5 \hspace{0.05cm} \rm bit/symbol$, as shown in the following calculation: |
:$$p_{\rm H} = p_{\rm L} = 1/2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | :$$p_{\rm H} = p_{\rm L} = 1/2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| Line 214: | Line 231: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *Let's now look at two-tuples. With AMI code, $\rm P$ cannot follow $\rm P$ and $\rm M$ cannot follow $\rm M$ | + | *Let's now look at two-tuples. With the AMI code, $\rm P$ cannot follow $\rm P$ and $\rm M$ cannot follow $\rm M$. The probability for $\rm NN$ is equal to $p_{\rm L} \cdot p_{\rm L} = 1/4$. All other (six) two-tuples occur with the probability $1/8$. From this follows for the second entropy approximation: |
:$$H_2 = 1/2 \cdot \big [ 1/4 \cdot {\rm log_2}\hspace{0.1cm}4 + 6 \cdot 1/8 \cdot {\rm log_2}\hspace{0.1cm}8 \big ] = 1,375 \,{\rm bit/symbol} \hspace{0.05cm}.$$ | :$$H_2 = 1/2 \cdot \big [ 1/4 \cdot {\rm log_2}\hspace{0.1cm}4 + 6 \cdot 1/8 \cdot {\rm log_2}\hspace{0.1cm}8 \big ] = 1,375 \,{\rm bit/symbol} \hspace{0.05cm}.$$ | ||
| Line 220: | Line 237: | ||
:$$ H < \hspace{0.05cm}\text{...}\hspace{0.05cm} < H_5 < H_4 < H_3 < H_2 = 1.375 \,{\rm bit/symbol} \hspace{0.05cm}.$$ | :$$ H < \hspace{0.05cm}\text{...}\hspace{0.05cm} < H_5 < H_4 < H_3 < H_2 = 1.375 \,{\rm bit/symbol} \hspace{0.05cm}.$$ | ||
| − | *Exceptionally in this example we know the actual entropy $H$ of the | + | *Exceptionally in this example we know the actual entropy $H$ of the encoded sequence $〈 c_ν 〉$: Since no new information is added by the coder and no information is lost, it is the same entropy $H = 1 \,{\rm bit/symbol} $ as the one of the redundancy-free binary sequence $〈 q_ν 〉$. |
| − | The [[Aufgaben: | + | The [[Aufgaben:Exercise_1.4:_Entropy_Approximations_for_the_AMI_Code|"Exercise 1.4"]] shows the considerable effort required to calculate the entropy approximation $H_3$. Moreover, $H_3$ still deviates significantly from the final value $H = 1 \,{\rm bit/symbol} $. A faster result is achieved if the AMI code is described by a Markov chain as explained in the next section. |
| Line 230: | Line 247: | ||
[[File:Inf_T_1_2_S5_vers2.png|right|frame|Markov processes with $M = 2$ states]] | [[File:Inf_T_1_2_S5_vers2.png|right|frame|Markov processes with $M = 2$ states]] | ||
| − | Sequences with statistical | + | Sequences with statistical bindings between the sequence elements (symbols) are often modeled by [[Theory_of_Stochastic_Signals/Markov_Chains|$\text{Markov processes}$]] where we limit ourselves here to first-order Markov processes. First we consider a binary Markov process $(M = 2)$ with the states (symbols) $\rm A$ and $\rm B$. |
On the right, you can see the transition diagram for a first-order binary Markov process however, only two of the four transfer probabilities given are freely selectable, for example | On the right, you can see the transition diagram for a first-order binary Markov process however, only two of the four transfer probabilities given are freely selectable, for example | ||
* $p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}} = \rm Pr(A\hspace{0.01cm}|\hspace{0.01cm}B)$ ⇒ conditional probability that $\rm A$ follows $\rm B$ . | * $p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}} = \rm Pr(A\hspace{0.01cm}|\hspace{0.01cm}B)$ ⇒ conditional probability that $\rm A$ follows $\rm B$ . | ||
| + | |||
* $p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}} = \rm Pr(B\hspace{0.01cm}|\hspace{0.01cm}A)$ ⇒ conditional probability that $\rm B$ follows $\rm A$ . | * $p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}} = \rm Pr(B\hspace{0.01cm}|\hspace{0.01cm}A)$ ⇒ conditional probability that $\rm B$ follows $\rm A$ . | ||
| − | For the other two transition probabilities $p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} = 1- p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}$ and $p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} = 1- p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} | + | For the other two transition probabilities: $p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} = 1- p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}$ and $p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} = 1- p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} |
\hspace{0.05cm}.$ | \hspace{0.05cm}.$ | ||
| − | Due to the presupposed properties [[Theory_of_Stochastic_Signals/Auto | + | Due to the presupposed properties [[Theory_of_Stochastic_Signals/Auto-Correlation_Function_(ACF)#Stationary_random_processes|$\text{Stationarity}$]] and [[Theory_of_Stochastic_Signals/Auto-Correlation_Function_(ACF)#Ergodic_random_processes|$\text{Ergodicity}$]] the following applies to the state or symbol probabilities: |
:$$p_{\rm A} = {\rm Pr}({\rm A}) = \frac{p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}}{p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} | :$$p_{\rm A} = {\rm Pr}({\rm A}) = \frac{p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}}{p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} | ||
| Line 246: | Line 264: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | These equations allow first information theoretical statements about the Markov processes: | + | These equations allow first information–theoretical statements about the Markov processes: |
| − | * For $p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}} = p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}}$ the symbols are equally likely ⇒ $p_{\text{A}} = p_{\text{B}}= 0.5$. The first entropy approximation returns $H_1 = H_0 = 1 \hspace{0.05cm} \rm bit/symbol$, independent of the actual values of the (conditional) transition probabilities $p_{\text{A|B}}$ | + | * For $p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}} = p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}}$ the symbols are equally likely ⇒ $p_{\text{A}} = p_{\text{B}}= 0.5$. The first entropy approximation returns $H_1 = H_0 = 1 \hspace{0.05cm} \rm bit/symbol$, independent of the actual values of the (conditional) transition probabilities $p_{\text{A|B}}$ and $p_{\text{B|A}}$. |
| − | * | + | |
| + | *But the source entropy $H$ as the limit value $($for $k \to \infty)$ of the [[Information_Theory/Discrete_Sources_with_Memory#Generalization_to_.7F.27.22.60UNIQ-MathJax111-QINU.60.22.27.7F-tuple_and_boundary_crossing|"Entropy approximation of order $k$"]] ⇒ $H_k$ depends very much on the actual values of $p_{\text{A|B}}$ and $p_{\text{B|A}}$ and not only on their quotients. This is shown by the following example. | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Example 6:}$ | $\text{Example 6:}$ | ||
| − | We consider three binary symmetric Markov sources that are represented by the numerical values of the symmetric transition probabilities $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} }$ | + | We consider three binary symmetric Markov sources that are represented by the numerical values of the symmetric transition probabilities $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} }$. For the symbol probabilities the following applies: $p_{\rm A} = p_{\rm B}= 0.5$, and the other transition probabilities have the values |
| − | [[File:EN_Inf_T_1_2_S5b.png|right|frame|Three examples of binary Markov sources]] | + | [[File:EN_Inf_T_1_2_S5b.png|right|frame|Three examples of binary Markov sources with $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} }$ ]] |
:$$p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 1 - p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = | :$$p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 1 - p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = | ||
p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}B} }.$$ | p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}B} }.$$ | ||
| − | *The middle (blue) | + | *The middle (blue) sequence with $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 0.5$ has the entropy $H ≈ 1 \hspace{0.1cm} \rm bit/symbol$. That means: In this special case there are no statistical bindings within the sequence. |
| − | *The left (red) sequence with $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 0.2$ has less changes between $\rm A$ and $\rm B$ | + | *The left (red) sequence with $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 0.2$ has less changes between $\rm A$ and $\rm B$. Due to statistical dependencies between neighboring symbols the entropy is now smaller: $H ≈ 0.72 \hspace{0.1cm} \rm bit/symbol$. |
| − | *The right (green) symbol sequence with $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 0.8$ has the exact same entropy $H ≈ 0.72 \hspace{0.1cm} \rm bit/symbol$ as the red sequence. Here you can see many | + | *The right (green) symbol sequence with $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 0.8$ has the exact same entropy $H ≈ 0.72 \hspace{0.1cm} \rm bit/symbol$ as the red sequence. Here you can see many regions with alternating symbols $($... $\rm ABABAB$ ... $)$.}} |
This example is worth noting: | This example is worth noting: | ||
| − | + | #If you had not used the Markov properties of the red and green sequences, you would have reached the respective result $H ≈ 0.72 \hspace{0.1cm} \rm bit/symbol$ only after lengthy calculations. | |
| − | + | #The following sections show that for a source with Markov properties the final value $H$ can be determined from the entropy approximations $H_1$ and $H_2$ alone. Likewise, all entropy approximations $H_1$ and $H_2$ can also be calculated from $H_k$ for $k$–tuples in a simple manner ⇒ $H_3$, $H_4$, $H_5$, ... $H_{100}$, ... | |
| Line 274: | Line 293: | ||
<br> | <br> | ||
[[File:Inf_T_1_2_S5_vers2.png|right|frame|Markov processes with $M = 2$ states]] | [[File:Inf_T_1_2_S5_vers2.png|right|frame|Markov processes with $M = 2$ states]] | ||
| − | We continue to assume the first-order symmetric binary Markov source. As | + | We continue to assume the first-order symmetric binary Markov source. As in the previous section, we use the following nomenclature for |
| − | *the transition probabilities $p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}}$, $p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}}$, $p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}A}}= 1- p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}}$, $p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}B}} = 1 - p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}}$, | + | *the transition probabilities ⇒ $p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}}$, $p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}}$, $p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}A}}= 1- p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}}$, $p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}B}} = 1 - p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}}$, |
| − | *the ergodic probabilities $p_{\text{A}}$ and $p_{\text{B}}$, | + | |
| − | + | *the ergodic probabilities ⇒ $p_{\text{A}}$ and $p_{\text{B}}$, | |
| + | *the compound probabilities, for example ⇒ $p_{\text{AB}} = p_{\text{A}} - p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}}$. | ||
| − | We now compute the [[Information_Theory/ | + | We now compute the [[Information_Theory/Discrete_Sources_with_Memory#Entropy_with_respect_to_two-tuples|"Entropy of a two-tuple"]] (with the unit "bit/two-tuple"): |
:$$H_2\hspace{0.05cm}' = p_{\rm A} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm A} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm B} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} + p_{\rm B} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}} | :$$H_2\hspace{0.05cm}' = p_{\rm A} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm A} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm B} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} + p_{\rm B} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}} | ||
| Line 293: | Line 313: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Conclusion:}$ Thus the '''second entropy approximation''' (with the unit "bit/symbol"): | + | $\text{Conclusion:}$ Thus the »'''second entropy approximation'''« (with the unit "bit/symbol") is: |
:$$H_2 = {1}/{2} \cdot {H_2\hspace{0.05cm}'} = {1}/{2} \cdot \big [ H_{\rm 1} + H_{\rm M} \big] | :$$H_2 = {1}/{2} \cdot {H_2\hspace{0.05cm}'} = {1}/{2} \cdot \big [ H_{\rm 1} + H_{\rm M} \big] | ||
\hspace{0.05cm}.$$}} | \hspace{0.05cm}.$$}} | ||
| − | is to be noted: | + | It is to be noted: |
| − | + | #The first summand $H_1$ ⇒ first entropy approximation depends only on the symbol probabilities. | |
| − | + | #For a symmetrical Markov process ⇒ $p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}} = p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}} $ ⇒ $p_{\text{A}} = p_{\text{B}} = 1/2$ the result for this first summand is $H_1 = 1 \hspace{0.1cm} \rm bit/symbol$. | |
| − | + | #The second summand $H_{\text{M}}$ must be calculated according to the second of the two upper equations. | |
| − | + | #For a symmetrical Markov process you get $H_{\text{M}} = H_{\text{bin}}(p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}})$. | |
| − | Now, this result is extended to the $k$ | + | Now, this result is extended to the $k$–th entropy approximation. Here, the advantage of Markov sources over other sources is taken advantage of, that the entropy calculation for $k$–tuples is very simple. For each Markov source, the following applies |
:$$H_k = {1}/{k} \cdot \big [ H_{\rm 1} + (k-1) \cdot H_{\rm M}\big ] \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | :$$H_k = {1}/{k} \cdot \big [ H_{\rm 1} + (k-1) \cdot H_{\rm M}\big ] \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | ||
| Line 326: | Line 346: | ||
| − | However, these approximations are not very important. Mostly only the limit value $H$. For sources without | + | However, these approximations are not very important. Mostly only the limit value $H$ is of interest. For sources without Markov properties the approximations $H_k$ are calculated only to be able to estimate this limit value, i.e. the actual entropy. |
| + | |||
| + | <u>Notes</u>: | ||
| + | *In the [[Aufgaben:Exercise_1.5:_Binary_Markov_Source|"Exercise 1.5"]] the above equations are applied to the more general case of an asymmetric binary source. | ||
| − | + | *All equations in this section also apply to non-binary Markov sources $(M > 2)$ as shown in the next section. | |
| − | |||
| − | *All equations | ||
| Line 337: | Line 358: | ||
==Non-binary Markov sources == | ==Non-binary Markov sources == | ||
<br> | <br> | ||
| − | [[File:EN_Inf_T_1_2_S6.png|right|frame|Ternary and | + | [[File:EN_Inf_T_1_2_S6.png|right|frame|Ternary and quaternary first order Markov source]] |
| − | The following equations apply to each Markov source regardless of the symbol | + | The following equations apply to each Markov source regardless of the symbol set size $M$: |
:$$H = 2 \cdot H_2 - H_{\rm 1} \hspace{0.05cm},$$ | :$$H = 2 \cdot H_2 - H_{\rm 1} \hspace{0.05cm},$$ | ||
| Line 348: | Line 369: | ||
These equations allow the simple calculation of the entropy $H$ from the approximations $H_1$ and $H_2$. | These equations allow the simple calculation of the entropy $H$ from the approximations $H_1$ and $H_2$. | ||
| − | We now look at the transition diagrams sketched on the right | + | We now look at the transition diagrams sketched on the right: |
| − | * | + | *A ternary Markov source $\rm MQ3$ $(M = 3$, blue coloring$)$, and |
| + | |||
*a quaternary Markov source $\rm MQ4$ $(M = 4$, red color$)$. | *a quaternary Markov source $\rm MQ4$ $(M = 4$, red color$)$. | ||
<br clear=all> | <br clear=all> | ||
| − | In [[Aufgaben: | + | In [[Aufgaben:Exercise_1.6:_Non-Binary_Markov_Sources|"Exercise 1.6"]] the entropy approximations $H_k$ and the total entropy $H$ are calculated as the limit of $H_k$ for $k \to \infty$ . The results are shown in the following figure. All entropies specified there have the unit "bit/symbol". |
| − | [[File:EN_Inf_T_1_2_S6b.png| | + | [[File:EN_Inf_T_1_2_S6b.png|right|frame|Entropies for $\rm MQ3$, $\rm MQ4$ and the $\rm AMI$ code]] |
These results can be interpreted as follows: | These results can be interpreted as follows: | ||
| − | *For the ternary markov source $\rm MQ3$ the entropy approximations of $H_1 = 1 | + | *For the ternary markov source $\rm MQ3$ the entropy approximations of $H_1 = 1.500$ above $H_2 = 1.375$ up to the limit $H = 1.250$ continuously decreasing. Because of $M = 3$ ⇒ $H_0 = 1.585$. |
| − | *For the quaternary Markov source $\rm MQ4$ one receives $H_0 = H_1 = 2 | + | |
| − | *The two models $\rm MQ3$ and $\rm MQ4$ were created during the attempt to calculate the [[Information_Theory/ | + | *For the quaternary Markov source $\rm MQ4$ one receives $H_0 = H_1 = 2.000$ (since four equally probable states) and $H_2 = 1.5$. From the $H_1$- and $H_2$-values all entropy approximations $H_k$ and the final value $H = 1.000$ can be calculated. |
| − | *The entropy approximations $H_1$, $H_2$ and $H_3$ of the AMI code (green markers) were calculated in the [[Aufgaben:Aufgabe 1.4: Entropienäherungen für den AMI-Code|Exercise 1.4]] | + | |
| − | *You can see that the Markov model $\rm MQ3$ for $H_0 = 1 | + | *The two models $\rm MQ3$ and $\rm MQ4$ were created during the attempt to calculate the [[Information_Theory/Discrete_Sources_with_Memory#The_entropy_of_the_AMI_code|"AMI code"]] to be described information–theoretically by Markov sources. The symbols $\rm M$, $\rm N$ and $\rm P$ stand for "minus", "zero" and "plus". |
| + | |||
| + | *The entropy approximations $H_1$, $H_2$ and $H_3$ of the AMI code (green markers) were calculated in the [[Aufgaben:Aufgabe 1.4: Entropienäherungen für den AMI-Code|"Exercise 1.4"]]. On the calculation of $H_4$, $H_5$, ... had to be omitted for reasons of effort. But the final value of $H_k$ for $k \to \infty$ ⇒ $H = 1.000$ is known. | ||
| + | |||
| + | *You can see that the Markov model $\rm MQ3$ for $H_0 = 1.585$, $H_1 = 1.500$ and $H_2 = 1.375$ yields exactly the same numerical values as the AMI code. On the other hand $H_3$ ⇒ $(1.333$ instead of $1.292)$ and especially the final value $H$ ⇒ $(1.250$ compared to $1.000)$. | ||
| + | |||
*The model $\rm MQ4$ $(M = 4)$ differs from the AMI code $(M = 3)$ with respect to the decision content $H_0$ and also with respect to all entropy approximations $H_k$. Nevertheless, $\rm MQ4$ is the more suitable model for the AMI code, since the final value $H = 1,000$ is the same. | *The model $\rm MQ4$ $(M = 4)$ differs from the AMI code $(M = 3)$ with respect to the decision content $H_0$ and also with respect to all entropy approximations $H_k$. Nevertheless, $\rm MQ4$ is the more suitable model for the AMI code, since the final value $H = 1,000$ is the same. | ||
| + | |||
*The model $\rm MQ3$ yields entropy values that are too large, since the sequences $\rm PNP$ and $\rm MNM$ are possible here, which cannot occur in the AMI code. Already with the approximation $H_3$ the difference is slightly noticeable, in the final value $H$ even clearly $(1.25$ instead of $1)$. | *The model $\rm MQ3$ yields entropy values that are too large, since the sequences $\rm PNP$ and $\rm MNM$ are possible here, which cannot occur in the AMI code. Already with the approximation $H_3$ the difference is slightly noticeable, in the final value $H$ even clearly $(1.25$ instead of $1)$. | ||
| − | In the model $\rm MQ4$ the state " | + | In the model $\rm MQ4$ the state "Zero" was split into two states $\rm N$ and $\rm O$ (see upper right figure in this section): |
| − | *Here applies to the state $\rm N$: The current binary symbol $\rm L$ is | + | *Here applies to the state $\rm N$: The current binary symbol $\rm L$ is encoded with the amplitude value $0$ (zero), as per the AMI rule. The next occurring $\rm H$ symbol, on the other hand, is displayed as $-1$ (minus), because the last symol $\rm H$ was encoded as $+1$ (plus). |
| − | * | + | |
| + | *Also with the state $\rm O$ the current binary symbol $\rm L$ is represented with the ternary value $0$. In contrast to the state $\rm N$ however, the next occurring $\rm H$ symbol is now encoded as $+1$ (plus) since the last $\rm H$ symbol was encoded as $-1$ (minus). | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Conclusion:}$ | $\text{Conclusion:}$ | ||
| − | + | #The $\rm MQ4$ output sequence actually follows the rules of the AMI code and has entropy $H = 1.000 \hspace{0.15cm} \rm bit/symbol$. | |
| − | + | #But because of the new state $\rm O$ now $H_0 = 2.000 \hspace{0.15cm} \rm bit/symbol$ $($against $1.585 \hspace{0.15cm} \rm bit/symbol)$ is clearly too large. | |
| − | + | #Also all $H_k$ approximations are larger than with the AMI code. First for $k \to \infty$ the model $\rm MQ4$ and the AMI code match exactly: $H = 1.000 \hspace{0.15cm} \rm bit/symbol$.}} | |
| − | |||
== Exercises for the chapter== | == Exercises for the chapter== | ||
<br> | <br> | ||
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_1.3:_Entropy_Approximations|Exercise 1.3: Entropy Approximations]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_1.4:_Entropy_Approximations_for_the_AMI_Code|Exercise 1.4: Entropy Approximations for the AMI Code]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_1.4Z:_Entropy_of_the_AMI_Code|Exercise 1.4Z: Entropy of the AMI Code]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_1.5:_Binary_Markov_Source|Exercise 1.5: Binary Markov Source]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_1.5Z:_Symmetrical_Markov_Source|Exercise 1.5Z: Symmetrical Markov Source]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_1.6:_Non-Binary_Markov_Sources|Exercise 1.6: Non-Binary Markov Sources]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_1.6Z:_Ternary_Markov_Source|Exercise 1.6Z:Ternary Markov Source]] |
{{Display}} | {{Display}} | ||
Latest revision as of 17:19, 14 February 2023
Contents
A simple introductory example
$\text{Example 1:}$ At the "beginning of the first chapter" we have considered a memoryless message source with the symbol set $\rm \{A, \ B, \ C, \ D\}$ ⇒ $M = 4$ . An exemplary symbol sequence is shown again in the following figure as source $\rm Q1$ .
- With the symbol probabilities $p_{\rm A} = 0.4 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.3 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.2 \hspace{0.05cm},\hspace{0.2cm} p_{\rm D} = 0.1\hspace{0.05cm}$ the entropy is
- $$H \hspace{-0.05cm}= 0.4 \cdot {\rm log}_2\hspace{0.05cm}\frac {1}{0.4} + 0.3 \cdot {\rm log}_2\hspace{0.05cm}\frac {1}{0.3} + 0.2 \cdot {\rm log}_2\hspace{0.05cm}\frac {1}{0.2} + 0.1 \cdot {\rm log}_2\hspace{0.05cm}\frac {1}{0.1} \approx 1.84 \hspace{0.05cm}{\rm bit/symbol} \hspace{0.01cm}.$$
- Due to the unequal symbol probabilities the entropy is smaller than $H_0 = \log_2 M = 2 \hspace{0.05cm} \rm bit/symbol$.
The source $\rm Q2$ is almost identical to the source $\rm Q1$, except that each individual symbol is output not only once, but twice in a row: $\rm A ⇒ AA$, $\rm B ⇒ BB$, and so on.
- It is obvious that $\rm Q2$ has a smaller entropy (uncertainty) than $\rm Q1$.
- Because of the simple repetition code, the entropy
- $$H = 1.84/2 = 0.92 \hspace{0.05cm} \rm bit/symbol$$
- has only half the size, although the occurrence probabilities have not changed.
$\text{Conclusion:}$ This example shows:
- The entropy of a source with memory is smaller than the entropy of a memoryless source with equal symbol probabilities.
- The statistical bindings within the sequence $〈 q_ν 〉$ have to be considered now,
- namely the dependency of the symbol $q_ν$ from the predecessor symbols $q_{ν-1}$, $q_{ν-2}$, ...
Entropy with respect to two-tuples
We continue to look at the source symbol sequence $〈 q_1, \hspace{0.05cm} q_2,\hspace{0.05cm}\text{ ...} \hspace{0.05cm}, q_{ν-1}, \hspace{0.05cm}q_ν, \hspace{0.05cm}\hspace{0.05cm}q_{ν+1} .\hspace{0.05cm}\text{...} \hspace{0.05cm}〉$ and now consider the entropy of two successive source symbols.
- All source symbols $q_ν$ are taken from an alphabet with the symbol set size $M$, so that for the combination $(q_ν, \hspace{0.05cm}q_{ν+1})$ there are exactly $M^2$ possible symbol pairs with the following "combined probabilities":
- $${\rm Pr}(q_{\nu}\cap q_{\nu+1})\le {\rm Pr}(q_{\nu}) \cdot {\rm Pr}( q_{\nu+1}) \hspace{0.05cm}.$$
- From this, the »compound entropy« of two consecutive symbols can be computed:
- $$H_2\hspace{0.05cm}' = \sum_{q_{\nu}\hspace{0.05cm} \in \hspace{0.05cm}\{ \hspace{0.05cm}q_{\mu}\hspace{0.01cm} \}} \ \sum_{q_{\nu+1}\hspace{0.05cm} \in \hspace{0.05cm}\{ \hspace{0.05cm} q_{\mu}\hspace{0.01cm} \}}\hspace{-0.1cm}{\rm Pr}(q_{\nu}\cap q_{\nu+1}) \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{{\rm Pr}(q_{\nu}\cap q_{\nu+1})} \hspace{0.4cm}({\rm unit\hspace{-0.1cm}: \hspace{0.1cm}bit/two–tuple}) \hspace{0.05cm}.$$
- The index "2" symbolizes that the entropy thus calculated refers to »two-tuples«.
- To get the average information content per symbol, $H_2\hspace{0.05cm}'$ has to be divided in half:
- $$H_2 = {H_2\hspace{0.05cm}'}/{2} \hspace{0.5cm}({\rm unit\hspace{-0.1cm}: \hspace{0.1cm}bit/symbol}) \hspace{0.05cm}.$$
- In order to achieve a consistent nomenclature, we now label the entropy defined in chapter "Memoryless Message Sources" with $H_1$:
- $$H_1 = \sum_{q_{\nu}\hspace{0.05cm} \in \hspace{0.05cm}\{ \hspace{0.05cm}q_{\mu}\hspace{0.01cm} \}} {\rm Pr}(q_{\nu}) \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{{\rm Pr}(q_{\nu})} \hspace{0.5cm}({\rm unit\hspace{-0.1cm}: \hspace{0.1cm}bit/symbol}) \hspace{0.05cm}.$$
- The index "1" is supposed to indicate that $H_1$ considers only the symbol probabilities and not statistical bindings between symbols within the sequence. With $H_0 = \log_2 \ M$ the following size relation results:
- $$H_0 \ge H_1 \ge H_2 \hspace{0.05cm}.$$
- With statistical independence of the sequence elements ⇒ $H_2 = H_1$.
The previous equations each indicate an "ensemble mean value". The probabilities required for the calculation of $H_1$ and $H_2$ can, however, also be calculated as time averages from a very long sequence or, more precisely, approximated by the corresponding "relative frequencies".
Let us now illustrate the calculation of entropy approximations $H_1$ and $H_2$ with three examples.
$\text{Example 2:}$ We will first look at the sequence $〈 q_1$, ... , $q_{50} \rangle $ according to the graphic, where the sequence elements $q_ν$ originate from the alphabet $\rm \{A, \ B, \ C \}$ ⇒ the symbol set size is $M = 3$.
- By time averaging over $50$ symbols one gets the symbol probabilities $p_{\rm A} ≈ 0.5$, $p_{\rm B} ≈ 0.3$ and $p_{\rm C} ≈ 0.2$, with which one can calculate the first order entropy approximation:
- $$H_1 = 0.5 \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{0.5} + 0.3 \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{0.3} + 0.2 \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{0.2} \approx \, 1.486 \,{\rm bit/symbol} \hspace{0.05cm}.$$
- Due to the not equally probable symbols $H_1 < H_0 = 1.585 \hspace{0.05cm}. \rm bit/symbol$. As an approximation for the probabilities of two-tuples one gets from the above sequence:
- $$\begin{align*}p_{\rm AA} \hspace{-0.1cm}& = \hspace{-0.1cm} 14/49\hspace{0.05cm}, \hspace{0.2cm}p_{\rm AB} = 8/49\hspace{0.05cm}, \hspace{0.2cm}p_{\rm AC} = 3/49\hspace{0.05cm}, \\\ p_{\rm BA} \hspace{-0.1cm}& = \hspace{0.07cm} 7/49\hspace{0.05cm}, \hspace{0.25cm}p_{\rm BB} = 2/49\hspace{0.05cm}, \hspace{0.2cm}p_{\rm BC} = 5/49\hspace{0.05cm}, \\\ p_{\rm CA} \hspace{-0.1cm}& = \hspace{0.07cm} 4/49\hspace{0.05cm}, \hspace{0.25cm}p_{\rm CB} = 5/49\hspace{0.05cm}, \hspace{0.2cm}p_{\rm CC} = 1/49\hspace{0.05cm}.\end{align*}$$
- Please note that the $50$ sequence elements can only be formed from $49$ two-tuples $(\rm AA$, ... , $\rm CC)$ which are marked in different colors in the graphic.
- The entropy approximation $H_2$ should actually be equal to $H_1$ since the given symbol sequence comes from a memoryless source.
- Because of the short sequence length $N = 50$ and the resulting statistical inaccuracy, however, a smaller value results:
- $$H_2 ≈ 1.39\hspace{0.05cm} \rm bit/symbol.$$
$\text{Example 3:}$ Now let us consider a »memoryless binary source« with equally probable symbols, i.e. there would be $p_{\rm A} = p_{\rm B} = 1/2$. The first twenty subsequent elements are $〈 q_ν 〉 =\rm BBAAABAABBBBBAAAABABAB$ ...
- Because of the equally probable binary symbols $H_1 = H_0 = 1 \hspace{0.05cm} \rm bit/symbol$.
- The compound probability $p_{\rm AB}$ of the combination $\rm AB$ is equal to $p_{\rm A} \cdot p_{\rm B} = 1/4$. Also $p_{\rm AA} = p_{\rm BB} = p_{\rm BA} = 1/4$.
- This gives for the second entropy approximation
- $$H_2 = {1}/{2} \cdot \big [ {1}/{4} \cdot {\rm log}_2\hspace{0.1cm}4 + {1}/{4} \cdot {\rm log}_2\hspace{0.1cm}4 +{1}/{4} \cdot {\rm log}_2\hspace{0.1cm}4 +{1}/{4} \cdot {\rm log}_2\hspace{0.1cm}4 \big ] = 1 \,{\rm bit/symbol} = H_1 = H_0 \hspace{0.05cm}.$$
Note: Due to the short length of the given sequence the probabilities are slightly different: $p_{\rm AA} = 6/19$, $p_{\rm BB} = 5/19$, $p_{\rm AB} = p_{\rm BA} = 4/19$.
$\text{Example 4:}$ The third sequence considered here results from the binary sequence of $\text{Example 3}$ by using a simple repeat code:
- $$〈 q_ν 〉 =\rm BbBbAaAaAaBbAaAaBbBb \text{...} $$
- The repeated symbols are marked by corresponding lower case letters. But it still applies $M=2$.
- Because of the equally probable binary symbols, this also results in $H_1 = H_0 = 1 \hspace{0.05cm} \rm bit/symbol$.
- As shown in "Exercise 1.3" for the compound probabilities we obtain $p_{\rm AA}=p_{\rm BB} = 3/8$ and $p_{\rm AB}=p_{\rm BA} = 1/8$. Hence
- $$\begin{align*}H_2 ={1}/{2} \cdot \big [ 2 \cdot {3}/{8} \cdot {\rm log}_2\hspace{0.1cm} {8}/{3} + 2 \cdot {1}/{8} \cdot {\rm log}_2\hspace{0.1cm}8\big ] = {3}/{8} \cdot {\rm log}_2\hspace{0.1cm}8 - {3}/{8} \cdot{\rm log}_2\hspace{0.1cm}3 + {1}/{8} \cdot {\rm log}_2\hspace{0.1cm}8 \approx 0.906 \,{\rm bit/symbol} < H_1 = H_0 \hspace{0.05cm}.\end{align*}$$
A closer look at the task at hand leads to the following conclusion:
- The entropy should actually be $H = 0.5 \hspace{0.05cm} \rm bit/symbol$ (every second symbol does not provide new information).
- The second entropy approximation $H_2 = 0.906 \hspace{0.05cm} \rm bit/symbol$ is much larger than the entropy $H$.
- For the entropy determination, the second order approximation is not sufficient. Rather, one must consider larger contiguous blocks of $k > 2$ symbols.
- In the following, such a block is referred to as "$k$–tuple".
Generalization to $k$-tuple and boundary crossing
For abbreviation we write using the compound probability $p_i^{(k)}$ for a $k$–tuple in general:
- $$H_k = \frac{1}{k} \cdot \sum_{i=1}^{M^k} p_i^{(k)} \cdot {\rm log}_2\hspace{0.1cm} \frac{1}{p_i^{(k)}} \hspace{0.5cm}({\rm unit\hspace{-0.1cm}: \hspace{0.1cm}bit/symbol}) \hspace{0.05cm}.$$
- The control variable $i$ stands for one of the $M^k$ tuples.
- The previously calculated approximation $H_2$ results with $k = 2$.
$\text{Definition:}$ The »entropy of a discrete source with memory« has the following limit:
- $$H = \lim_{k \rightarrow \infty }H_k \hspace{0.05cm}.$$
- For the »entropy approximations« $H_k$ the following relations apply $(H_0=\log_2 M)$:
- $$H \le \text{...} \le H_k \le \text{...} \le H_2 \le H_1 \le H_0 \hspace{0.05cm}.$$
The computational effort will increase with increasing $k$ except for a few special cases (see the following example) and depends on the symbol set size $M$ of course:
- For the calculation of $H_{10}$ for a binary source $(M = 2)$ one must average over $2^{10} = 1024$ terms.
- With each further increase of $k$ by $1$ the number of sum terms doubles.
- In case of a quaternary source $(M = 4)$ it must already be averaged over $4^{10} = 1\hspace{0.08cm}048\hspace{0.08cm}576$ summation terms for the determination of $H_{10}$.
- Considering that each of these $4^{10} =2^{20} >10^6$ $k$–tuple should occur in simulation/time averaging about $100$ times (statistical guideline) to ensure sufficient simulation accuracy, it follows that the sequence length should be in this case greater than $N = 10^8$.
$\text{Example 5:}$ We consider an alternating binary sequence ⇒ $〈 q_ν 〉 =\rm ABABABAB$ ... . Accordingly it holds that $H_0 = H_1 = 1 \hspace{0.1cm} \rm bit/symbol$.
In this special case, the $H_k$ approximation must be determined independently from $k$ by averaging only two compound probabilities:
- $k = 2$: $p_{\rm AB} = p_{\rm BA} = 1/2$ ⇒ $H_2 = 1/2 \hspace{0.2cm} \rm bit/symbol$,
- $k = 3$: $p_{\rm ABA} = p_{\rm BAB} = 1/2$ ⇒ $H_3 = 1/3 \hspace{0.2cm} \rm bit/symbol$,
- $k = 4$: $p_{\rm ABAB} = p_{\rm BABA} = 1/2$ ⇒ $H_4 = 1/4 \hspace{0.2cm} \rm bit/symbol$.
The entropy of this alternating binary sequence is therefore
- $$H = \lim_{k \rightarrow \infty }{1}/{k} = 0 \hspace{0.05cm}.$$
The result was to be expected, since the considered sequence has only minimal information, which does not affect the entropy end value $H$, namely:
"Does $\rm A$ occur at the even or the odd times?"
You can see that $H_k$ comes closer to this final value $H = 0$ very slowly: The twentieth entropy approximation still returns $H_{20} = 0.05 \hspace{0.05cm} \rm bit/symbol$.
$\text{Summary of the results of the last sections:}$
- Generally it applies to the »entropy of a message source«:
- $$H \le \text{...} \le H_3 \le H_2 \le H_1 \le H_0 \hspace{0.05cm}.$$
- A »redundancy-free source« exists if all $M$ symbols are equally probable and there are no statistical bindings within the sequence.
For these hold $(r$ denotes the relative redundancy $)$:
- $$H = H_0 = H_1 = H_2 = H_3 = \text{...}\hspace{0.5cm} \Rightarrow \hspace{0.5cm} r = \frac{H - H_0}{H_0}= 0 \hspace{0.05cm}.$$
- A »memoryless source« can be quite redundant $(r> 0)$. This redundancy then is solely due to the deviation of the symbol probabilities from the uniform distribution. Here the following relations are valid:
- $$H = H_1 = H_2 = H_3 = \text{...} \le H_0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm}0 \le r = \frac{H_1 - H_0}{H_0}< 1 \hspace{0.05cm}.$$
- The corresponding condition for a »source with memory« is
- $$ H <\text{...} < H_3 < H_2 < H_1 \le H_0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} 0 < r = \frac{H_1 - H_0}{H_0}\le1 \hspace{0.05cm}.$$
- If $H_2 < H_1$, then $H_3 < H_2$, $H_4 < H_3$, etc. ⇒ In the general equation, the "≤" character must be replaced by the "<" character.
- If the symbols are equally probable, then again $H_1 = H_0$, while $H_1 < H_0$ applies to symbols which are not equally probable.
The entropy of the AMI code
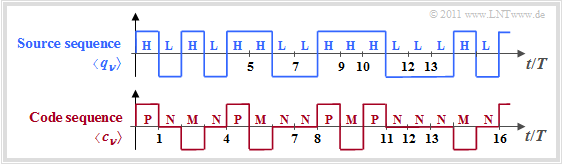
In chapter "Symbol-wise Coding with Pseudo-Ternary Codes" of the book "Digital Signal Transmission", among other things, the AMI pseudo-ternary code is discussed.
- This converts the binary sequence $〈 q_ν 〉$ with $q_ν ∈ \{ \rm L, \ H \}$ into the ternary sequence $〈 c_ν 〉$ with $q_ν ∈ \{ \rm M, \ N, \ P \}$.
- The names of the source symbols stand for $\rm L$(ow) and $\rm H$(igh) and those of the code symbols for $\rm M$(inus), $\rm P$(lus), and $\rm N$(ull) ⇒ "Zero".
The coding rule of the AMI code ("Alternate Mark Inversion") is:
- Each binary symbol $q_ν =\rm L$ is represented by the code symbol $c_ν =\rm N$ .
- In contrast, $q_ν =\rm H$ alternates with $c_ν =\rm P$ and $c_ν =\rm M$ coded ⇒ name "Alternate Mark Inversion".
- This special encoding adds redundancy with the sole purpose of ensuring that the encoded sequence does not contain a DC component.
However, we do not consider the spectral properties of the AMI code here, but interpret this code information-theoretically:
- Based on the symbol set size $M = 3$ the decision content of the (ternary) encoded sequence is equal to $H_0 = \log_2 \ 3 ≈ 1.585 \hspace{0.05cm} \rm bit/symbol$. The first entropy approximation returns $H_1 = 1.5 \hspace{0.05cm} \rm bit/symbol$, as shown in the following calculation:
- $$p_{\rm H} = p_{\rm L} = 1/2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm N} = p_{\rm L} = 1/2\hspace{0.05cm},\hspace{0.2cm}p_{\rm M} = p_{\rm P}= p_{\rm H}/2 = 1/4\hspace{0.3cm} \Rightarrow \hspace{0.3cm} H_1 = 1/2 \cdot {\rm log}_2\hspace{0.1cm}2 + 2 \cdot 1/4 \cdot{\rm log}_2\hspace{0.1cm}4 = 1.5 \,{\rm bit/symbol} \hspace{0.05cm}.$$
- Let's now look at two-tuples. With the AMI code, $\rm P$ cannot follow $\rm P$ and $\rm M$ cannot follow $\rm M$. The probability for $\rm NN$ is equal to $p_{\rm L} \cdot p_{\rm L} = 1/4$. All other (six) two-tuples occur with the probability $1/8$. From this follows for the second entropy approximation:
- $$H_2 = 1/2 \cdot \big [ 1/4 \cdot {\rm log_2}\hspace{0.1cm}4 + 6 \cdot 1/8 \cdot {\rm log_2}\hspace{0.1cm}8 \big ] = 1,375 \,{\rm bit/symbol} \hspace{0.05cm}.$$
- For the further entropy approximations $H_3$, $H_4$, ... and the actual entropy $H$ will apply:
- $$ H < \hspace{0.05cm}\text{...}\hspace{0.05cm} < H_5 < H_4 < H_3 < H_2 = 1.375 \,{\rm bit/symbol} \hspace{0.05cm}.$$
- Exceptionally in this example we know the actual entropy $H$ of the encoded sequence $〈 c_ν 〉$: Since no new information is added by the coder and no information is lost, it is the same entropy $H = 1 \,{\rm bit/symbol} $ as the one of the redundancy-free binary sequence $〈 q_ν 〉$.
The "Exercise 1.4" shows the considerable effort required to calculate the entropy approximation $H_3$. Moreover, $H_3$ still deviates significantly from the final value $H = 1 \,{\rm bit/symbol} $. A faster result is achieved if the AMI code is described by a Markov chain as explained in the next section.
Binary sources with Markov properties
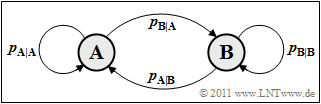
Sequences with statistical bindings between the sequence elements (symbols) are often modeled by $\text{Markov processes}$ where we limit ourselves here to first-order Markov processes. First we consider a binary Markov process $(M = 2)$ with the states (symbols) $\rm A$ and $\rm B$.
On the right, you can see the transition diagram for a first-order binary Markov process however, only two of the four transfer probabilities given are freely selectable, for example
- $p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}} = \rm Pr(A\hspace{0.01cm}|\hspace{0.01cm}B)$ ⇒ conditional probability that $\rm A$ follows $\rm B$ .
- $p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}} = \rm Pr(B\hspace{0.01cm}|\hspace{0.01cm}A)$ ⇒ conditional probability that $\rm B$ follows $\rm A$ .
For the other two transition probabilities: $p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} = 1- p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}$ and $p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} = 1- p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}
\hspace{0.05cm}.$
Due to the presupposed properties $\text{Stationarity}$ and $\text{Ergodicity}$ the following applies to the state or symbol probabilities:
- $$p_{\rm A} = {\rm Pr}({\rm A}) = \frac{p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}}{p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} \hspace{0.05cm}, \hspace{0.5cm}p_{\rm B} = {\rm Pr}({\rm B}) = \frac{p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}}{p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} \hspace{0.05cm}.$$
These equations allow first information–theoretical statements about the Markov processes:
- For $p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}} = p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}}$ the symbols are equally likely ⇒ $p_{\text{A}} = p_{\text{B}}= 0.5$. The first entropy approximation returns $H_1 = H_0 = 1 \hspace{0.05cm} \rm bit/symbol$, independent of the actual values of the (conditional) transition probabilities $p_{\text{A|B}}$ and $p_{\text{B|A}}$.
- But the source entropy $H$ as the limit value $($for $k \to \infty)$ of the "Entropy approximation of order $k$" ⇒ $H_k$ depends very much on the actual values of $p_{\text{A|B}}$ and $p_{\text{B|A}}$ and not only on their quotients. This is shown by the following example.
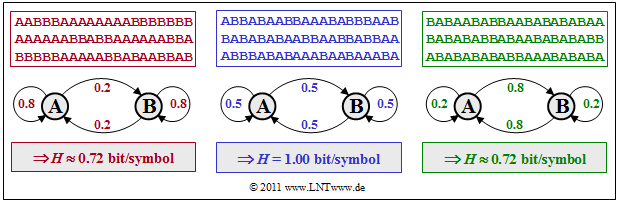
$\text{Example 6:}$ We consider three binary symmetric Markov sources that are represented by the numerical values of the symmetric transition probabilities $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} }$. For the symbol probabilities the following applies: $p_{\rm A} = p_{\rm B}= 0.5$, and the other transition probabilities have the values
- $$p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 1 - p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}B} }.$$
- The middle (blue) sequence with $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 0.5$ has the entropy $H ≈ 1 \hspace{0.1cm} \rm bit/symbol$. That means: In this special case there are no statistical bindings within the sequence.
- The left (red) sequence with $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 0.2$ has less changes between $\rm A$ and $\rm B$. Due to statistical dependencies between neighboring symbols the entropy is now smaller: $H ≈ 0.72 \hspace{0.1cm} \rm bit/symbol$.
- The right (green) symbol sequence with $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 0.8$ has the exact same entropy $H ≈ 0.72 \hspace{0.1cm} \rm bit/symbol$ as the red sequence. Here you can see many regions with alternating symbols $($... $\rm ABABAB$ ... $)$.
This example is worth noting:
- If you had not used the Markov properties of the red and green sequences, you would have reached the respective result $H ≈ 0.72 \hspace{0.1cm} \rm bit/symbol$ only after lengthy calculations.
- The following sections show that for a source with Markov properties the final value $H$ can be determined from the entropy approximations $H_1$ and $H_2$ alone. Likewise, all entropy approximations $H_1$ and $H_2$ can also be calculated from $H_k$ for $k$–tuples in a simple manner ⇒ $H_3$, $H_4$, $H_5$, ... $H_{100}$, ...
Simplified entropy calculation for Markov sources
We continue to assume the first-order symmetric binary Markov source. As in the previous section, we use the following nomenclature for
- the transition probabilities ⇒ $p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}}$, $p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}}$, $p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}A}}= 1- p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}}$, $p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}B}} = 1 - p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}}$,
- the ergodic probabilities ⇒ $p_{\text{A}}$ and $p_{\text{B}}$,
- the compound probabilities, for example ⇒ $p_{\text{AB}} = p_{\text{A}} - p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}}$.
We now compute the "Entropy of a two-tuple" (with the unit "bit/two-tuple"):
- $$H_2\hspace{0.05cm}' = p_{\rm A} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm A} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm B} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} + p_{\rm B} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}} \hspace{0.05cm}.$$
If one now replaces the logarithms of the products by corresponding sums of logarithms, one gets the result $H_2\hspace{0.05cm}' = H_1 + H_{\text{M}}$ with
- $$H_1 = p_{\rm A} \cdot (p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A})\cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p_{\rm A}} + p_{\rm B} \cdot (p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B})\cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p_{\rm B}} = p_{\rm A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p_{\rm A}} + p_{\rm B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p_{\rm B}} = H_{\rm bin} (p_{\rm A})= H_{\rm bin} (p_{\rm B}) \hspace{0.05cm},$$
- $$H_{\rm M}= p_{\rm A} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm A} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm B} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} + p_{\rm B} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}} \hspace{0.05cm}.$$
$\text{Conclusion:}$ Thus the »second entropy approximation« (with the unit "bit/symbol") is:
- $$H_2 = {1}/{2} \cdot {H_2\hspace{0.05cm}'} = {1}/{2} \cdot \big [ H_{\rm 1} + H_{\rm M} \big] \hspace{0.05cm}.$$
It is to be noted:
- The first summand $H_1$ ⇒ first entropy approximation depends only on the symbol probabilities.
- For a symmetrical Markov process ⇒ $p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}} = p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}} $ ⇒ $p_{\text{A}} = p_{\text{B}} = 1/2$ the result for this first summand is $H_1 = 1 \hspace{0.1cm} \rm bit/symbol$.
- The second summand $H_{\text{M}}$ must be calculated according to the second of the two upper equations.
- For a symmetrical Markov process you get $H_{\text{M}} = H_{\text{bin}}(p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}})$.
Now, this result is extended to the $k$–th entropy approximation. Here, the advantage of Markov sources over other sources is taken advantage of, that the entropy calculation for $k$–tuples is very simple. For each Markov source, the following applies
- $$H_k = {1}/{k} \cdot \big [ H_{\rm 1} + (k-1) \cdot H_{\rm M}\big ] \hspace{0.3cm} \Rightarrow \hspace{0.3cm} H_2 = {1}/{2} \cdot \big [ H_{\rm 1} + H_{\rm M} \big ]\hspace{0.05cm}, \hspace{0.3cm} H_3 ={1}/{3} \cdot \big [ H_{\rm 1} + 2 \cdot H_{\rm M}\big ] \hspace{0.05cm},\hspace{0.3cm} H_4 = {1}/{4} \cdot \big [ H_{\rm 1} + 3 \cdot H_{\rm M}\big ] \hspace{0.05cm},\hspace{0.15cm}{\rm usw.}$$
$\text{Conclusion:}$ With the boundary condition for $k \to \infty$, one obtains the actual source entropy
- $$H = \lim_{k \rightarrow \infty} H_k = H_{\rm M} \hspace{0.05cm}.$$
From this simple result important insights for the entropy calculation follow:
- For Markov sources it is sufficient to determine the entropy approximations $H_1$ and $H_2$. Thus, the entropy of a Markov source is
- $$H = 2 \cdot H_2 - H_{\rm 1} \hspace{0.05cm}.$$
- Through $H_1$ and $H_2$ all further entropy approximations $H_k$ are also fixed for $k \ge 3$ :
- $$H_k = \frac{2-k}{k} \cdot H_{\rm 1} + \frac{2\cdot (k-1)}{k} \cdot H_{\rm 2} \hspace{0.05cm}.$$
However, these approximations are not very important. Mostly only the limit value $H$ is of interest. For sources without Markov properties the approximations $H_k$ are calculated only to be able to estimate this limit value, i.e. the actual entropy.
Notes:
- In the "Exercise 1.5" the above equations are applied to the more general case of an asymmetric binary source.
- All equations in this section also apply to non-binary Markov sources $(M > 2)$ as shown in the next section.
Non-binary Markov sources
The following equations apply to each Markov source regardless of the symbol set size $M$:
- $$H = 2 \cdot H_2 - H_{\rm 1} \hspace{0.05cm},$$
- $$H_k = {1}/{k} \cdot \big [ H_{\rm 1} + (k-1) \cdot H_{\rm M}\big ] \hspace{0.05cm},$$
- $$ \lim_{k \rightarrow \infty} H_k = H \hspace{0.05cm}.$$
These equations allow the simple calculation of the entropy $H$ from the approximations $H_1$ and $H_2$.
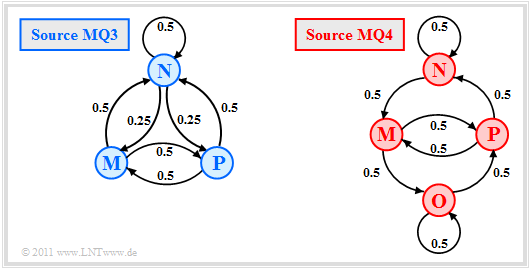
We now look at the transition diagrams sketched on the right:
- A ternary Markov source $\rm MQ3$ $(M = 3$, blue coloring$)$, and
- a quaternary Markov source $\rm MQ4$ $(M = 4$, red color$)$.
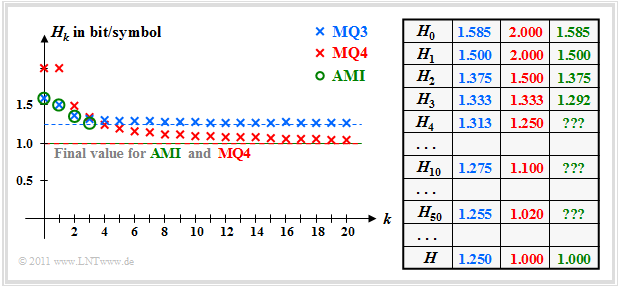
In "Exercise 1.6" the entropy approximations $H_k$ and the total entropy $H$ are calculated as the limit of $H_k$ for $k \to \infty$ . The results are shown in the following figure. All entropies specified there have the unit "bit/symbol".
These results can be interpreted as follows:
- For the ternary markov source $\rm MQ3$ the entropy approximations of $H_1 = 1.500$ above $H_2 = 1.375$ up to the limit $H = 1.250$ continuously decreasing. Because of $M = 3$ ⇒ $H_0 = 1.585$.
- For the quaternary Markov source $\rm MQ4$ one receives $H_0 = H_1 = 2.000$ (since four equally probable states) and $H_2 = 1.5$. From the $H_1$- and $H_2$-values all entropy approximations $H_k$ and the final value $H = 1.000$ can be calculated.
- The two models $\rm MQ3$ and $\rm MQ4$ were created during the attempt to calculate the "AMI code" to be described information–theoretically by Markov sources. The symbols $\rm M$, $\rm N$ and $\rm P$ stand for "minus", "zero" and "plus".
- The entropy approximations $H_1$, $H_2$ and $H_3$ of the AMI code (green markers) were calculated in the "Exercise 1.4". On the calculation of $H_4$, $H_5$, ... had to be omitted for reasons of effort. But the final value of $H_k$ for $k \to \infty$ ⇒ $H = 1.000$ is known.
- You can see that the Markov model $\rm MQ3$ for $H_0 = 1.585$, $H_1 = 1.500$ and $H_2 = 1.375$ yields exactly the same numerical values as the AMI code. On the other hand $H_3$ ⇒ $(1.333$ instead of $1.292)$ and especially the final value $H$ ⇒ $(1.250$ compared to $1.000)$.
- The model $\rm MQ4$ $(M = 4)$ differs from the AMI code $(M = 3)$ with respect to the decision content $H_0$ and also with respect to all entropy approximations $H_k$. Nevertheless, $\rm MQ4$ is the more suitable model for the AMI code, since the final value $H = 1,000$ is the same.
- The model $\rm MQ3$ yields entropy values that are too large, since the sequences $\rm PNP$ and $\rm MNM$ are possible here, which cannot occur in the AMI code. Already with the approximation $H_3$ the difference is slightly noticeable, in the final value $H$ even clearly $(1.25$ instead of $1)$.
In the model $\rm MQ4$ the state "Zero" was split into two states $\rm N$ and $\rm O$ (see upper right figure in this section):
- Here applies to the state $\rm N$: The current binary symbol $\rm L$ is encoded with the amplitude value $0$ (zero), as per the AMI rule. The next occurring $\rm H$ symbol, on the other hand, is displayed as $-1$ (minus), because the last symol $\rm H$ was encoded as $+1$ (plus).
- Also with the state $\rm O$ the current binary symbol $\rm L$ is represented with the ternary value $0$. In contrast to the state $\rm N$ however, the next occurring $\rm H$ symbol is now encoded as $+1$ (plus) since the last $\rm H$ symbol was encoded as $-1$ (minus).
$\text{Conclusion:}$
- The $\rm MQ4$ output sequence actually follows the rules of the AMI code and has entropy $H = 1.000 \hspace{0.15cm} \rm bit/symbol$.
- But because of the new state $\rm O$ now $H_0 = 2.000 \hspace{0.15cm} \rm bit/symbol$ $($against $1.585 \hspace{0.15cm} \rm bit/symbol)$ is clearly too large.
- Also all $H_k$ approximations are larger than with the AMI code. First for $k \to \infty$ the model $\rm MQ4$ and the AMI code match exactly: $H = 1.000 \hspace{0.15cm} \rm bit/symbol$.
Exercises for the chapter
Exercise 1.3: Entropy Approximations
Exercise 1.4: Entropy Approximations for the AMI Code
Exercise 1.4Z: Entropy of the AMI Code
Exercise 1.5: Binary Markov Source
Exercise 1.5Z: Symmetrical Markov Source
Exercise 1.6: Non-Binary Markov Sources
Exercise 1.6Z:Ternary Markov Source