Laplace Transform and p-Transfer Function

Considered system model

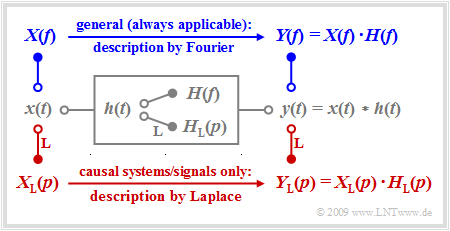
We consider a linear time-invariant system with the impulse response $h(t)$, whose input the signal $x(t)$ is applied to. The output signal $y(t)$ is then obtained as the convolution product $x(t) ∗ h(t)$.

General (also non-causal) and causal system model

For non-causal systems and signals, the first Fourier integral must always be applied to describe the spectral behavior and the following is valid for the output spectrum:

$$Y(f) = X(f) \cdot H(f) \hspace{0.05cm}.$$

The Fourier integral also continues to be valid for causal systems and signals, i.e. under the assumption

$$x(t) = 0 \hspace{0.2cm}{\rm{for}} \hspace{0.2cm} t<0\hspace{0.05cm},\hspace{0.2cm} h(t) = 0 \hspace{0.2cm}{\rm{for}} \hspace{0.2cm} t<0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} y(t) = 0 \hspace{0.2cm}{\rm{for}} \hspace{0.2cm} t<0 \hspace{0.05cm}.$$

In this case, however, there are significant advantages in applying the Laplace transformation while taking into account certain restrictions:

The systems treated in this way are always realizable by a circuit. The developer is not tempted to offer unrealistic solutions.
The Laplace transform $X_{\rm L}(p)$ is always a real function of the spectral variable $p$. The fact that this variable is derived from the multiplication of the physical angular frequency $ω = 2πf$ by the imaginary unit $\rm j$ according to $p = {\rm j} · 2πf$ does not matter for the user.
The implicit condition $x(t) = 0$ for $t < 0$ specifically allows for simpler analysis of transient
behavior after switching-on processes than with the Fourier integral.

Definition of the Laplace transformation

Starting from the first Fourier integral

$$X(f) = \int_{-\infty}^{+\infty} { x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f t}}\hspace{0.1cm}{\rm d}t,$$

the Laplace transformation is obtained directly by using the formal substitution $p = {\rm j} · 2πf$ for a causal time function $x(t) = 0 \ \ \ \text{for} \ \ \ t < 0.$

$\text{Definition:}$ The Laplace transform of a causal time function $x(t)$ is:

$$X_{\rm L}(p) = \int_{0}^{\infty} { x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-p t} }\hspace{0.1cm}{\rm d}t\hspace{0.05cm}, \hspace{0.3cm}{\rm briefly}\hspace{0.3cm} X_{\rm L}(p) \quad \bullet\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\circ\quad x(t)\hspace{0.05cm}.$$

The relationship between the Laplace transform $X_{\rm L}(p)$ and the physical spectrum $X(f)$ is often given as follows:

$$X(f) = X_{\rm L}(p) \Bigg |_{{\hspace{0.1cm} p\hspace{0.05cm}={\rm \hspace{0.05cm} j\hspace{0.05cm}2\pi \it f}}}.$$

However, if the signal $x(t)$ has periodic components and thus the spectral function $X(f)$ contains Dirac delta functions, then this equation is not applicable.
In this case, $p = α + {\rm j} · 2πf$ must be applied and then the limit $α → 0$ must be formed.

$\text{Example 1:}$ We assume the unilaterally and exponentially decreasing time function corresponding to the sketch in $\text{Example 1}$ of the chapter "Conclusions from the Allocation Theorem":

$$x(t) = \left\{ \begin{array}{c} 0 \\ 0.5 \\ {\rm e}^{-t/T} \end{array} \right.\quad \quad \begin{array}{c} {\rm{for} } \\ {\rm{for} } \\ {\rm{for} } \end{array}\begin{array}{*{20}c}{ t < 0\hspace{0.05cm},} \\ { t = 0\hspace{0.05cm},} \\{ t > 0\hspace{0.05cm}.} \end{array}$$

Thus, the Laplace transform is:

$$X_{\rm L}(p) = \int_{0}^{\infty} {\rm e}^{-t/T} \cdot {\rm e}^{-pt} \hspace{0.1cm}{\rm d}t= \frac {1}{p + 1/T} \cdot {{\rm e}^{-(p+1/T) \hspace{0.08cm}\cdot \hspace{0.08cm}t}}\hspace{0.15cm}\Bigg \vert_{t \hspace{0.05cm}=\hspace{0.05cm} 0}^{\infty}= \frac {1}{p + 1/T} \hspace{0.05cm} .$$

Considering $p = {\rm j} · 2πf$, the conventional spectral function with respect to $f$ is obtained:

$$X(f) = \frac {1}{{\rm j \cdot 2\pi \it f} + 1/T} = \frac {T}{1+{\rm j \cdot 2\pi \it fT}} \hspace{0.05cm} .$$

In contrast, if we consider the frequency response of a low-pass filter of first-order whose impulse response $h(t)$ differs from the above time function by the factor $1/T$, then the following holds for the Laplace transform and the Fourier transform, respectively:

$$H_{\rm L}(p)= \frac {1/T}{p + 1/T}= \frac {1}{1 + p \cdot T} \hspace{0.05cm} , \hspace{0.8cm}H(f) = \frac {1}{1+{\rm j \cdot 2\pi \it fT} } = \frac {1}{1+{\rm j} \cdot f/f_{\rm G} } \hspace{0.05cm} .$$

In this equation, the 3dB cut-off frequency $($German: "Grenzfrequenz" ⇒ "G"$)$ $f_{\rm G} = 1/(2πT)$ is used instead of the parameter $T$.

Some important Laplace correspondences

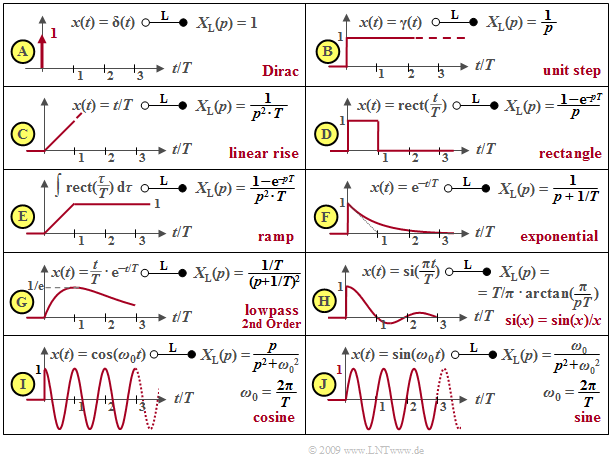
Some important Laplace correspondences are compiled subsequently. All time signals $x(t)$ considered here are assumed to be dimensionless. For this reason, $X_{\rm L}(p)$ then always has the unit "second" as an integral over time.

Table with some Laplace transforms

The Laplace transform of the Dirac delta function $δ(t)$ is $X_{\rm L}(p) = 1$ $($diagram $\rm A)$. $X_{\rm L}(p) = 1/p$ is obtained for the unit step function $γ(t)$ $($diagram $\rm B)$ by applying the integration theorem. From this the Laplace transform of the linearly increasing function $x(t) = t/T$ for $t > 0$ is obtained by multiplication by $1/(pT)$ $($diagram $\rm C)$.

The rectangular function can be generated from the subtraction of two step functions $γ(t)$ and $γ(t – T)$ separated by $T$ so that the Laplace transform $X_{\rm L}(p) = (1 – {\rm e}^{–pT})/p$ is obtained according to the shifting theorem $($diagram $\rm D)$. By integration the ramp function or after multiplication by $1/(pT)$ its Laplace transform is obtained from it $($diagram $\rm E)$.

The exponential function $($diagram $\rm F)$ has already been considered on the last page . Considering the factor $1/T$, this is at the same time the impulse response of a low-pass filter of first-order. The $p$–spectral function of a low-pass filter of second-order with the time function $x(t) = t/T · {\rm e}^{–t/T}$ (diagram $\rm G$) is obtained by squaring.

In addition to the causal $\rm si$–function $($diagram $\rm H)$, the Laplace transforms of the causal cosine and sine functions $($diagrams $\rm I$ and $\rm J)$, which result in $p/(p^2 + ω_0^2)$ and $ω_0/(p^2 + ω_0^2)$ resp., are also given in the table. Here, $ω_0 = 2πf_0 = 2π/T$ denotes the so-called angular frequency.

Pole-zero representation of circuits

Any linear time-invariant system $\rm (LTI)$ which can be realized by a circuit of discrete time-constant components such as

resistances $(R)$,
capacitances $(C)$,
inductances $(L)$ and
amplifier elements,

has a fractional-rational $p$–transfer function:

$$H_{\rm L}(p)= \frac {A_Z \cdot p^Z +\text{...} + A_2 \cdot p^2 + A_1 \cdot p + A_0} {B_N \cdot p^N +\text{...} \ + B_2 \cdot p^2 + B_1 \cdot p + B_0}= \frac {Z(p)}{N(p)} \hspace{0.05cm} .$$

All coefficients of the numerator ⇒ $A_Z, \text{...} \ , A_0$ and of the denominator ⇒ $B_N, \text{...} , B_0$ are real. Furthermore:

$Z$ denotes the degree of the numerator polynomial $Z(p)$,
$N$ denotes the degree of the denominator polynomial $N(p)$.

$\text{Equivalent pole-zero representation:}$ The following can be formulated for the $p$–transfer function, too:

$$H_{\rm L}(p)= K \cdot \frac {\prod\limits_{i=1}^Z p - p_{\rm o i} } {\prod\limits_{i=1}^N p - p_{\rm x i} }= K \cdot \frac {(p - p_{\rm o 1})(p - p_{\rm o 2})\cdot \text{...} \ \cdot (p - p_{ {\rm o} \hspace{-0.03cm} Z})} {(p - p_{\rm x 1})(p - p_{\rm x 2})\cdot \text{...} \cdot (p - p_{ {\rm x} \hspace{-0.03cm} N})} \hspace{0.05cm} .$$

The $Z + N + 1$ parameters signify:

$K = A_Z/B_N$ is a constant factor. If $Z = N$ holds, then this is dimensionless.
The solutions of the equation $Z(p) = 0$ result in the $Z$ "zeros" $p_{\rm o1},\text{...} \ , p_{\rm oZ}$ of $H_{\rm L}(p)$.
The zeros of the denominator polynomial $N(p)$ yield the $N$ pole locations (or "poles" for short).

The transformation is unique. This can be seen from the fact that the $p$–transfer function is also determined only by $Z + N + 1$ free parameters according to the first equation since one of the coefficients $A_Z, \text{...} \ , A_0, B_N, \text{...} \ , B_0$ can be normalized to $1$ without changing the quotient.

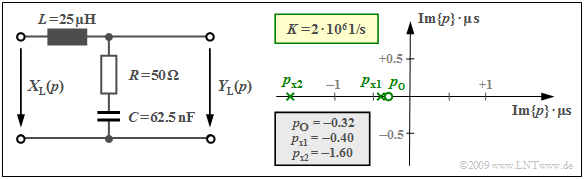
Considered two-port network and associated pole-zero diagram

$\text{Example 2:}$ We consider the drawn two-port network with an inductance $L$ $($complex resistance $pL)$ in the longitudinal branch as well as the series connection of an ohmic resistance $R$ and a capacitance $C$ with the complex resistance $1/(pC)$ in the transverse branch.

Thus, the $p$–transfer function is:

$$H_{\rm L}(p)= \frac {Y_{\rm L}(p)} {X_{\rm L}(p)}= \frac {R + {1}/{(pC)} } {pL + R +{1}/{(pC)} }$$

$$\Rightarrow \hspace{0.3cm} H_{\rm L}(p)= \frac {1 + p \cdot{RC} } {1 + p \cdot{RC}+ p^2 \cdot{LC} } \hspace{0.05cm} .$$

If $p = {\rm j} · 2πf$ is set, then the Fourier transfer function (or the frequency response) is obtained. If the numerator and denominator in the above equation are divided by $LC$, then the following is obtained:

$$H_{\rm L}(p)= \frac {R} {L}\cdot \frac {p + {1}/{(RC)} } {p^2 + {R}/ {L}\cdot p + {1}/{(LC)} }= K \cdot \frac {p - p_{\rm o } } {(p - p_{\rm x 1})(p - p_{\rm x 2})} \hspace{0.05cm} .$$

In the right-hand side of the equation, the transfer function $H_{\rm L}(p)$ is given in pole-zero notation. By comparison of coefficients the following values are obtained for $R = 50 \ \rm Ω$, $L = 25\ \rm µ H$ and $C = 62.5 \ \rm nF$ :

the constant $K = R/L = 2 · 10^6 \cdot 1/{\rm s}$,
the zero $p_{\rm o} = -1/(RC) = -0.32 · 10^6 \cdot 1/{\rm s},$
the two poles $p_{\rm x1}$ and $p_{\rm x2}$ as the solution of the equation

$$p^2 + \frac {R} {L}\cdot p + \frac{1}{LC} = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm x 1,\hspace{0.05cm}2 }= -\frac {R} {2L}\pm \sqrt{\frac {R^2} {4L^2}- \frac{1}{LC} }$$

$$\Rightarrow \hspace{0.3cm} p_{\rm x 1,\hspace{0.05cm}2 }= -10^6 \cdot {1}/{\rm s} \pm \sqrt{10^{12} \cdot {1} /{\rm s^2}-0.64 \cdot 10^{12} \cdot {1}/ {\rm s^2} }\hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_{\rm x 1 }= -0.4 \cdot 10^6\cdot {1}/ {\rm s},\hspace{0.2cm}p_{\rm x 2 }= -1.6 \cdot 10^6\cdot {1}/ {\rm s} \hspace{0.05cm} .$$

In the above graph, the pole-zero diagram is given on the right-hand side.

The two axes denote the real and imaginary parts of the variable $p$, each normalized to the value $10^6 · \rm 1/s\; (= 1/µs)$.
The zero at $p_{\rm o} =\, –0.32$ can be seen as a circle and the poles at $p_{\rm x1} = \,–0.4$ and $p_{\rm x2} = \,–1.6$ as crosses.

Properties of poles and zeros

The transfer function $H_{\rm L}(p)$ of any realizable circuit is fully described by $Z$ "zeros" and $N$ "poles" together with a constant $K$ where the following restrictions apply:

$Z ≤ N$ always holds. The $p$–transfer function would also be "infinitely large" with $Z > N$ in the limiting case for $p → ∞$ (i.e. for very high frequencies).
The zeros $p_{\rm oi}$ and the poles $p_{ {\rm x}i}$ are generally complex, and have like $p$ the unit $\rm 1/s$. If $Z < N$ holds, then the constant $K$ has also a unit.
The poles and zeros can be real as shown in the last example. If they are complex, then two poles and two zeros always occur as complex conjugates, respectively, since $H_{\rm L}(p)$ always represents a real fractional-rational function.
All poles lie in the left half-plane or on the imaginary axis (limiting case). This property follows from the required and assumed causality together with the fundamental function theory, which will be stated in the next chapter.
Zeros can occur in both the left and right $p$–half-planes or also on the imaginary axis. An example of zeros in the right half-plane can be found in Exercise 3.4Z, which deals with all-pass filters.
In so-called "minimum-phase systems", not only poles are forbidden in the right $p$–half-plane but also zeros. The real part of all singularities here is never positive.

These properties are now illustrated by three examples.

$\text{Example 3:}$ Starting from the two-port network $(L$ in the longitudinal branch, $R$ and $C$ in the transverse branch$)$ the characteristic quantities of the transfer function can be given as follows:

$$K = 2A, \hspace{0.2cm}p_{\rm x 1,\hspace{0.05cm}2 }= -A \pm \sqrt{A^2-B^2}, \hspace{0.2cm}p_{\rm o }= - \frac{B^2}{2A} \hspace{0.05cm} \hspace{0.2cm} {\rm with } \hspace{0.2cm} A = \frac {R} {2L}, \hspace{0.2cm}B = \frac{1}{\sqrt{LC} } \hspace{0.05cm}.$$

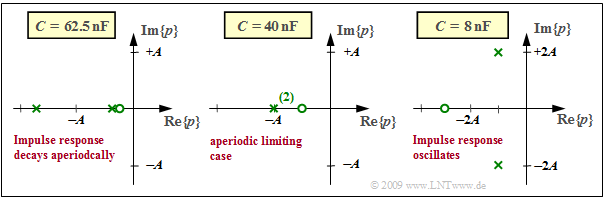
The graph shows three different diagrams with different capacitance values $C$. $R = 50 \ \rm Ω$ and $L = 25 \ \rm µ H$ always hold. The axes are normalized to the variable $A = R/(2L) = 10^6 · \rm 1/s$ and the constant factor in each case is $K = 2A = 2 · 10^6 · \rm 1/s.$

Location of the zero and the poles for $Z = 1$ and $N = 2$

For $B < A$, two real poles and a zero to the right of $-A/2$ are obtained. The following arises as a result for $C = 62.5 \ \rm nF$ ⇒ $ {B}/ {A}= 0.8 $ (left diagram):

$$ p_{\rm x 1}/A = -0.4 , \hspace{0.2cm}p_{\rm x 2}/A= -1.6 , \hspace{0.2cm}p_{\rm o}/A= -0.32 \hspace{0.05cm} .$$

For $B > A$, two conjugate-complex poles and a zero to the left of $-A/2$ are obtained. For $C = 8 \ \rm nF$ ⇒ $ {B}/ {A}= \sqrt{5} $ (right diagram):

$$p_{\rm x 1,\hspace{0.05cm}2 }/A= -1\pm {\rm j}\cdot 2,\hspace{0.2cm}p_{\rm o}/A\approx -2.5 \hspace{0.05cm} .$$

The case $A = B$ leads to a real double pole and a zero at $– A/2$. For $C = 400 \ \rm nF$ ⇒ $ {B}/ {A}= 1 $ (middle diagram):

$$ p_{\rm x 1}/A= p_{\rm x 2}/A= -1, \hspace{0.2cm}p_{\rm o}/A= -0.5 \hspace{0.05cm} .$$

The impulse responses $h(t)$ are obtained according to the following chapter Inverse Laplace Transform as follows:

For the left constellation, $h(t)$ is aperiodically decaying.
For the right constellation, $h(t)$ is attenuated-oscillatory.
The middle constellation is called the critically-damped case.

Graphical determination of attenuation and phase

Output diagram for the computation
of attenuation and phase

The $p$–transfer function is given in pole-zero notation:

$$H_{\rm L}(p)= K \cdot \frac {\prod\limits_{i=1}^Z (p - p_{\rm o i})} {\prod\limits_{i=1}^N (p - p_{\rm x i})}= K \cdot \frac {(p - p_{\rm o 1})(p - p_{\rm o 2})\cdot \text{...} \cdot (p - p_{ {\rm o} \hspace{-0.03cm} Z})} {(p - p_{\rm x 1})(p - p_{\rm x 2})\cdot \text{...} \cdot (p - p_{ {\rm x} \hspace{-0.03cm} N})} \hspace{0.05cm} .$$

The conventional frequency response $H(f)$ is obtained by replacing the argument $p$ of $H_{\rm L}(p)$ by ${\rm j} \cdot 2πf$ :

$$H(f)= K \cdot \frac {({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{\rm o 1})({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{\rm o 2})\cdot \text{...} \cdot ({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{ {\rm o} \hspace{-0.03cm} Z})} {({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{\rm x 1})({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{\rm x 2})\cdot \text{...}\cdot ({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{ {\rm x} \hspace{-0.03cm} N})} \hspace{0.05cm} .$$

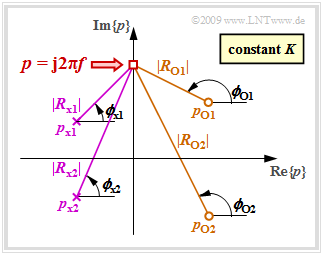
We now consider a fixed frequency $f$ and describe the distances and angles of all "zeros" (circles) by vectors:

$$R_{ {\rm o} i} = {\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{ {\rm o} i}= |R_{{\rm o} i}| \cdot {\rm e}^{\hspace{0.03cm}{\rm j}\hspace{0.03cm}\cdot\hspace{0.03cm}\phi_{ {\rm o} i} }, \hspace{0.3cm}i= 1, \text{...}\ , Z \hspace{0.05cm} .$$

We proceed in the same way for the "poles" (crosses):

$$R_{ {\rm x} i} = {\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{ {\rm x} i}= |R_{ {\rm x} i}| \cdot {\rm e}^{\hspace{0.03cm}{\rm j}\hspace{0.03cm}\cdot\hspace{0.03cm}\phi_{ {\rm x} i} }, \hspace{0.3cm}i= 1, \text{...}\ , N \hspace{0.05cm} .$$

The graph shows the magnitudes and phase angles for a system

with $Z = 2$ zeros (circles) in the right half-plane
and $N = 2$ poles (crosses) in the left half-plane.

Moreover, the constant $K$ is also to be considered.

The following can be written for the frequency response with this vector representation:

$$H(f)= K \cdot \frac {|R_{ {\rm o} 1}| \cdot |R_{ {\rm o} 2}|\cdot ... \cdot |R_{ {\rm o} \hspace{-0.03cm} Z}|} {|R_{ {\rm x} 1}| \cdot |R_{ {\rm x} 2}|\cdot \text{...} \cdot |R_{ {\rm x} \hspace{-0.03cm} N}|} \cdot {\rm e^{\hspace{0.03cm}{\rm j} \hspace{0.05cm}\cdot [ \phi_{ {\rm o} 1}\hspace{0.1cm}+ \hspace{0.1cm}\phi_{ {\rm o} 2} \hspace{0.1cm}+ \hspace{0.1cm}\hspace{0.1cm}\text{...}. \hspace{0.1cm} + \hspace{0.1cm}\phi_{ {\rm o} \hspace{-0.03cm}{\it Z}}\hspace{0.1cm}- \hspace{0.1cm}\phi_{ {\rm x} 1}\hspace{0.1cm}- \hspace{0.1cm}\phi_{ {\rm x} 2} \hspace{0.1cm}- \hspace{0.1cm}... \hspace{0.1cm} - \hspace{0.1cm} \phi_{ {\rm x} \hspace{-0.03cm}{\it N} }]} } \hspace{0.05cm} .$$

If $H(f)$ is expressed by the attenuation function $a(f)$ and the phase function $b(f)$ according to the generally valid relation $H(f) = {\rm e}^{-a(f)\hspace{0.05cm}- \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}b(f)}$, then the following result is obtained by comparing with the above equation:

With a suitable normalization of all dimensional quantities the following holds for the attenuation function in Neper $(1 \ \rm Np$ corresponds to $8.686 \ \rm dB)$:

$$a(f) = -{\rm ln} \hspace{0.1cm} K + \sum \limits_{i=1}^N {\rm ln} \hspace{0.1cm} |R_{ {\rm x} i}|- \sum \limits_{i=1}^Z {\rm ln} \hspace{0.1cm} |R_{ {\rm o} i}| \hspace{0.05cm} .$$

The phase function in radian $\rm (rad)$ arises as a result according to the upper sketch and is

$$b(f) = \phi_K + \sum \limits_{i=1}^N \phi_{ {\rm x} i}- \sum \limits_{i=1}^Z \phi_{ {\rm o} i}\hspace{0.2cm}{\rm with} \hspace{0.2cm} \phi_K = \left\{ \begin{array}{c} 0 \\ \pi \end{array} \right. \begin{array}{c} {\rm{for} } \\ {\rm{for} } \end{array}\begin{array}{*{20}c} { K > 0\hspace{0.05cm},} \\ { K <0\hspace{0.05cm}.} \end{array}$$

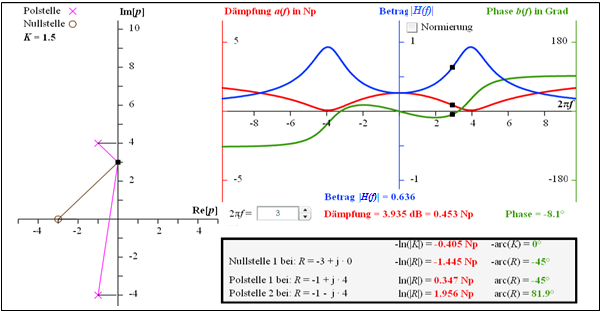
For the computation of the attenuation and phase functions (screen capture of the program "Causal Systems & Laplace Transformation" in an earlier German version)

$\text{Example 4:}$ The graphic illustrates the calculation

of the attenuation function $a(f)$ ⇒ red curve, and
of the phase function $b(f)$ ⇒ green curve

of a two-port network which is defined by the factor $K = 1.5$, one zero at $-3$ and two poles at $–1 \pm {\rm j} · 4$.

The given numerical values are valid for the frequency $2πf = 3$:

$$a \big [f = {3}/({2\pi}) \big ] = 0.453\,\,{\rm Np}= 3.953\,\,{\rm dB}$$

$$\Rightarrow \hspace{0.4cm}\big \vert H \big [f = {3}/({2\pi}) \big ]\big \vert = 0.636,$$

$$ b\big [f = {3}/({2\pi}) \big ] = -8.1^\circ \hspace{0.05cm} .$$

The derivation of these numerical values is illustrated in the framed block. For the magnitude frequency response $\vert H(f)\vert$ ⇒ blue curve, a bandpass-like curve shape is obtained with

$$\vert H(f = 0)\vert \approx 0.25\hspace{0.05cm},$$

$$\vert H(f = {4}/(2\pi)\vert \approx 0637\hspace{0.05cm},$$

$$\vert H(f \rightarrow \infty)\vert= 0 \hspace{0.05cm}.$$