Signal Representation/Fast Fourier Transform (FFT)

1. Signal Representation
2. Time and Frequency-Discrete Signal Representation
3. Fast Fourier Transform (FFT)

• Previous page
• Next page

• Previous page
• Next page

Complexity of DFT and IDFT

A disadvantage of the direct calculation of the  (generally complex) DFT sequences

$$\langle \hspace{0.1cm}D(\mu)\hspace{0.1cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm}d(\nu)\hspace{0.1cm} \rangle$$

according to the equations given in chapter  Discrete Fourier Transform  $\rm (DFT)$  is the large computational cost.

We consider as an example the DFT, i.e. the calculation of the  $D(\mu)$  coefficients from the  $d(\nu)$  coefficients:

$$N \cdot D(\mu) = \sum_{\nu = 0 }^{N-1} d(\nu) \cdot {w}^{\hspace{0.03cm}\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} = d(0) \cdot w^{\hspace{0.03cm}0} + d(1) \cdot w^{\hspace{0.03cm}\mu}+ d(2) \cdot w^{\hspace{0.03cm}2\mu}+\hspace{0.05cm}\text{ ...} \hspace{0.05cm}+ d(N-1) \cdot w^{\hspace{0.03cm}(N-1)\cdot \mu}.$$

The computational effort required for this is to be estimated, assuming that the powers of the complex rotation factor  $w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi/N}$  already exist in real and imaginary part form in a lookup table.  To calculate a single coefficient, one then needs  $N-1$  complex multiplications and as many complex additions, observing:

• Each complex addition requires two real additions:

$$(R_1 + {\rm j} \cdot I_1) + (R_2 + {\rm j} \cdot I_2) = (R_1 + R_2) + {\rm j} \cdot (I_1 + I_2)\hspace{0.05cm}.$$

• Each complex multiplication requires four real multiplications and two real additions  (a subtraction is treated as an addition):

$$(R_1 + {\rm j} \cdot I_1) (R_2 + {\rm j} \cdot I_2) = (R_1 \cdot R_2 - I_1 \cdot I_2) + {\rm j} \cdot (R_1 \cdot I_2 + R_2 \cdot I_1)\hspace{0.05cm}.$$

• Thus, the following number of real multiplications and the number of real additions are required to calculate all $N$ coefficients in total:

$$M = 4 \cdot N \cdot (N-1),$$

$$A = 2 \cdot N \cdot (N-1)+2 \cdot N \cdot (N-1)=M \hspace{0.05cm}.$$

• In today's computers, multiplications and additions/subtractions need about the same computing time.  It is sufficient to consider the total number  $\mathcal{O} = M + A$  of all operations:

$$\mathcal{O} = 8 \cdot N \cdot (N-1) \approx 8 \cdot N^2\hspace{0.05cm}.$$

$\text{Conclusion:}$ 

• For a  Discrete Fourier Transform  (DFT) with  $N = 1000$  one already needs almost eight million arithmetic operations.  The same applies to an IDFT.
• With  $N =16$  still  $1920$  computational operations are required.

If the parameter  $N$  is a power to the base  $2$, more computationally efficient algorithms can be applied.  The multitude of such methods known from the literature are summarised under the collective term  $\text{Fast Fourier Transform}$  - abbreviated  $\text{FFT}$.  All these methods are based on the  "superposition theorem"  of the DFT.

Superposition theorem of the DFT

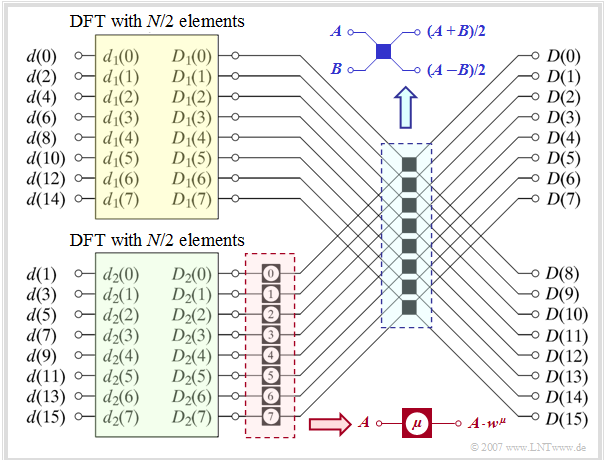
The graph illustrates the so-called  "superposition theorem"  of the DFT using the example of $N = 16$.  Shown here is the transition from the time domain to the spectral domain, i.e. the calculation of the spectral domain coefficients from the time domain coefficients:   $\langle \hspace{0.1cm}D(\mu)\hspace{0.1cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm} d(\nu) \hspace{0.1cm}\rangle.$

Superposition theorem of the DFT

The algorithm described thereby is characterised by the following steps:

• The sequence  $\langle \hspace{0.1cm}d(\nu)\hspace{0.1cm}\rangle$  of length  $N$  is divided into two subsequences$\langle \hspace{0.1cm} d_1(\nu)\hspace{0.1cm}\rangle$  and  $\langle \hspace{0.1cm} d_2(\nu)\hspace{0.1cm}\rangle$  each of half length  (highlighted in yellow and green respectively in the garafic).  With  $0 \le \nu \lt N/2$  one thus obtains the sequence elements

$$d_1(\nu) = d(2\nu), $$

$$d_2(\nu) = d(2\nu+1) \hspace{0.05cm}.$$

• The initial sequences  $\langle \hspace{0.1cm}D_1(\mu )\hspace{0.1cm}\rangle$  and  $\langle \hspace{0.1cm}D_2(\mu )\hspace{0.1cm}\rangle$  of the two sub-blocks result from this each by its own DFT,  but now only with half length  $N/2 = 8$:

$$\langle \hspace{0.1cm}D_1(\mu) \hspace{0.1cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N/2)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm}d_1(\nu) \hspace{0.1cm}\rangle , $$

$$ \langle \hspace{0.1cm}D_2(\mu)\hspace{0.1cm} \rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N/2)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm}d_2(\nu) \hspace{0.1cm}\rangle \hspace{0.05cm}.$$

• The initial values  $\langle \hspace{0.1cm} D_2(\mu )\hspace{0.1cm}\rangle$  of the lower (green) DFT $($with  $0 \le \mu \lt N/2)$  are then changed in the block outlined in red by complex rotation factors with respect to phase:

$$D_2(\mu) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}D_2(\mu) \cdot w^{\hspace{0.04cm}\mu}, \hspace{0.2cm}{\rm with}\hspace{0.1cm}w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi/N} \hspace{0.05cm}.$$

• Each single  Butterfly  in the blue bordered block (in the middle of the graph) yields two elements of the searched sequence by addition or subtraction.  With  $0 \le \mu \lt N/2$  applies:

$$D(\mu) = {1}/{2}\cdot \big[D_1(\mu) + D_2(\mu) \cdot w^{\hspace{0.04cm}\mu}\big],$$

$$D(\mu +{N}/{2}) = {1}/{2}\cdot \big[D_1(\mu) - D_2(\mu) \cdot w^{\hspace{0.04cm}\mu}\big]\hspace{0.05cm}.$$

This first application of the superposition theorem thus roughly halves the computational effort.

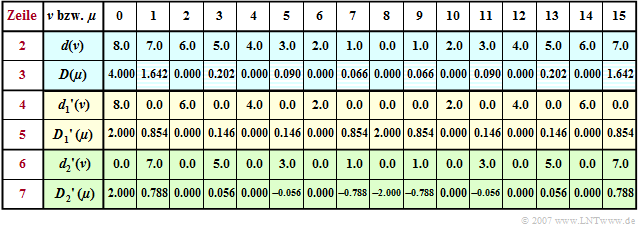
$\text{Example 1:}$  Let the DFT coefficients  $d(\nu)$  for the description of the time course be  "triangular"  according to  line 2  of the following table.  Note here the periodic continuation of the DFT, so that the linear increase for  $t \lt 0$  is given by the coefficients  $d(8), \hspace{0.05cm}\text{ ...} \hspace{0.05cm}, d(15)$.

Applying the DFT algorithm with  $N = 16$  one obtains the spectral coefficients  $D(\mu )$  given in  line 3  which would be equal  $D(\mu ) = 4 \cdot \text{si}^2(\pi \cdot \mu/2)$  if the aliasing error were neglected.  We can see that the aliasing error only affects the odd coefficients (shaded boxes). For example, $D(1) = 16/ \pi^2 \approx 1.621\neq 1.642$  should be.

Result table for  $\text{Example 1}$  for the superposition theorem of the DFT

If we split the total sequence  $\langle \hspace{0.1cm}d(\nu)\hspace{0.1cm}\rangle$  into two subsequences such that the first subsequence  $\langle \hspace{0.1cm}{d_1}'(\nu)\hspace{0.1cm}\rangle$   ⇒   yellow marked has only even coefficients  $(\nu = 0, 2, \hspace{0.03cm}\text{ ...} \hspace{0.1cm}, N–2)$  and the second subsequence  $\langle \hspace{0.1cm}{d_2}'(\nu)\hspace{0.1cm}\rangle$  ⇒   green marked contains only odd coefficients  $(\nu = 1, 3, \hspace{0.03cm}\text{ ...} \hspace{0.1cm} , N-1)$  and all others are set to zero.  The corresponding sequences in the spectral domain are obtained:

$$ \langle \hspace{0.1cm}{D_1}'(\mu)\hspace{0.1cm} \rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm} {d_1}'(\nu) \hspace{0.1cm}\rangle , $$

$$ \langle \hspace{0.1cm}{D_2}'(\mu) \hspace{0.1cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle\hspace{0.1cm} {d_2}'(\nu) \rangle \hspace{0.1cm}\hspace{0.05cm}.$$

In the yellow or green lines  $4\hspace{0.05cm}\text{ ...} \hspace{0.05cm}7$  you can see:

• Because of  $d(\nu) = {d_1}'(\nu) + {d_2}'(\nu)$  also holds 

$$D(\mu ) = {D_1}'(\mu ) + {D_2}'(\mu ).$$

This can be justified, for example, with the  Addition Theorem of Linear Systems.

• The period of the sequence  $\langle \hspace{0.1cm}{D_1}'(\mu )\hspace{0.1cm}\rangle$  due to the zeroing of every second time coefficient is now  $N/2$  unlike the period  $N$  of the sequence  $\langle \hspace{0.1cm} D(\mu )\hspace{0.1cm}\rangle$:

$${D_1}'(\mu + {N}/{2}) ={D_1}'(\mu)\hspace{0.05cm}.$$

• The sequence  $\langle \hspace{0.1cm} {D_2}'(\mu )\hspace{0.1cm}\rangle$  additionally contains a phase factor  (shift by one sample)  which causes a sign change of two coefficients separated by  $N/2$:

$${D_2}'(\mu + {N}/{2}) = - {D_2}'(\mu)\hspace{0.05cm}.$$

• The calculation of  $\langle \hspace{0.1cm}{D_1}'(\mu )\hspace{0.1cm}\rangle$  and  $\langle \hspace{0.1cm} {D_2}'(\mu )\hspace{0.1cm}\rangle$  is, however, in each case as time-consuming as the determination of  $\langle \hspace{0.1cm}D(\mu )\hspace{0.1cm}\rangle$, since  $\langle \hspace{0.1cm}{d_1}'(\nu)\hspace{0.1cm}\rangle$  and  $\langle \hspace{0.1cm}{d_2}'(\nu)\hspace{0.1cm}\rangle$  also consist of  $N$  elements, even if half of them are zeros.

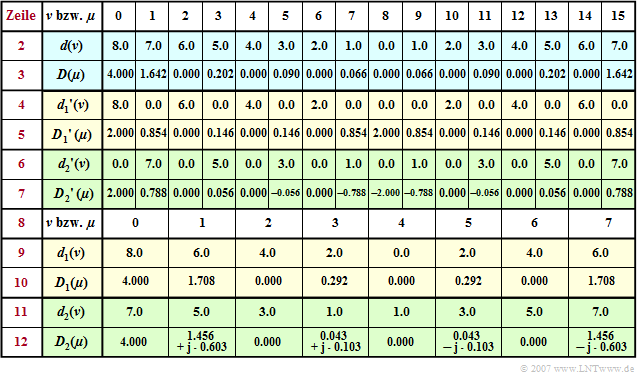
$\text{Example 2:}$  To continue the first example, the previous table is now extended by the rows  $8$  to  $12$ .

Result table for  $\text{Example 2}$  for the superposition theorem of the DFT

Omitting the coefficients  ${d_1}'(\nu) = 0$  with odd indices and  ${d_2}'(\nu) = 0$  with even indices, we arrive at the subsequences  $\langle \hspace{0.1cm}d_1(\nu)\hspace{0.1cm}\rangle$  and  $\langle \hspace{0.1cm}d_2(\nu)\hspace{0.1cm}\rangle$  corresponding to lines  $9$  and  $11$ . You can see:

• The time sequences  $\langle \hspace{0.1cm}{d_1}(\nu )\hspace{0.1cm}\rangle$  and  $\langle \hspace{0.1cm}{d_2}(\nu )\hspace{0.1cm}\rangle$  exhibit as well as the corresponding spectral sequences  $\langle \hspace{0.1cm}{D_1}(\mu )\hspace{0.1cm}\rangle$  and  $\langle \hspace{0.1cm}{D_2}(\mu )\hspace{0.1cm}\rangle$  only have the dimension $(N/2)$.
• A comparison of the lines  $5$,  $7$,  $10$  and  $12$  shows the following relationship for  $0 \le \mu \lt N/2$ :

$${D_1}'(\mu) = {1}/{2}\cdot {D_1}(\mu)\hspace{0.05cm},$$

$$ {D_2}'(\mu) = {1}/{2}\cdot {D_2}(\mu)\cdot w^{\hspace{0.04cm}\mu}\hspace{0.05cm}.$$

• Correspondingly, for  $N/2 \le \mu \lt N$:

$${D_1}'(\mu) = {1}/{2}\cdot {D_1}(\mu - {N}/{2})\hspace{0.05cm},$$

$$ {D_2}'(\mu) = {1}/{2}\cdot {D_2}(\mu {-} {N}/{2})\cdot w^{\hspace{0.04cm}\mu}$$

$$ \Rightarrow \hspace{0.3cm}{D_2}'(\mu) = { - } {1}/{2}\cdot {D_2}(\mu-N/2)\cdot w^{\hspace{0.04cm}\mu {-} N/2}\hspace{0.05cm}.$$

• For example, with  $N = 16$   ⇒   $w = {\rm e}^{ - {\rm j}\hspace{0.04cm} \cdot \hspace{0.04cm}\pi/8}$  for the indices  $\mu = 1$  respectively  $\mu = 9$: 

$${D_1}'(1) = {1.708}/{2} = 0.854,\hspace{0.8cm} {D_2}'(1) ={1}/{2}\cdot (1.456 + {\rm j} 0.603) \cdot {\rm e}^{ - {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \pi/8} = 0.788$$

$$\Rightarrow D(1) = {D_1}'(1)+ {D_2}'(1)= 1.642 \hspace{0.05cm}.$$

$${D_9}'(1) = {1.708}/{2} = 0.854,\hspace{0.8cm} {D_2}'(9) = - {1}/{2}\cdot (1.456 + {\rm j} 0.603) \cdot {\rm e}^{ - {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \pi/8} = - 0.788$$

$$\Rightarrow D(9) = {D_1}'(9)+ {D_2}'(9)= 0.066 \hspace{0.05cm}.$$

$\text{Conclusion:}$ 

• This first application of the superposition theorem almost halves the computational effort.
• Instead of  $\mathcal{O}= 1920$  one only needs  $\mathcal{O} = 2 - 448 + 8 \cdot (4+2) + 16 \cdot 2 = 976$  real operations.
• The first summand accounts for the two DFT calculations with  $N/2 = 8$.
• The remainder is needed for the eight complex multiplications and the  $16$  complex additions and subtractions, respectively.

Radix-2 algorithm according to Cooley and Tukey

Like other FFT algorithms, the method presented herenbsp; [CT65]  from   James W. Cooley  and  John W. Tukey  on the superposition theorem of the DFT.  It only works if the number of interpolation points is a power of two.

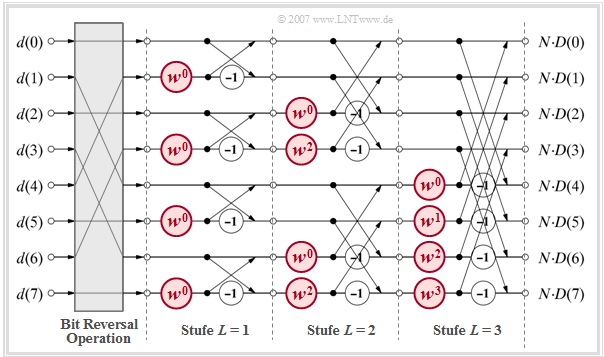
The diagram illustrates the algorithm for  $N = 8$, again showing the transformation from the time to the frequency domain.

Radix-2 algorithm (flow diagram)

• Before the FFT algorithm, the input values  $d(0), \hspace{0.05cm}\text{...} \hspace{0.1cm}, d( N - 1)$  have to be reordered in the grey block  "Bit Reversal Operation".
• The computation is done in  $\text{log}_2 N = 3$  stages, where in each stage  $N/2 = 4$  equal computations are performed with different  $\mu$–values as exponent of the complex rotation factor.  Such a basic operation is called  $\text{butterfly}$.
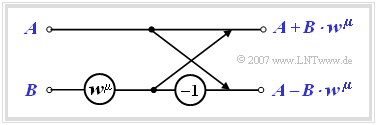
• Each butterfly calculates from two  (generally complex)  input variables  $A$  and  $B$  the two output variables  $A + B \cdot w^{\mu}$  and  $A - B \cdot w^{\mu}$  according to the following sketch.

Butterfly of the DFT algorithm

$\text{Conclusion:}$  The complex spectral coefficients  $D(0), \hspace{0.05cm}\text{...} \hspace{0.1cm}, D( N - 1)$  are obtained at the output of the last stage after division by  $N$.

• As shown in  Exercise 5.5Z  compared to the DFT, this results in a much shorter computation time, for example for  $N = 1024$  by more than a factor  $150$.

• The inverse DFT for calculating the time coefficients from the spectral coefficients is done with the same algorithm and only slight modifications.

Radix-2 algorithm (C program)

$\text{Example 3:}$  Finally, the C program  $\text{fft(N, Re, Im)}$  according to the Radix-2 algorithm described above is given:

• The two float arrays  "Re"  and  "Im"  contain the  $N$  real and imaginary parts of the complex time coefficients  $d(0)$, ... , $d( N - 1)$.
• In the same fields  "Re"  and  "Im"  the complex coefficients  $D(0)$, ... , $D( N - 1)$  are returned to the main program.
• Due to the  "in-place"  programming,   $N$  complex memory space is thus sufficient for this algorithm but only if the input values are reordered at the beginning.
• This is done by the program  "bit-reversal", where the contents of  ${\rm Re}( \nu)$  and  ${\rm Im}( \nu)$  are entered into the elements  ${\rm Re}( \kappa)$  and  ${\rm Im}( \kappa)$.  The  $\text{Example 4}$  illustrates this procedure.

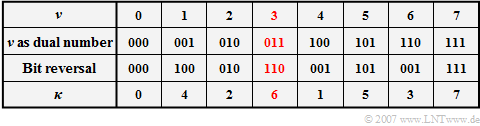
$\text{Example 4: "Bit-reversal" operation}$ 

Radix-2-Algorithm $($"Bit-reversal"  operation for  $N = 8)$

• The new index  $\kappa$  is obtained by writing the index  $\nu$  as a dual number and then representing the  $\text{log}_2 \hspace{0.05cm} N$  bits in reverse order.
• For example,  $\nu = 3$  becomes the new index  $\kappa = 6$.

Exercises for the chapter

Exercise 5.5: Fast Fourier Transform

Exercise 5.5Z: Complexity of the FFT