Difference between revisions of "Theory of Stochastic Signals/Exponentially Distributed Random Variables"
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Continuous Random Variables |
| − | |Vorherige Seite= | + | |Vorherige Seite= Gaussian Distributed Random Variables |
| − | |Nächste Seite= | + | |Nächste Seite=Further Distributions |
}} | }} | ||
==One-sided exponential distribution== | ==One-sided exponential distribution== | ||
| Line 9: | Line 9: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | + | A continuous random variable $x$ is called (one-sided) '''exponentially distributed''' if it can take only non–negative values and the PDF for $x>0$ has the following shape: | |
:$$f_x(x)=\it \lambda\cdot\rm e^{\it -\lambda \hspace{0.05cm}\cdot \hspace{0.03cm} x}.$$}} | :$$f_x(x)=\it \lambda\cdot\rm e^{\it -\lambda \hspace{0.05cm}\cdot \hspace{0.03cm} x}.$$}} | ||
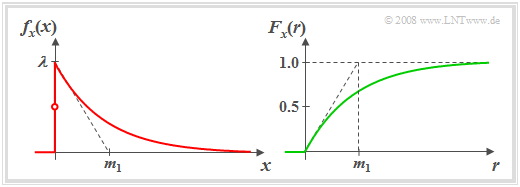
| − | [[File: P_ID72__Sto_T_3_6_S1_neu.png | + | [[File: P_ID72__Sto_T_3_6_S1_neu.png |right|frame| PDF and CDF of an exponentially distributed random variable]] |
| − | + | The left image shows the ''probability density function'' (PDF) of such an exponentially distributed random variable $x$. Highlight: | |
| − | * | + | *The larger the distribution parameter $λ$ is, the steeper the decay occurs. |
| − | * | + | *By definition $f_{x}(0) = λ/2$, i.e. the mean of left-hand limit $(0)$ and right-hand limit $(\lambda)$. |
| − | + | For the ''cumulative distribution function'' (right graph), we obtain for $r > 0$ by integration over the PDF: | |
:$$F_{x}(r)=1-\rm e^{\it -\lambda\hspace{0.05cm}\cdot \hspace{0.03cm} r}.$$ | :$$F_{x}(r)=1-\rm e^{\it -\lambda\hspace{0.05cm}\cdot \hspace{0.03cm} r}.$$ | ||
| − | + | The ''moments'' of the one-sided exponential distribution are generally equal to | |
:$$m_k = k!/λ^k.$$ | :$$m_k = k!/λ^k.$$ | ||
| − | + | From this and from Steiner's theorem, we get for the mean and the dispersion: | |
:$$m_1={1}/{\lambda},$$ | :$$m_1={1}/{\lambda},$$ | ||
:$$\sigma=\sqrt{m_2-m_1^2}=\sqrt{\frac{2}{\lambda^2}-\frac{1}{\lambda^2}}={1}/{\lambda}.$$ | :$$\sigma=\sqrt{m_2-m_1^2}=\sqrt{\frac{2}{\lambda^2}-\frac{1}{\lambda^2}}={1}/{\lambda}.$$ | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 1:}$ The exponential distribution has great importance for reliability studies, and the term "lifetime distribution" is also commonly used in this context. |
| − | * | + | *In these applications, the random variable is often the time $t$ that elapses before a component fails. |
| − | * | + | *Furthermore, it should be noted that the exponential distribution is closely related to the [[Theory_of_Stochastic_Signals/Poisson_Distribution|Poisson distribution]] . }} |
==Transformation of random variables== | ==Transformation of random variables== | ||
<br> | <br> | ||
| − | + | To generate such an exponentially distributed random variable on a digital computer, for example, a '''nonlinear transformation''' The underlying principle is first stated here in general terms. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Procedure:}$ If a continuous random variable $u$ possesses the PDF $f_{u}(u)$, then the probability density function of the random variable transformed at the nonlinear characteristic $x = g(u)$ $x$ holds: |
:$$f_{x}(x)=\frac{f_u(u)}{\mid g\hspace{0.05cm}'(u)\mid}\Bigg \vert_{\hspace{0.1cm} u=h(x)}.$$ | :$$f_{x}(x)=\frac{f_u(u)}{\mid g\hspace{0.05cm}'(u)\mid}\Bigg \vert_{\hspace{0.1cm} u=h(x)}.$$ | ||
| − | + | Here $g\hspace{0.05cm}'(u)$ denotes the derivative of the characteristic curve $g(u)$ and $h(x)$ gives the inverse function to $g(u)$ . }} | |
| − | * | + | *The above equation is valid, however, only under the condition that the derivative $g\hspace{0.03cm}'(u) \ne 0$ . |
| − | * | + | *For a characteristic with horizontal sections $(g\hspace{0.05cm}'(u) = 0)$ additional Dirac functions appear in the PDF if the input quantity has components in the range. |
| − | * | + | *The weights of these Dirac functions are equal to the probabilities that the input quantity lies in these domains. |
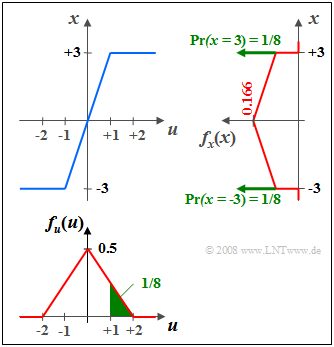
| − | [[File:P_ID76__Sto_T_3_6_S2_neu.png |frame| | + | [[File:P_ID76__Sto_T_3_6_S2_neu.png |frame| To transform random variables | right]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 2:}$ |
| − | + | Given a random variable distributed between $-2$ and $+2$ triangularly $u$ on a nonlinearity with characteristic $x = g(u)$, | |
| − | * | + | *which, in the range $\vert u \vert ≤ 1$ triples the input values, and |
| − | * | + | *mapping all values $\vert u \vert > 1$ to $x = \pm 3$ depending on the sign, |
| − | + | then the PDF $f_{x}(x)$ sketched on the right is obtained. | |
| − | + | Please note: | |
| − | '''(1)''' | + | '''(1)''' Due to the amplification by a factor of $3$ $f_{x}(x)$ is wider and lower than $f_{u}(u) by this factor.$ |
| − | '''(2)''' | + | '''(2)''' The two horizontal limits of the characteristic at $u = ±1$ lead to the two Dirac functions at $x = ±3$, each with weight $1/8$. |
| − | '''(3)''' | + | '''(3)''' The weight $1/8$ corresponds to the green areas in the PDF $f_{u}(u).$}} |
==Erzeugung einer exponentialverteilten Zufallsgröße== | ==Erzeugung einer exponentialverteilten Zufallsgröße== | ||
| Line 76: | Line 76: | ||
:$$x=g_1(u) =\frac{1}{\lambda}\cdot \rm ln \ (\frac{1}{1-\it u}).$$ | :$$x=g_1(u) =\frac{1}{\lambda}\cdot \rm ln \ (\frac{1}{1-\it u}).$$ | ||
| − | Es kann gezeigt werden, dass durch diese Kennlinie $x=g_1(u)$ eine einseitig exponentialverteilte Zufallsgröße $x$ mit folgender | + | Es kann gezeigt werden, dass durch diese Kennlinie $x=g_1(u)$ eine einseitig exponentialverteilte Zufallsgröße $x$ mit folgender PDF entsteht <br>(Herleitung siehe [[Theory_of_Stochastic_Signals/Exponentialverteilte_Zufallsgrößen#Herleitung_der_zugeh.C3.B6rigen_Transformationskennlinie|nächste Seite]]): |
:$$f_{x}(x)=\lambda\cdot\rm e^{\it -\lambda \hspace{0.05cm}\cdot \hspace{0.03cm} x}\hspace{0.2cm}{\rm f\ddot{u}r}\hspace{0.2cm} {\it x}>0.$$ | :$$f_{x}(x)=\lambda\cdot\rm e^{\it -\lambda \hspace{0.05cm}\cdot \hspace{0.03cm} x}\hspace{0.2cm}{\rm f\ddot{u}r}\hspace{0.2cm} {\it x}>0.$$ | ||
| − | *Für $x = 0$ ist der | + | *Für $x = 0$ ist der PDF-Wert nur halb so groß $(\lambda/2)$. |
* Negative $x$-Werte treten nicht auf, da für $0 ≤ u < 1$ das Argument der (natürlichen) Logarithmus–Funktion nicht kleiner wird als $1$.}} | * Negative $x$-Werte treten nicht auf, da für $0 ≤ u < 1$ das Argument der (natürlichen) Logarithmus–Funktion nicht kleiner wird als $1$.}} | ||
| − | Die gleiche | + | Die gleiche PDF erhält man übrigens mit der monoton fallenden Kennlinie |
:$$x=g_2(u)=\frac{1}{\lambda}\cdot \rm ln \ (\frac{1}{\it u})=-\frac{1}{\lambda}\cdot \rm ln(\it u \rm ).$$ | :$$x=g_2(u)=\frac{1}{\lambda}\cdot \rm ln \ (\frac{1}{\it u})=-\frac{1}{\lambda}\cdot \rm ln(\it u \rm ).$$ | ||
| Line 96: | Line 96: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Aufgabenstellung:}$ | $\text{Aufgabenstellung:}$ | ||
| − | Nun wird die bereits auf der letzten Seite verwendete Transformationskennlinie $x = g_1(u)= g(u)$ hergeleitet, die aus einer zwischen $0$ und $1$ gleichverteilten Zufallsgröße $u$ mit der Wahrscheinlichkeitsdichtefunktion ( | + | Nun wird die bereits auf der letzten Seite verwendete Transformationskennlinie $x = g_1(u)= g(u)$ hergeleitet, die aus einer zwischen $0$ und $1$ gleichverteilten Zufallsgröße $u$ mit der Wahrscheinlichkeitsdichtefunktion (PDF) $f_{u}(u)$ eine einseitig exponentialverteilte Zufallsgröße $x$ mit der PDF $f_{x}(x)$ formt: |
:$$f_{u}(u)= \left\{ \begin{array}{*{2}{c} } 1 & \rm falls\hspace{0.3cm} 0 < {\it u} < 1,\\ 0.5 & \rm falls\hspace{0.3cm} {\it u} = 0, {\it u} = 1,\\ 0 & \rm sonst, \\ \end{array} \right. \hspace{0.5cm}\Rightarrow \hspace{0.5cm} | :$$f_{u}(u)= \left\{ \begin{array}{*{2}{c} } 1 & \rm falls\hspace{0.3cm} 0 < {\it u} < 1,\\ 0.5 & \rm falls\hspace{0.3cm} {\it u} = 0, {\it u} = 1,\\ 0 & \rm sonst, \\ \end{array} \right. \hspace{0.5cm}\Rightarrow \hspace{0.5cm} | ||
| Line 107: | Line 107: | ||
'''(1)''' Ausgehend von der allgemeinen Transformationsgleichung | '''(1)''' Ausgehend von der allgemeinen Transformationsgleichung | ||
:$$f_{x}(x)=\frac{f_{u}(u)}{\mid g\hspace{0.05cm}'(u) \mid }\Bigg \vert _{\hspace{0.1cm} u=h(x)}$$ | :$$f_{x}(x)=\frac{f_{u}(u)}{\mid g\hspace{0.05cm}'(u) \mid }\Bigg \vert _{\hspace{0.1cm} u=h(x)}$$ | ||
| − | erhält man durch Umstellen und Einsetzen der vorgegebenen | + | erhält man durch Umstellen und Einsetzen der vorgegebenen PDF $f_{ x}(x):$ |
:$$\mid g\hspace{0.05cm}'(u)\mid\hspace{0.1cm}=\frac{f_{u}(u)}{f_{x}(x)}\Bigg \vert _{\hspace{0.1cm} x=g(u)}= {1}/{\lambda} \cdot {\rm e}^{\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}g(u)}.$$ | :$$\mid g\hspace{0.05cm}'(u)\mid\hspace{0.1cm}=\frac{f_{u}(u)}{f_{x}(x)}\Bigg \vert _{\hspace{0.1cm} x=g(u)}= {1}/{\lambda} \cdot {\rm e}^{\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}g(u)}.$$ | ||
Hierbei gibt $x = g\hspace{0.05cm}'(u)$ die Ableitung der Kennlinie an, die wir als monoton steigend voraussetzen. | Hierbei gibt $x = g\hspace{0.05cm}'(u)$ die Ableitung der Kennlinie an, die wir als monoton steigend voraussetzen. | ||
Revision as of 23:53, 3 January 2022
Contents
One-sided exponential distribution
$\text{Definition:}$ A continuous random variable $x$ is called (one-sided) exponentially distributed if it can take only non–negative values and the PDF for $x>0$ has the following shape:
- $$f_x(x)=\it \lambda\cdot\rm e^{\it -\lambda \hspace{0.05cm}\cdot \hspace{0.03cm} x}.$$
The left image shows the probability density function (PDF) of such an exponentially distributed random variable $x$. Highlight:
- The larger the distribution parameter $λ$ is, the steeper the decay occurs.
- By definition $f_{x}(0) = λ/2$, i.e. the mean of left-hand limit $(0)$ and right-hand limit $(\lambda)$.
For the cumulative distribution function (right graph), we obtain for $r > 0$ by integration over the PDF:
- $$F_{x}(r)=1-\rm e^{\it -\lambda\hspace{0.05cm}\cdot \hspace{0.03cm} r}.$$
The moments of the one-sided exponential distribution are generally equal to
- $$m_k = k!/λ^k.$$
From this and from Steiner's theorem, we get for the mean and the dispersion:
- $$m_1={1}/{\lambda},$$
- $$\sigma=\sqrt{m_2-m_1^2}=\sqrt{\frac{2}{\lambda^2}-\frac{1}{\lambda^2}}={1}/{\lambda}.$$
$\text{Example 1:}$ The exponential distribution has great importance for reliability studies, and the term "lifetime distribution" is also commonly used in this context.
- In these applications, the random variable is often the time $t$ that elapses before a component fails.
- Furthermore, it should be noted that the exponential distribution is closely related to the Poisson distribution .
Transformation of random variables
To generate such an exponentially distributed random variable on a digital computer, for example, a nonlinear transformation The underlying principle is first stated here in general terms.
$\text{Procedure:}$ If a continuous random variable $u$ possesses the PDF $f_{u}(u)$, then the probability density function of the random variable transformed at the nonlinear characteristic $x = g(u)$ $x$ holds:
- $$f_{x}(x)=\frac{f_u(u)}{\mid g\hspace{0.05cm}'(u)\mid}\Bigg \vert_{\hspace{0.1cm} u=h(x)}.$$
Here $g\hspace{0.05cm}'(u)$ denotes the derivative of the characteristic curve $g(u)$ and $h(x)$ gives the inverse function to $g(u)$ .
- The above equation is valid, however, only under the condition that the derivative $g\hspace{0.03cm}'(u) \ne 0$ .
- For a characteristic with horizontal sections $(g\hspace{0.05cm}'(u) = 0)$ additional Dirac functions appear in the PDF if the input quantity has components in the range.
- The weights of these Dirac functions are equal to the probabilities that the input quantity lies in these domains.
$\text{Example 2:}$ Given a random variable distributed between $-2$ and $+2$ triangularly $u$ on a nonlinearity with characteristic $x = g(u)$,
- which, in the range $\vert u \vert ≤ 1$ triples the input values, and
- mapping all values $\vert u \vert > 1$ to $x = \pm 3$ depending on the sign,
then the PDF $f_{x}(x)$ sketched on the right is obtained.
Please note:
(1) Due to the amplification by a factor of $3$ $f_{x}(x)$ is wider and lower than $f_{u}(u) by this factor.$
(2) The two horizontal limits of the characteristic at $u = ±1$ lead to the two Dirac functions at $x = ±3$, each with weight $1/8$.
(3) The weight $1/8$ corresponds to the green areas in the PDF $f_{u}(u).$
Erzeugung einer exponentialverteilten Zufallsgröße
$\text{Vorgehensweise:}$ Nun wird vorausgesetzt, dass die zu transformierende Zufallsgröße $u$ gleichverteilt zwischen $0$ (inklusive) und $1$ (exklusive) ist. Außerdem betrachten wir die monoton steigende Kennlinie
- $$x=g_1(u) =\frac{1}{\lambda}\cdot \rm ln \ (\frac{1}{1-\it u}).$$
Es kann gezeigt werden, dass durch diese Kennlinie $x=g_1(u)$ eine einseitig exponentialverteilte Zufallsgröße $x$ mit folgender PDF entsteht
(Herleitung siehe nächste Seite):
- $$f_{x}(x)=\lambda\cdot\rm e^{\it -\lambda \hspace{0.05cm}\cdot \hspace{0.03cm} x}\hspace{0.2cm}{\rm f\ddot{u}r}\hspace{0.2cm} {\it x}>0.$$
- Für $x = 0$ ist der PDF-Wert nur halb so groß $(\lambda/2)$.
- Negative $x$-Werte treten nicht auf, da für $0 ≤ u < 1$ das Argument der (natürlichen) Logarithmus–Funktion nicht kleiner wird als $1$.
Die gleiche PDF erhält man übrigens mit der monoton fallenden Kennlinie
- $$x=g_2(u)=\frac{1}{\lambda}\cdot \rm ln \ (\frac{1}{\it u})=-\frac{1}{\lambda}\cdot \rm ln(\it u \rm ).$$
Bitte beachten Sie:
- Bei einer Rechnerimplementierung entsprechend der ersten Transformationskennlinie $x=g_1(u)$ ist der Wert $u = 1$ auszuschließen.
- Verwendet man die zweite Transformationskennlinie $x=g_2(u)$, so muss dagegen der Wert $u =0$ ausgeschlossen werden.
Das Lernvideo Erzeugung einer Exponentialverteilung soll die hier abgeleiteten Transformationen verdeutlichen.
Herleitung der zugehörigen Transformationskennlinie
$\text{Aufgabenstellung:}$ Nun wird die bereits auf der letzten Seite verwendete Transformationskennlinie $x = g_1(u)= g(u)$ hergeleitet, die aus einer zwischen $0$ und $1$ gleichverteilten Zufallsgröße $u$ mit der Wahrscheinlichkeitsdichtefunktion (PDF) $f_{u}(u)$ eine einseitig exponentialverteilte Zufallsgröße $x$ mit der PDF $f_{x}(x)$ formt:
- $$f_{u}(u)= \left\{ \begin{array}{*{2}{c} } 1 & \rm falls\hspace{0.3cm} 0 < {\it u} < 1,\\ 0.5 & \rm falls\hspace{0.3cm} {\it u} = 0, {\it u} = 1,\\ 0 & \rm sonst, \\ \end{array} \right. \hspace{0.5cm}\Rightarrow \hspace{0.5cm} f_{x}(x)= \left\{ \begin{array}{*{2}{c} } \lambda\cdot\rm e^{\it -\lambda\hspace{0.03cm} \cdot \hspace{0.03cm} x} & \rm falls\hspace{0.3cm} {\it x} > 0,\\ \lambda/2 & \rm falls\hspace{0.3cm} {\it x} = 0 ,\\ 0 & \rm falls\hspace{0.3cm} {\it x} < 0. \\ \end{array} \right.$$
$\text{Problemlösung:}$
(1) Ausgehend von der allgemeinen Transformationsgleichung
- $$f_{x}(x)=\frac{f_{u}(u)}{\mid g\hspace{0.05cm}'(u) \mid }\Bigg \vert _{\hspace{0.1cm} u=h(x)}$$
erhält man durch Umstellen und Einsetzen der vorgegebenen PDF $f_{ x}(x):$
- $$\mid g\hspace{0.05cm}'(u)\mid\hspace{0.1cm}=\frac{f_{u}(u)}{f_{x}(x)}\Bigg \vert _{\hspace{0.1cm} x=g(u)}= {1}/{\lambda} \cdot {\rm e}^{\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}g(u)}.$$
Hierbei gibt $x = g\hspace{0.05cm}'(u)$ die Ableitung der Kennlinie an, die wir als monoton steigend voraussetzen.
(2) Mit dieser Annahme erhält man $\vert g\hspace{0.05cm}'(u)\vert = g\hspace{0.05cm}'(u) = {\rm d}x/{\rm d}u$ und die Differentialgleichung ${\rm d}u = \lambda\ \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm} x}\, {\rm d}x$ mit der Lösung $u = K - {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm} x}.$
(3) Aus der Bedingung, dass die Eingangsgröße $u =0$ zum Ausgangswert $x =0$ führen soll, erhält man für die Konstante $K =1$ und damit $u = 1- {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm} x}.$
(4) Löst man diese Gleichung nach $x$ auf, so ergibt sich die vorne angegebene Gleichung:
- $$x = g_1(u)= \frac{1}{\lambda} \cdot {\rm ln} \left(\frac{1}{1 - u} \right) .$$
- Bei einer Rechnerimplementierung ist allerdings sicherzustellen, dass für die gleichverteilte Eingangsgröße $u$ der kritische Wert $1$ ausgeschlossen wird.
- Dies wirkt sich jedoch auf das Endergebnis (fast) nicht aus.
Two-sided exponential distribution - Laplace distribution
In engem Zusammenhang mit der Exponentialverteilung steht die sogenannte Laplaceverteilung mit der Wahrscheinlichkeitsdichtefunktion
- $$f_{x}(x)=\frac{\lambda}{2}\cdot\rm e^{\it -\lambda \hspace{0.05cm} \cdot \hspace{0.05cm} | x|}.$$
Die Laplaceverteilung ist eine zweiseitige Exponentialverteilung, die insbesondere die Amplitudenverteilung von Sprach– und Musiksignalen ausreichend gut approximiert.
- Die Momente $k$–ter Ordnung ⇒ $m_k$ der Laplaceverteilung stimmen für geradzahliges $k$ mit denen der Exponentialverteilung überein.
- Für ungeradzahliges $k$ ergibt sich bei der (symmetrischen) Laplaceverteilung dagegen stets $m_k= 0$.
Zur Generierung verwendet man eine zwischen $±1$ gleichverteilte Zufallsgröße $v$ (wobei $v = 0$ ausgeschlossen werden muss) und die Transformationskennlinie
- $$x=\frac{{\rm sign}(v)}{\lambda}\cdot \rm ln(\it v \rm ).$$
Weitere Hinweise:
- Aus der Aufgabe 3.8 erkennt man weitere Eigenschaften der Laplaceverteilung.
- Im Lernvideo Wahrscheinlichkeit und WDF wird gezeigt, welche Bedeutung die Laplaceverteilung für die Beschreibung von Sprach– und Musiksignalen hat.
- Mit dem Applet WDF, VTF und Momente können Sie sich die Kenngrößen $($WDF, VTF, Momente$)$ von Exponential- und Laplaceverteilung anzeigen lassen.
- Wir weisen Sie auch auf das Applet Zweidimensionale Laplace-Zufallsgrößen hin.
Aufgaben zum Kapitel
Aufgabe 3.8: Verstärkung und Begrenzung
Aufgabe 3.8Z: Kreis(ring)fläche
Aufgabe 3.9: Kennlinie für Cosinus-WDF
Aufgabe 3.9Z: Sinustransformation