Further Distributions

Rayleigh PDF

$\text{Definition:}$ A continuous random variable $x$ is called Rayleigh distributed if it cannot take negative values and the probability density function (PDF) for $x \ge 0$ with the distribution parameter $λ$ has the following shape:

$$f_{x}(x)=\frac{x}{\lambda^2}\cdot {\rm e}^{-x^2 / ( 2 \hspace{0.05cm}\cdot \hspace{0.05cm}\lambda^2) } .$$

The name goes back to the English physicist John William Strutt the "third Baron Rayleigh". In 1904 he received the physics–Nobel Prize.

The Rayleigh distribution plays a central role in the description of time-varying channels. Such channels are described in the book Mobile Communications .
For example, non-frequency selective fading exhibits such a distribution when there is no line-of-sight between the base station and the mobile user.

Characteristic properties of Rayleigh distribution:

A Rayleigh distributed random variable $x$ cannot take negative values.
The theoretically possible value $x = 0$ also occurs only with probability "zero".
The $k$-th moment of a Rayleigh distributed random variable $x$ results in general to

$$m_k=(2\cdot \lambda^{\rm 2})^{\it k/\rm 2}\cdot {\rm \Gamma}( 1+ {\it k}/{\rm 2}) \hspace{0.3cm}{\rm with }\hspace{0.3cm}{\rm \Gamma}(x)= \int_{0}^{\infty} t^{x-1} \cdot {\rm e}^{-t} \hspace{0.1cm}{\rm d}t.$$

From this, the mean $m_1$ and the rms $\sigma_1$ can be calculated as follows:

$$m_1=\sqrt{2}\cdot \lambda\cdot {\rm \Gamma}(1.5) = \sqrt{2}\cdot \lambda\cdot {\sqrt{\pi}}/{2} =\lambda\cdot\sqrt{{\pi}/{2}},$$

$$m_2=2 \lambda^2 \cdot {\rm \Gamma}(2) = 2 \lambda^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\sigma = \sqrt{m_2 - m_1^2} =\lambda\cdot\sqrt{2-{\pi}/{2}}.$$

To model a Rayleigh distributed random variable $x$ one uses, for example, two Gaussian distributed, mean-free, and statistically independent random variables $u$ and $v$, both of which have rms $σ = λ$ The variables $u$ and $v$ are then linked as follows:

$$x=\sqrt{u^2+v^2}.$$

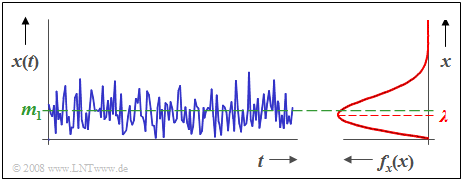
Sample signal and PDF of a Rayleigh distributed random variable

$\text{Example 1:}$ The graph shows:

the time course $x(t)$ of a Rayleigh distributed random variable as well as.
the associated density function $f_{x}(x)$.

One can see from this representation:

The Rayleigh–PDF is always asymmetric.
The mean $m_1$ lies about $25\%$ above the PDF maximum.
The PDF maximum occurs at $x = λ$ .

Rice PDF

Auch die Riceverteilung spielt für die Beschreibung zeitvarianter Kanäle eine wichtige Rolle, unter anderem auch deshalb,

weil nichtfrequenzselektives Fading dann riceverteilt ist,
wenn zwischen der Basisstation und dem Mobilteilnehmer eine Sichtverbindung besteht.

$\text{Definition:}$ Eine kontinuierliche Zufallsgröße $x$ nennt man riceverteilt, wenn sie keine negativen Werte annehmen kann und die Wahrscheinlichkeitsdichtefunktion (WDF) für $x > 0$ den folgenden Verlauf hat:

$$f_{\rm x}(x)=\frac{x}{\lambda^2}\cdot{\rm e}^{-({C^2+\it x^{\rm 2} })/ ({\rm 2 \it \lambda^{\rm 2} })}\cdot {\rm I_0}(\frac{\it x\cdot C}{\lambda^{\rm 2} }) \hspace{0.4cm}{\rm mit} \hspace{0.4cm} {\rm I_0}(x) = \sum_{k=0}^{\infty}\frac{(x/2)^{2k} }{k! \cdot {\rm \Gamma ({\it k}+1)} }.$$

${\rm I_0}( ... )$ bezeichnet die modifizierte Besselfunktion nullter Ordnung.

Der Name geht auf den Mathematiker und Logiker Henry Gordon Rice zurück. Er lehrte als Mathematikprofessor an der University of New Hampshire.

Charakteristische Eigenschaften der Riceverteilung:

Der gegenüber der Rayleighverteilung zusätzliche Parameter $C$ ist ein Maß für die „Stärke” der Direktkomponente. Je größer der Quotient $C/λ$ ist, desto mehr nähert sich der Rice–Kanal dem Gauß–Kanal an. Für $C = 0$ geht die Riceverteilung in die Rayleighverteilung über.
Bei der Riceverteilung ist der Ausdruck für das Moment $m_k$ deutlich komplizierter und nur mit Hilfe hypergeometrischer Funktionen angebbar. Ist jedoch $λ$ sehr viel kleiner als $C$, so gilt $m_1 ≈ C$ und $σ ≈ λ$.
Unter diesen Voraussetzungen kann die Riceverteilung durch eine Gaußverteilung mit Mittelwert $C$ und Streuung $λ$ angenähert werden.
Zur Modellierung einer riceverteilten Zufallsgröße $x$ verwenden wir ein ähnliches Modell wie für die Rayleighverteilung, nur muss nun zumindest eine der beiden gaußverteilten und statistisch voneinander unabhängigen Zufallsgrößen $(u$ und/oder $v$ ) einen Mittelwert ungleich Null aufweisen.

$$x=\sqrt{u^2+v^2}\hspace{0.5cm}{\rm mit}\hspace{0.5cm}|m_u| + |m_v| > 0 .$$

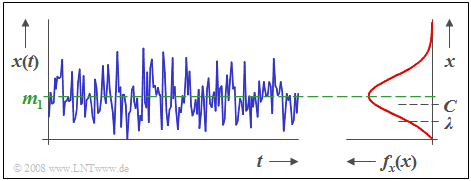
Mustersignal und WDF einer riceverteilten Zufallsgröße

$\text{Beispiel 2:}$ Die Grafik zeigt den zeitlichen Verlauf einer riceverteilten Zufallsgröße $x$ sowie deren Dichtefunktion $f_{\rm x}(x)$, wobei $C/λ = 2$ gilt.

Etwas salopp ausgedrückt: Die Riceverteilung ist ein Kompromiss zwischen der Rayleigh– und der Gaußverteilung.
Der Mittelwert $m_1$ ist hier etwas größer als $C$.

Mit dem interaktiven Applet WDF, VTF und Momente spezieller Verteilungen können Sie sich unter anderem die Kenngrößen $($WDF, VTF, Momente$)$ der Rayleigh– sowie der Riceverteilung anzeigen lassen.

Cauchy PDF

$\text{Definition:}$ Eine kontinuierliche Zufallsgröße $x$ nennt man cauchyverteilt, wenn die Wahrscheinlichkeitsdichtefunktion (WDF) und die Verteilungsfunktion (VTF) mit dem Verteilungsparameter $λ$ folgende Form haben:

$$f_{x}(x)=\frac{1}{\pi}\cdot\frac{\lambda}{\lambda^2+x^2},$$

$$F_{x}(r)={\rm 1}/{2}+{\rm arctan}({r}/{\lambda}).$$

Manchmal wird in der Literatur auch noch ein Mittelwert $m_1$ berücksichtigt.

Der Name geht auf den französischen Mathematiker Augustin-Louis Cauchy zurück, ein Pionier der Analysis, der die von Gottfried Wilhelm Leibniz und Sir Isaac Newton aufgestellten Grundlagen weiterentwickelte und fundamentale Aussagen formal bewies. Insbesondere stammen viele zentrale Sätze der Funktionentheorie von Cauchy.

Die Cauchyverteilung hat weniger praktische Bedeutung für die Nachrichtentechnik, ist mathematisch aber sehr interessant.

Sie weist in der symmetrischen Form $($mit Mittelwert $m_1 = 0)$ folgende Eigenschaften auf:

Bei der Cauchyverteilung besitzen alle Momente $m_k$ für gerades $k$ einen unendlich großen Wert, und zwar unabhängig vom Parameter $λ$.

Damit besitzt diese Verteilung auch eine unendlich große Varianz $\sigma^2 = m_2$ ⇒ Leistung.
Deshalb ist es offensichtlich, dass keine physikalische Größe cauchyverteilt sein kann.
Der Quotient $u/v$ zweier unabhängiger gaußverteilter mittelwertfreier Größen $u$ und $v$ ist mit dem Verteilungsparameter $λ = σ_u/σ_v$ cauchyverteilt.
Eine cauchyverteilte Zufallsgröße $x$ kann aus einer zwischen $\pm1$ gleichverteilten Größe $u$ durch folgende nichtlineare Transformation erzeugt werden:

$$x=\lambda \cdot {\tan}( {\pi}/{2}\cdot u).$$

Aufgrund der Symmetrie sind für ungerades $k$ alle Momente $m_k = 0$, wenn man vom "Cauchy Principal Value" ausgeht.
Somit gilt auch für den Mittelwert $m_X = 0$ und die Charliersche Schiefe $S_X = 0$.

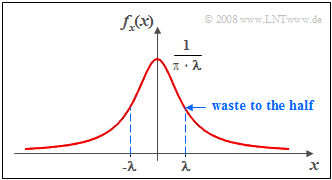
WDF einer cauchyverteilten Zufallsgröße

$\text{Beispiel 3:}$ Die Grafik zeigt den typischen Verlauf der Cauchy-WDF.

Zu erkennen ist der langsame Abfall dieser Funktion zu den Rändern hin.
Da dieser asymptotisch mit $1/x^2$ erfolgt, sind die Varianz und alle Momente höherer Ordnung (mit geradzahligem Index) unendlich groß.

Tschebyscheffsche Ungleichung

Bei einer Zufallsgröße $x$ mit bekannter Wahrscheinlichkeitsdichtefunktion $f_{x}(x)$ kann die Wahrscheinlichkeit, dass die Zufallsgröße $x$ betragsmäßig um mehr als einen Wert $ε$ von ihrem Mittelwert $m_{x}$ abweicht, entsprechend der in diesem Kapitel allgemein beschriebenen Weise exakt berechnet werden.

rechts

Ist neben dem Mittelwert $m_{x}$ zwar noch die Streuung $σ_{x}$ bekannt, nicht jedoch der exakte WDF-Verlauf $f_{x}(x)$, so lässt sich für diese Wahrscheinlichkeit zumindest eine obere Schranke angeben:

$${\rm Pr}(|x - m_{\rm x}|\ge\varepsilon)\le\frac{\sigma_{x}^{\rm 2}}{\varepsilon^{\rm 2}}. $$

Diese von Pafnuti L. Tschebyscheff angegebene Schranke – bekannt als „Tschebyscheffsche Ungleichung” – ist im Allgemeinen allerdings nur eine sehr grobe Näherung für die tatsächliche Überschreitungswahrscheinlichkeit. Sie sollte deshalb nur bei unbekanntem Verlauf der WDF $f_{x}(x)$ angewendet werden.

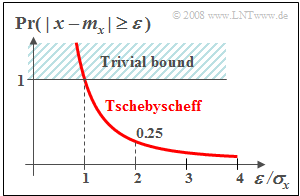
$\text{Beispiel 4:}$ Wir gehen von einer gaußverteilten und mittelwertfreien Zufallsgröße $x$ aus.

Damit ist die Wahrscheinlichkeit, dass deren Betrag $\vert x \vert $ größer als die dreifache Streuung $(3 · σ_{x})$ ist, einfach berechenbar. Ergebnis: ${\rm 2 · Q(3) ≈ 2.7 · 10^{-3} }.$
Die Tschebyscheffsche Ungleichung liefert hier als eine obere Schranke den deutlich zu großen Wert $1/9 ≈ 0.111$.
Diese Schranke nach Tschebyscheff würde für jede beliebige WDF–Form ebenfalls gelten.

Aufgaben zum Kapitel

Aufgabe 3.10: Rayleighfading

Aufgabe 3.10Z: Rayleigh? Oder Rice?

Aufgabe 3.11: Tschebyscheffsche Ungleichung

Aufgabe 3.12: Cauchyverteilung