Contents
Rayleigh PDF
$\text{Definition:}$ A continuous-valued random variable $x$ is called »Rayleigh distributed« if it cannot take negative values and the probability density function $\rm (PDF)$ for $x \ge 0$ has the following shape with the distribution parameter $λ$:
- $$f_{x}(x)=\frac{x}{\lambda^2}\cdot {\rm e}^{-x^2 / ( 2 \hspace{0.05cm}\cdot \hspace{0.05cm}\lambda^2) } .$$
The name goes back to the English physicist $\text{John William Strutt}$ the "third Baron Rayleigh". In 1904 he received the Physics Nobel Prize.
- The Rayleigh distribution plays a central role in the description of time-varying channels. Such channels are described in the book "Mobile Communications".
- For example, "non-frequency selective fading" exhibits such a distribution when there is no "line-of-sight" between the base station and the mobile user.
Characteristic properties of Rayleigh distribution:
- A Rayleigh distributed random variable $x$ cannot take negative values.
- The theoretically possible value $x = 0$ also occurs only with probability "zero".
- The $k$-th moment of a Rayleigh distributed random variable $x$ results in general to
- $$m_k=(2\cdot \lambda^{\rm 2})^{\it k/\rm 2}\cdot {\rm \Gamma}( 1+ {\it k}/{\rm 2}) \hspace{0.3cm}{\rm with }\hspace{0.3cm}{\rm \Gamma}(x)= \int_{0}^{\infty} t^{x-1} \cdot {\rm e}^{-t} \hspace{0.1cm}{\rm d}t.$$
- From this, the mean $m_1$ and the standard deviation $\sigma$ can be calculated as follows:
- $$m_1=\sqrt{2}\cdot \lambda\cdot {\rm \Gamma}(1.5) = \sqrt{2}\cdot \lambda\cdot {\sqrt{\pi}}/{2} =\lambda\cdot\sqrt{{\pi}/{2}},$$
- $$m_2=2 \lambda^2 \cdot {\rm \Gamma}(2) = 2 \lambda^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\sigma = \sqrt{m_2 - m_1^2} =\lambda\cdot\sqrt{2-{\pi}/{2}}.$$
- To model a Rayleigh distributed random variable $x$ one uses, for example, two Gaussian distributed zero mean and statistically independent random variables $u$ and $v$, both of which have rms $σ = λ$. The variables $u$ and $v$ are then linked as follows:
- $$x=\sqrt{u^2+v^2}.$$
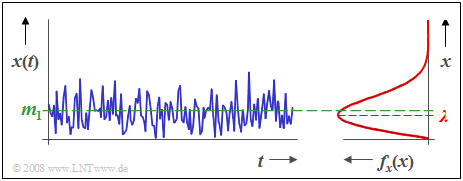
$\text{Example 1:}$ The graph shows:
- the time course $x(t)$ of a Rayleigh distributed random variable, as well as,
- the associated probability density function $f_{x}(x)$.
One can see from this representation:
- The Rayleigh PDF is always asymmetric.
- The mean $m_1$ lies about $25\%$ above the PDF maximum.
- The PDF maximum occurs at $x = λ$.
With the HTML 5/JavaScript applet "PDF, CDF and Moments of Special Distributions" you can display, among others, the characteristics of the Rayleigh distribution.
Rice PDF
Rice distribution also plays an important role in the description of time-varying channels,
- because "non-frequency selective fading" is Rice distributed,
- if there is "line-of-sight" between the base station and the mobile subscriber.
$\text{Definition:}$ A continuous-valued random variable $x$ is called »Rice distributed« if it cannot take negative values and the probability density function $\rm (PDF)$ for $x > 0$ has the following shape:
- $$f_{\rm x}(x)=\frac{x}{\lambda^2}\cdot{\rm e}^{-({C^2+\it x^{\rm 2} })/ ({\rm 2 \it \lambda^{\rm 2} })}\cdot {\rm I_0}(\frac{\it x\cdot C}{\lambda^{\rm 2} }) \hspace{0.4cm}{\rm with} \hspace{0.4cm} {\rm I_0}(x) = \sum_{k=0}^{\infty}\frac{(x/2)^{2k} }{k! \cdot {\rm \gamma ({\it k}+1)} }.$$
${\rm I_0}( ... )$ denotes the $\text{modified zero-order Bessel function}$.
The name is due to the mathematician and logician $\text{Henry Gordon Rice}$. He taught as a mathematics professor at the University of New Hampshire.
Characteristic properties of the Rice distribution:
- The additional parameter $C$ compared to the Rayleigh distribution is a measure of the "strength" of the direct component. The larger the quotient $C/λ$, the more the Rice channel approximates the Gaussian channel. For $C = 0$ the Rice distribution transitions to the $\text{Rayleigh distribution}$.
- In the Rice distribution, the expression for the moment $m_k$ is much more complicated and can only be specified using hypergeometric functions.
- However, if $λ \ll C$, then $m_1 ≈ C$ and $σ ≈ λ$ holds.
- Under these conditions, the Rice distribution can be approximated by a $\text{Gaussian distribution}$ with mean $C$ and rms $λ$.
- To model a Rice distributed random variable $x$ we use a similar model as for the Rayleigh distribution, except that now at least one of the two Gaussian distributed and statistically independent random variables $(u$ and/or $v$ ) must have a non-zero mean.
- $$x=\sqrt{u^2+v^2}\hspace{0.5cm}{\rm with}\hspace{0.5cm}|m_u| + |m_v| > 0 .$$
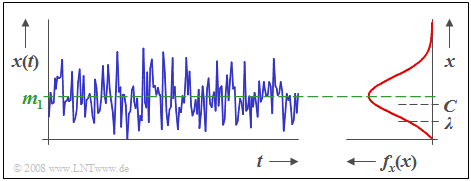
$\text{Example 2:}$ The graph shows the time course of a Rice distributed random variable $x$ and its probability density function $f_{\rm x}(x)$, where $C/λ = 2$ holds.
- Somewhat casually put: The Rice distribution is a compromise between the Rayleigh and the Gaussian distributions.
- Here the mean $m_1$ is slightly larger than $C$.
With the HTML 5/JavaScript applet "PDF, CDF and Moments of Special Distributions" you can display, among others, the characteristics of the Rice distribution.
Cauchy PDF
$\text{Definition:}$ A continuous-valued random variable $x$ is called »Cauchy distributed« if the probability density function $\rm (PDF)$ and the cumulative distribution function $\rm (CDF)$ with parameter $λ$ have the following form:
- $$f_{x}(x)=\frac{1}{\pi}\cdot\frac{\lambda}{\lambda^2+x^2},$$
- $$F_{x}(r)={\rm 1}/{2}+{\rm arctan}({r}/{\lambda}).$$
Sometimes in the literature, a mean $m_1$ is also considered.
The name derives from the French mathematician $\text{Augustin-Louis Cauchy}$, a pioneer of calculus who further developed the foundations established by $\text{Gottfried Wilhelm Leibniz}$ and $\text{Sir Isaac Newton}$ and formally proved fundamental propositions. In particular, many central theorems of "Function Theory" derive from Cauchy.
The Cauchy distribution has less practical significance for communications engineering, but is mathematically very interesting. It has the following properties in the symmetric form $($with mean $m_1 = 0)$:
- For the Cauchy distribution, all moments $m_k$ for even $k$ have an infinitely large value, and this is independent of the parameter $λ$.
- Thus, this distribution also has an infinitely large variance $\sigma^2 = m_2$ ⇒ "power" ⇒ it is obvious that no physical variable can be Cauchy distributed.
- The quotient $u/v$ of two independent Gaussian distributed zero mean variables $u$ and $v$ is Cauchy distributed with the distribution parameter $λ = σ_u/σ_v$ .
- A Cauchy distributed random variable $x$ can be generated from a random variable $\pm1$ uniformly distributed between $u$ by the following $\text{nonlinear transformation}$:
- $$x=\lambda \cdot {\tan}( {\pi}/{2}\cdot u).$$
- Because of symmetry, for odd $k$ all moments $m_k = 0$, assuming the "Cauchy Principal Value".
- So the mean value $m_X = 0$ and the Charlier skewness $S_X = 0$ also hold.
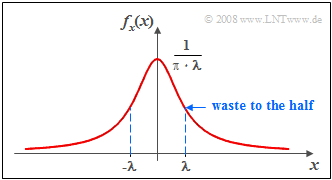
$\text{Example 3:}$ The graph shows the typical course of the Cauchy PDF.
- The slow decline of this function towards the edges can be seen.
- As this occurs asymptotically with $1/x^2$ the variance and all higher order moments (with even index) are infinite.
With the HTML 5/JavaScript applet "PDF, CDF and Moments of Special Distributions" you can display, among others, the characteristics of the Cauchy distribution.
Chebyshev's inequality
Given a random variable $x$ with known probability density function $f_{x}(x)$ the probability that the random variable $x$ deviates in magnitude by more than the value $ε$ from its mean $m_{x}$ can be calculated exactly according to the way generally described in this chapter.
- If besides the mean $m_{x}$ the standard deviation $σ_{x}$ is known, but not the exact $\rm PDF$ course $f_{x}(x)$, at least an upper bound can be given for this probability:
- $${\rm Pr}(|x - m_{\rm x}|\ge\varepsilon)\le\frac{\sigma_{x}^{\rm 2}}{\varepsilon^{\rm 2}}. $$
- This bound given by $\text{Pafnuti L. Chebyshev}$ - known as "Chebyshev's inequality" - is in general only a very rough approximation for the actual exceeding probability. It should therefore be applied only in the case of an unknown course of the PDF $f_{x}(x)$.
$\text{Example 4:}$ We assume a Gaussian distributed and zero mean random variable $x$.
- Thus, the probability that its absolute value $\vert x \vert $ is greater than three times the rms $(3 \cdot σ_{x})$ is easily computable. Result: ${\rm 2 - Q(3) ≈ 2.7 \cdot 10^{-3} }.$
- Chebyshev's inequality yields here as an upper bound the clearly too large value $1/9 ≈ 0.111$.
- This Chebyshev bound would hold for any PDF form.
Exercises for the chapter
Exercise 3.10: Rayleigh Fading
Exercise 3.10Z: Rayleigh? Or Rice?
Exercise 3.11: Chebyshev's Inequality
Exercise 3.12: Cauchy Distribution