Difference between revisions of "Theory of Stochastic Signals/Statistical Dependence and Independence"
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Probability Calculation |
| − | |Vorherige Seite= | + | |Vorherige Seite=Set Theory Basics |
| − | |Nächste Seite= | + | |Nächste Seite=Markov Chains |
}} | }} | ||
| − | == | + | ==General Definition of Statistical Dependence== |
<br> | <br> | ||
| − | + | So far we have not paid much attention to ''statistical dependence'' between events, even though we have already used it as in the case of two disjoint sets: If an element belongs to $A$, it cannot with certainty also be contained in the disjoint set $B$ . | |
| − | + | The strongest form of dependence at all is such a '''deterministic dependence''' between two sets or two events. Less pronounced is the statistical dependence. Let us start with its complement: | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | + | Two events $A$ and $B$ are called '''statistically independent''' , if the probability of the intersection $A ∩ B$ is equal to the product of the individual probabilities: | |
:$${\rm Pr}(A \cap B) = {\rm Pr}(A)\cdot {\rm Pr}(B).$$}} | :$${\rm Pr}(A \cap B) = {\rm Pr}(A)\cdot {\rm Pr}(B).$$}} | ||
| − | *In | + | *In some applications, statistical independence is obvious, for example, in the "coin toss" experiment. The probability for "heads" or "tails" is independent of whether ''heads'' oder ''tails'' occurred in the last toss. |
| − | * | + | *And also the individual results in the random experiment "throwing a roulette ball" are always statistically independent of each other under fair conditions, even if individual system players do not want to admit this. |
| − | * | + | *In other applications, on the other hand, the question whether two events are statistically independent or not is not or only very difficult to answer instinctively. Here one can only arrive at the correct answer by checking the formal independence criterion given above, as the following example will show. |
| − | [[File:EN_Sto_T_1_3_S1.png|right|frame| | + | [[File:EN_Sto_T_1_3_S1.png|right|frame| Examples for statistically independent events]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 1:}$ |
| − | + | We consider the experiment "throwing two dice", where the two dice can be distinguished by their colors red $(R)$ and blue $(B)$ . | |
| − | + | The graph illustrates this fact, where the sum $S = R + B$ is entered in the two-dimensional field $(R, B)$ . | |
| − | + | For the following description we define the following events: | |
| − | *$A_1$: | + | *$A_1$: The number of eyes of the red die is $R < 4$ (red background) ⇒ ${\rm Pr}(A_1) = 1/2$, |
| − | *$A_2$: | + | *$A_2$: The number of eyes of the blue die is $B > 4$ (blaue Schrift) ⇒ ${\rm Pr}(A_2) = 1/3$, |
| − | *$A_3$: | + | *$A_3$: The sum of the two dice $S = 7$ (grüne Umrahmung) ⇒ ${\rm Pr}(A_3) = 1/6$, |
| − | *$A_4$: | + | *$A_4$: The sum of the two dice $S = 8$ ⇒ ${\rm Pr}(A_4) = 5/36$, |
| − | *$A_5$: | + | *$A_5$: The sum of the two dice $S = 10$ ⇒ ${\rm Pr}(A_5) = 3/36$. |
<br clear=all> | <br clear=all> | ||
| − | + | The graph can be interpreted as follows: | |
*Die beiden Ereignisse $A_1$ und $A_2$ sind statistisch unabhängig, da die Wahrscheinlichkeit ${\rm Pr}(A_1 ∩ A_2) = 1/6$ der Schnittmenge gleich dem Produkt der beiden Einzelwahrscheinlichkeiten ${\rm Pr}(A_1) = 1/2$ und ${\rm Pr}(A_2) = 1/3$ ist. Aufgrund der Aufgabenstellung hätte auch jedes andere Ergebnis sehr überrascht. | *Die beiden Ereignisse $A_1$ und $A_2$ sind statistisch unabhängig, da die Wahrscheinlichkeit ${\rm Pr}(A_1 ∩ A_2) = 1/6$ der Schnittmenge gleich dem Produkt der beiden Einzelwahrscheinlichkeiten ${\rm Pr}(A_1) = 1/2$ und ${\rm Pr}(A_2) = 1/3$ ist. Aufgrund der Aufgabenstellung hätte auch jedes andere Ergebnis sehr überrascht. | ||
*Aber auch die Ereignisse $A_1$ und $A_3$ sind wegen ${\rm Pr}(A_1) = 1/2$, ${\rm Pr}(A_3) = 1/6$ und ${\rm Pr}(A_1 ∩ A_3) = 1/12$ statistisch unabhängig. Die Wahrscheinlichkeit der Schnittmenge $(1/12)$ ergibt sich, weil drei der $36$ Felder sowohl rot hinterlegt als auch grün umrandet sind. | *Aber auch die Ereignisse $A_1$ und $A_3$ sind wegen ${\rm Pr}(A_1) = 1/2$, ${\rm Pr}(A_3) = 1/6$ und ${\rm Pr}(A_1 ∩ A_3) = 1/12$ statistisch unabhängig. Die Wahrscheinlichkeit der Schnittmenge $(1/12)$ ergibt sich, weil drei der $36$ Felder sowohl rot hinterlegt als auch grün umrandet sind. | ||
Revision as of 16:26, 25 November 2021
Contents
General Definition of Statistical Dependence
So far we have not paid much attention to statistical dependence between events, even though we have already used it as in the case of two disjoint sets: If an element belongs to $A$, it cannot with certainty also be contained in the disjoint set $B$ .
The strongest form of dependence at all is such a deterministic dependence between two sets or two events. Less pronounced is the statistical dependence. Let us start with its complement:
$\text{Definition:}$ Two events $A$ and $B$ are called statistically independent , if the probability of the intersection $A ∩ B$ is equal to the product of the individual probabilities:
- $${\rm Pr}(A \cap B) = {\rm Pr}(A)\cdot {\rm Pr}(B).$$
- In some applications, statistical independence is obvious, for example, in the "coin toss" experiment. The probability for "heads" or "tails" is independent of whether heads oder tails occurred in the last toss.
- And also the individual results in the random experiment "throwing a roulette ball" are always statistically independent of each other under fair conditions, even if individual system players do not want to admit this.
- In other applications, on the other hand, the question whether two events are statistically independent or not is not or only very difficult to answer instinctively. Here one can only arrive at the correct answer by checking the formal independence criterion given above, as the following example will show.
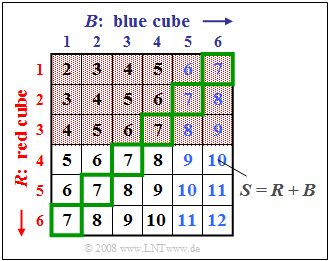
$\text{Example 1:}$ We consider the experiment "throwing two dice", where the two dice can be distinguished by their colors red $(R)$ and blue $(B)$ .
The graph illustrates this fact, where the sum $S = R + B$ is entered in the two-dimensional field $(R, B)$ .
For the following description we define the following events:
- $A_1$: The number of eyes of the red die is $R < 4$ (red background) ⇒ ${\rm Pr}(A_1) = 1/2$,
- $A_2$: The number of eyes of the blue die is $B > 4$ (blaue Schrift) ⇒ ${\rm Pr}(A_2) = 1/3$,
- $A_3$: The sum of the two dice $S = 7$ (grüne Umrahmung) ⇒ ${\rm Pr}(A_3) = 1/6$,
- $A_4$: The sum of the two dice $S = 8$ ⇒ ${\rm Pr}(A_4) = 5/36$,
- $A_5$: The sum of the two dice $S = 10$ ⇒ ${\rm Pr}(A_5) = 3/36$.
The graph can be interpreted as follows:
- Die beiden Ereignisse $A_1$ und $A_2$ sind statistisch unabhängig, da die Wahrscheinlichkeit ${\rm Pr}(A_1 ∩ A_2) = 1/6$ der Schnittmenge gleich dem Produkt der beiden Einzelwahrscheinlichkeiten ${\rm Pr}(A_1) = 1/2$ und ${\rm Pr}(A_2) = 1/3$ ist. Aufgrund der Aufgabenstellung hätte auch jedes andere Ergebnis sehr überrascht.
- Aber auch die Ereignisse $A_1$ und $A_3$ sind wegen ${\rm Pr}(A_1) = 1/2$, ${\rm Pr}(A_3) = 1/6$ und ${\rm Pr}(A_1 ∩ A_3) = 1/12$ statistisch unabhängig. Die Wahrscheinlichkeit der Schnittmenge $(1/12)$ ergibt sich, weil drei der $36$ Felder sowohl rot hinterlegt als auch grün umrandet sind.
- Dagegen bestehen zwischen den Ereignissen $A_1$ und $A_4$ statistische Bindungen, da die Wahrscheinlichkeit der Schnittmenge ⇒ ${\rm Pr}(A_1 ∩ A_4) = 1/18 = 4/72$ ungleich dem Produkt ${\rm Pr}(A_1) \cdot {\rm Pr}(A_4)= 1/2 \cdot 5/36 = 5/72$ ist.
- Die beiden Ereignisse $A_1$ und $A_5$ sind sogar disjunkt ⇒ ${\rm Pr}(A_1 ∩ A_5) = 0$: Keines der rot hinterlegten Felder ist mit $S=10$ beschriftet. Dieses Beispiel zeigt, dass Disjunktivität eine besonders ausgeprägte Form von statistischer Abhängigkeit ist.
Conditional Probability
Bestehen zwischen den beiden Ereignissen $A$ und $B$ statistische Bindungen, so ist durch die (unbedingten) Wahrscheinlichkeiten ${\rm Pr}(A)$ und ${\rm Pr}(B)$ der Sachverhalt im statistischen Sinne nicht eindeutig beschrieben. Man benötigt dann noch so genannte bedingte Wahrscheinlichkeiten.
$\text{Definitionen:}$ Die bedingte Wahrscheinlichkeit (englisch: Conditional Probability) von $A$ unter der Bedingung $B$ ist wie folgt berechenbar:
- $${\rm Pr}(A\hspace{0.05cm} \vert \hspace{0.05cm} B) = \frac{ {\rm Pr}(A \cap B)}{ {\rm Pr}(B)}.$$
In gleicher Weise gilt für die bedingte Wahrscheinlichkeit von $B$ unter der Bedingung $A$:
- $${\rm Pr}(B\hspace{0.05cm} \vert \hspace{0.05cm}A) = \frac{ {\rm Pr}(A \cap B)}{ {\rm Pr}(A)}.$$
Verknüpft man diese beiden Gleichungen, so ergibt sich der Satz von Bayes:
- $${\rm Pr}(B \hspace{0.05cm} \vert \hspace{0.05cm} A) = \frac{ {\rm Pr}(A\hspace{0.05cm} \vert \hspace{0.05cm} B)\cdot {\rm Pr}(B)}{ {\rm Pr}(A)}.$$
Nachfolgend sind einige Eigenschaften von bedingten Wahrscheinlichkeiten zusammengestellt:
- Auch eine bedingte Wahrscheinlichkeit liegt stets zwischen $0$ und $1$ einschließlich dieser beiden Grenzen: $0 \le {\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm} B) \le 1$.
- Kann die Bedingung $B$ als konstant angesehen werden, so gelten alle im Kapitel Mengentheoretische Grundlagen für die unbedingten Wahrscheinlichkeiten ${\rm Pr}(A)$ und ${\rm Pr}(B)$ angegebenen Rechenregeln weiterhin.
- Sind die existierenden Ereignisse $A$ und $B$ disjunkt, so ist ${\rm Pr}(A\hspace{0.05cm} | \hspace{0.05cm} B) = {\rm Pr}(B\hspace{0.05cm} | \hspace{0.05cm}A)= 0$.
- Ist $B$ eine echte oder unechte Teilmenge von $A$, so ist ${\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm} B) =1$.
- Sind zwei Ereignisse $A$ und $B$ statistisch voneinander unabhängig, so sind deren bedingte Wahrscheinlichkeiten gleich den unbedingten, wie folgende Rechnung zeigt:
- $${\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm} B) = \frac{{\rm Pr}(A \cap B)}{{\rm Pr}(B)} = \frac{{\rm Pr} ( A) \cdot {\rm Pr} ( B)} { {\rm Pr}(B)} = {\rm Pr} ( A).$$
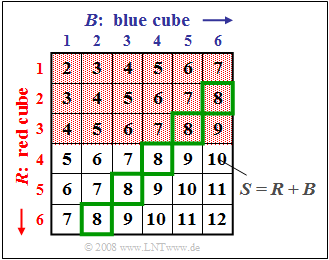
$\text{Beispiel 2:}$ Wir betrachten wieder das Zufallsexperiment "Werfen mit zwei Würfeln", wobei wie im $\text{Beispiel 1}$ $S = R + B$ die Summe des roten und des blauen Würfels bezeichnet.
Wir betrachten hier Bindungen zwischen den beiden Ereignissen
- $A_1$: Die Augenzahl des roten Würfels ist $R < 4$ (rote Hinterlegung) ⇒ ${\rm Pr}(A_1) = 1/2$,
- $A_4$: Die Summe der beiden Würfel ist $S = 8$ (grüne Umrahmung) ⇒ ${\rm Pr}(A_4) = 5/36$,
und nehmen nochmals Bezug auf das Ereignis
- $A_3$: Die Summe der beiden Würfel ist $S = 7$ ⇒ ${\rm Pr}(A_3) = 1/6$.
Zu dieser Grafik ist anzumerken:
- Zwischen den Ereignissen $A_1$ und $A_4$ bestehen statistische Bindungen, da die Wahrscheinlichkeit der Schnittmenge ⇒ ${\rm Pr}(A_1 ∩ A_4) = 2/36 = 4/72$ ungleich dem Produkt ${\rm Pr}(A_1) \cdot {\rm Pr}(A_4)= 1/2 \cdot 5/36 = 5/72$ ist.
- Die bedingte Wahrscheinlichkeit ${\rm Pr}(A_1 \hspace{0.05cm} \vert \hspace{0.05cm} A_4) = 2/5$ kann aus dem Quotienten der Verbundwahrscheinlichkeit ${\rm Pr}(A_1 ∩ A_4) = 2/36$ und der Wahrscheinlichkeit ${\rm Pr}(A_4) = 5/36$ berechnet werden.
- Da $A_1$ und $A_4$ statistisch abhängig sind, ist die bedingte Wahrscheinlichkeit ${\rm Pr}(A_1 \hspace{0.05cm}\vert \hspace{0.05cm} A_4) = 2/5$ (zwei der fünf grün umrandeten Felder sind rot hinterlegt) ungleich der absoluten Wahrscheinlichkeit ${\rm Pr}(A_1) = 1/2$ (die Hälfte aller Felder sind rot hinterlegt).
- Ebenso ist die bedingte Wahrscheinlichkeit ${\rm Pr}(A_4 \hspace{0.05cm} \vert \hspace{0.05cm} A_1) = 2/18 = 4/36$ (zwei der $18$ rot hinterlegten Felder sind grün umrandet) ungleich der absoluten Wahrscheinlichkeit ${\rm Pr}(A_4) = 5/36$ (insgesamt sind fünf der $36$ Felder grün umrandet).
- Dieses letzte Ergebnis lässt sich zum Beispiel auch über den Satz von Bayes ableiten:
- $${\rm Pr}(A_4 \hspace{0.05cm} \vert\hspace{0.05cm} A_1) = \frac{ {\rm Pr}(A_1 \hspace{0.05cm} \vert\hspace{0.05cm} A_4)\cdot {\rm Pr} ( A_4)} { {\rm Pr}(A_1)} = \frac{2/5 \cdot 5/36}{1/2} = 1/9.$$
- Dagegen gelten für $A_1$ und das hierzu statistisch unabhängige Ereignis $A_3$ die folgenden bedingten Wahrscheinlichkeiten, siehe Beispiel 1:
- $${\rm Pr}(A_{\rm 1} \hspace{0.05cm}\vert \hspace{0.05cm} A_{\rm 3}) = {\rm Pr}(A_{\rm 1}) = \rm 1/2\hspace{0.5cm}{\rm bzw.}\hspace{0.5cm}{\rm Pr}(A_{\rm 3} \hspace{0.05cm} \vert \hspace{0.05cm} A_{\rm 1}) = {\rm Pr}(A_{\rm 3}) = 1/6.$$
Allgemeines Multiplikationstheorem
Wir betrachten mehrere Ereignisse, die als $A_i$ mit $1 ≤ i ≤ I$ bezeichnet werden. Diese Ereignisse $A_i$ stellen nun aber kein vollständiges System mehr dar, das heißt,
- sie sind nicht paarweise zueinander disjunkt, und
- es können zwischen den einzelnen Ereignissen auch statistische Bindungen bestehen.
$\text{Definition:}$ Für die so genannte Verbundwahrscheinlichkeit, also für die Wahrscheinlichkeit der Schnittmenge aller $I$ Ereignisse $A_i$, gilt in diesem Fall:
- $${\rm Pr}(A_{\rm 1} \cap \hspace{0.02cm}\text{ ...}\hspace{0.1cm} \cap A_{I}) = {\rm Pr}(A_{I})\hspace{0.05cm}\cdot\hspace{0.05cm}{\rm Pr}(A_{I \rm -1} \hspace{0.05cm}\vert \hspace{0.05cm} A_I) \hspace{0.05cm}\cdot \hspace{0.05cm}{\rm Pr}(A_{I \rm -2} \hspace{0.05cm}\vert\hspace{0.05cm} A_{I - \rm 1}\cap A_I)\hspace{0.05cm} \cdot \hspace{0.02cm}\text{ ...} \hspace{0.1cm} \cdot\hspace{0.05cm} {\rm Pr}(A_{\rm 1} \hspace{0.05cm}\vert \hspace{0.05cm}A_{\rm 2} \cap \hspace{0.02cm}\text{ ...} \hspace{0.1cm}\cap A_{ I}).$$
In gleicher Weise gilt natürlich auch:
- $${\rm Pr}(A_{\rm 1} \cap \hspace{0.02cm}\text{ ...}\hspace{0.1cm} \cap A_{I}) = {\rm Pr}(A_1)\hspace{0.05cm}\cdot\hspace{0.05cm}{\rm Pr}(A_2 \hspace{0.05cm}\vert \hspace{0.05cm} A_1) \hspace{0.05cm}\cdot \hspace{0.05cm}{\rm Pr}(A_3 \hspace{0.05cm}\vert \hspace{0.05cm} A_1\cap A_2)\hspace{0.05cm} \cdot \hspace{0.02cm}\text{ ...}\hspace{0.1cm} \cdot\hspace{0.05cm} {\rm Pr}(A_I \hspace{0.05cm}\vert \hspace{0.05cm}A_1 \cap \hspace{0.02cm} \text{ ...} \hspace{0.1cm}\cap A_{ I-1}).$$
$\text{Beispiel 3:}$ Eine Lostrommel enthält zehn Lose, darunter drei Treffer $($Ereignis $T_1)$. Dann gilt für die Wahrscheinlichkeit, dass man mit zwei Losen zwei Treffer zieht:
- $${\rm Pr}(T_1 \cap T_2) = {\rm Pr}(T_1) \cdot {\rm Pr}(T_2 \hspace{0.05cm }\vert \hspace{0.05cm} T_1) = 3/10 \cdot 2/9 = 1/15 \approx 6.7 \%.$$
- Hierbei ist berücksichtigt, dass sich bei der zweiten Ziehung $($Ereignis $T_2)$ nur mehr neun Lose und zwei Treffer in der Urne befänden, falls im ersten Durchgang ein Treffer gezogen worden ist ⇒ ${\rm Pr}(T_2 \hspace{0.05cm} \vert\hspace{0.05cm} T_1) = 2/9$ .
- Würde man jedoch die Lose nach der Ziehung wieder in die Trommel zurücklegen, so wären die Ereignisse $T_1$ und $T_2$ statistisch unabhängig und es würde gelten:
- $$ {\rm Pr}(T_1 ∩ T_2) = (3/10)^2 = 9\%.$$
Rückschlusswahrscheinlichkeit
Gegeben seien wieder Ereignisse $A_i$ mit $1 ≤ i ≤ I$, die ein vollständiges System bilden. Das heißt:
- Alle Ereignisse sind paarweise disjunkt $(A_i ∩ A_j = ϕ$ für alle $i ≠ j$ ).
- Die Vereinigungsmenge ergibt die Grundmenge:
- $$\rm \bigcup_{\it i=1}^{\it I}\it A_i = \it G.$$
Daneben betrachten wir noch das Ereignis $B$, von dem alle bedingten Wahrscheinlichkeiten ${\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm} A_i)$ mit den Indizes $1 ≤ i ≤ I$ bekannt sind.
$\text{Satz von der totalen Wahrscheinlichkeit:}$ Unter den oben genannten Voraussetzungen gilt für die (unbedingte) Wahrscheinlichkeit des Ereignisses $B$:
- $${\rm Pr}(B) = \sum_{i={\rm1} }^{I}{\rm Pr}(B \cap A_i) = \sum_{i={\rm1} }^{I}{\rm Pr}(B \hspace{0.05cm} \vert\hspace{0.05cm} A_i)\cdot{\rm Pr}(A_i).$$
$\text{Definition:}$ Aus dieser Gleichung folgt mit dem Satz von Bayes für die Rückschlusswahrscheinlichkeit:
- $${\rm Pr}(A_i \hspace{0.05cm} \vert \hspace{0.05cm} B) = \frac{ {\rm Pr}( B \mid A_i)\cdot {\rm Pr}(A_i )}{ {\rm Pr}(B)} = \frac{ {\rm Pr}(B \hspace{0.05cm} \vert \hspace{0.05cm} A_i)\cdot {\rm Pr}(A_i )}{\sum_{k={\rm1} }^{I}{\rm Pr}(B \hspace{0.05cm} \vert \hspace{0.05cm} A_k)\cdot{\rm Pr}(A_k) }.$$
$\text{Beispiel 4:}$ In Münchner Studentenheimen wohnen Studierende
- der Ludwig–Maximilian–Universität $($Ereignis $L$ ⇒ ${\rm Pr}(L) = 70\%)$ und
- der Technischen Universität München $($Ereignis $T$ ⇒ ${\rm Pr}(T) = 30\%)$.
Es ist weiterhin bekannt, dass an der LMU $60\%$ aller Studierenden weiblich sind, an der TUM nur $10\%$.
- Der Anteil aller Studentinnen im Studentenheim $($Ereignis $W)$ kann dann mit dem Satz von der totalen Wahrscheinlichkeit ermittelt werden:
- $${\rm Pr}(W) = {\rm Pr}(W \hspace{0.05cm} \vert \hspace{0.05cm} L)\hspace{0.01cm}\cdot\hspace{0.01cm}{\rm Pr}(L) \hspace{0.05cm}+\hspace{0.05cm} {\rm Pr}(W \hspace{0.05cm} \vert \hspace{0.05cm} T)\hspace{0.01cm}\cdot\hspace{0.01cm}{\rm Pr}(T) = \rm 0.6\hspace{0.01cm}\cdot\hspace{0.01cm}0.7\hspace{0.05cm}+\hspace{0.05cm}0.1\hspace{0.01cm}\cdot \hspace{0.01cm}0.3 = 45 \%.$$
- Trifft man eine Studentin, so kann man mit der Rückschlusswahrscheinlichkeit
- $${\rm Pr}(L \hspace{-0.05cm}\mid \hspace{-0.05cm}W) = \frac{ {\rm Pr}(W \hspace{-0.05cm}\mid \hspace{-0.05cm}L)\cdot {\rm Pr}(L) }{ {\rm Pr}(W \hspace{-0.05cm}\mid \hspace{-0.05cm}L) \cdot {\rm Pr}(L) +{\rm Pr}(W \hspace{-0.05cm}\mid \hspace{-0.05cm}T) \cdot {\rm Pr}(T)}=\rm \frac{0.6\cdot 0.7}{0.6\cdot 0.7 + 0.1\cdot 0.3}=\frac{14}{15}\approx 93.3 \%$$
- vorhersagen, dass sie an der LMU studieren wird. Ein durchaus realistisches Ergebnis (zumindest in der Vergangenheit).
Die Aussagen dieses Abschnitts sind im Lernvideo Statistische Abhängigkeit und Unabhängigkeit zusammengefasst.
Aufgaben zum Kapitel
Aufgabe 1.4: 2S/3E-Kanalmodell
Aufgabe 1.4Z: Summe von Ternärgrößen
Aufgabe 1.5Z: Ausfallwahrscheinlichkeiten