Binomial and Poisson Distribution (Applet)
Open Applet in new Tab English Applet with German WIKI description
Contents
Applet Description
This applet allows the calculation and graphical display of
- the probabilities ${\rm Pr}(z=\mu)$ of a discrete random variable $z \in \{\mu \} = \{0, 1, 2, 3, \text{...} \}$, that determine its Probability Density Function (PDF) – here representation with Dirac delta functions ${\rm \delta}( z-\mu)$:
- $$f_{z}(z)=\sum_{\mu=1}^{M}{\rm Pr}(z=\mu)\cdot {\rm \delta}( z-\mu),$$
- the probabilities ${\rm Pr}(z \le \mu)$ of the Cumulative Distribution Function (CDF):
- $$F_{z}(\mu)={\rm Pr}(z\le\mu).$$
Discrete distributions are available in two sets of parameters:
- the Binomial distribution with the parameters $I$ and $p$ ⇒ $z \in \{0, 1, \text{...} \ , I \}$ ⇒ $M = I+1$ possible values,
- the Poisson distribution with the parameter $\lambda$ ⇒ $z \in \{0, 1, 2, 3, \text{...}\}$ ⇒ $M \to \infty$.
In the exercises below you will be able to compare:
- two Binomial distributions with different sets of parameters $I$ and $p$,
- two Poisson distributions with different rates $\lambda$,
- a Binomial distribution with a Poisson distribution.
Theoretical Background
Properties of the Binomial Distribution
The Binomial distribution represents an important special case for the likelihood of occurence of a discrete random variable. For the derivation we assume, that $I$ binary and statistically independent random variables $b_i \in \{0, 1 \}$ can take
- the value $1$ with the probability ${\rm Pr}(b_i = 1) = p$, and
- the value $0$ with the probability ${\rm Pr}(b_i = 0) = 1-p$.
The sum
- $$z=\sum_{i=1}^{I}b_i$$
is also a discrete random variable with symbols from the set $\{0, 1, 2, \cdots\ , I\}$ with size $M = I + 1$ and is called "binomially distributed".
Probabilities of the Binomial Distribution
The probabilities to find $z = \mu$ for $μ = 0, \text{...}\ , I$ are given as
- $$p_\mu = {\rm Pr}(z=\mu)={I \choose \mu}\cdot p^\mu\cdot ({\rm 1}-p)^{I-\mu},$$
with the number of combinations $(I \text{ over }\mu)$:
- $${I \choose \mu}=\frac{I !}{\mu !\cdot (I-\mu) !}=\frac{ {I\cdot (I- 1) \cdot \ \cdots \ \cdot (I-\mu+ 1)} }{ 1\cdot 2\cdot \ \cdots \ \cdot \mu}.$$
Moments of the Binomial Distribution
Consider a binomially distributed random variable $z$ and its expected value of order $k$:
- $$m_k={\rm E}[z^k]=\sum_{\mu={\rm 0}}^{I}\mu^k\cdot{I \choose \mu}\cdot p^\mu\cdot ({\rm 1}-p)^{I-\mu}.$$
We can derive the formulas for
- the linear average: $m_1 = I\cdot p,$
- the second moment: $m_2 = (I^2-I)\cdot p^2+I\cdot p,$
- the variance and standard deviation: $\sigma^2 = {m_2 - m_1^2} = {I \cdot p\cdot (1-p)} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \sigma = \sqrt{I \cdot p\cdot (1-p)}.$
Applications of the Binomial Distribution
The Binomial distribution has a variety of uses in telecommunications as well as in other disciplines:
- It characterizes the distribution of rejected parts (Ausschussstücken) in statistical quality control.
- The simulated bit error rate of a digital transmission system is technically a binomially distributed random variable.
- The binomial distribution can be used to calculate the residual error probability with blockwise coding, as the following example shows.
$\text{Example 1:}$ When transfering blocks of $I =5$ binary symbols through a channel, that
- distorts a symbol with probability $p = 0.1$ ⇒ random variable $e_i = 1$, and
- transfers the symbol undistorted with probability $1 - p = 0.9$ ⇒ random variable $e_i = 0$,
the new random variable $f$ ("error per block") calculates to:
- $$f=\sum_{i=1}^{I}e_i.$$
$f$ can now take integer values between $\mu = 0$ (all symbols are correct) and $\mu = I = 5$ (all five symbols are erroneous). We describe the probability of $\mu$ errors as $p_μ = {\rm Pr}(f = \mu)$.
- The case that all five symbols are transmitted correctly occurs with the probability of $p_0 = 0.9^{5} ≈ 0.5905$. This can also be seen from the binomial formula for $μ = 0$ , considering the definition $5\text{ over } 0 = 1$.
- A single error $(f = 1)$ occurs with the probability $p_1 = 5\cdot 0.1\cdot 0.9^4\approx 0.3281$. The first factor indicates, that there are $5\text{ over } 1 = 5$ possibe error positions. The other two factors take into account, that one symbol was erroneous and the other four are correct when $f =1$.
- For $f =2$ there are $5\text{ over } 2 = (5 \cdot 4)/(1 \cdot 2) = 10$ combinations and you get a probability of $p_2 = 10\cdot 0.1^2\cdot 0.9^3\approx 0.0729$.
If a block code can correct up to two errors, the residual error probability is $p_{\rm R} = 1-p_{\rm 0}-p_{\rm 1}-p_{\rm 2}\approx 0.85\%$.
A second calculation option would be $p_{\rm R} = p_{3} + p_{4} + p_{5}$ with the approximation $p_{\rm R} \approx p_{3} = 0.81\%.$
The average number of errors in a block is $m_f = 5 \cdot 0.1 = 0.5$ and the variance of the random variable $f$ is $\sigma_f^2 = 5 \cdot 0.1 \cdot 0.9= 0.45$ ⇒ standard deviation $\sigma_f \approx 0.671.$
Properties of the Poisson Distribution
The Poisson distribution is a special case of the Binomial distribution, where
- $I → \infty$ and $p →0$.
- Additionally, the parameter $λ = I · p$ must be finite.
The parameter $λ$ indicates the average number of "ones" in a specified time unit and is called rate.
Unlike the Binomial distribution where $0 ≤ μ ≤ I$, here, the random variable can assume arbitrarily large non-negative integers, which means that the number of possible values is not countable. However, since no intermediate values can occur, the Poisson distribution is still a "discrete distribution".
Probabilities of the Poisson Distribution
With the limits $I → \infty$ and $p →0$, the likelihood of occurence of the Poisson distributed random variable $z$ can be derived from the probabilities of the Binomial distribution:
- $$p_\mu = {\rm Pr} ( z=\mu ) = \lim_{I\to\infty} \cdot \frac{I !}{\mu ! \cdot (I-\mu )!} \cdot (\frac{\lambda}{I} )^\mu \cdot ( 1-\frac{\lambda}{I})^{I-\mu}.$$
After some algebraic transformations we finally obtain
- $$p_\mu = \frac{ \lambda^\mu}{\mu!}\cdot {\rm e}^{-\lambda}.$$
Moments of the Poisson Distribution
The moments of the Poisson distribution can be derived directly from the corresponding equations of the Binomial distribution by taking the limits again:
- $$m_1 =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty, \hspace{0.2cm} {p\hspace{0.05cm}\to\hspace{0.05cm} 0}}\right.} \hspace{0.2cm} I \cdot p= \lambda,\hspace{0.8cm} \sigma =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty, \hspace{0.2cm} {p\hspace{0.05cm}\to\hspace{0.05cm} 0}}\right.} \hspace{0.2cm} \sqrt{I \cdot p \cdot (1-p)} = \sqrt {\lambda}.$$
We can see that for the Poisson distribution $\sigma^2 = m_1 = \lambda$ always holds. In contrast, the moments of the Binomial distribution always fulfill $\sigma^2 < m_1$.
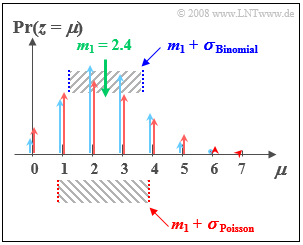
$\text{Example 2:}$ We now compare the Binomial distribution with parameters $I =6$ und $p = 0.4$ with the Poisson distribution with $λ = 2.4$:
- Both distributions have the same linear average $m_1 = 2.4$.
- The standard deviation of the Poisson distribution (marked red in the figure) is $σ ≈ 1.55$.
- The standard deviation of the Binomial distribution (marked blue) is $σ = 1.2$.
Applications of the Poisson Distribution
The Poisson distribution is the result of a so-called Poisson point process which is often used as a model for a series of events that may occur at random times. Examples of such events are
- failure of devices - an important task in reliability theory,
- shot noise in the optical transmission simulations, and
- the start of conversations in a telephone relay center („Teletraffic engineering”).
$\text{Example 3:}$ A telephone relay receives ninety requests per minute on average $(λ = 1.5 \text{ per second})$. The probabilities $p_µ$, that in an arbitrarily large time frame exactly $\mu$ requests are received, is:
- $$p_\mu = \frac{1.5^\mu}{\mu!}\cdot {\rm e}^{-1.5}.$$
The resulting numerical values are $p_0 = 0.223$, $p_1 = 0.335$, $p_2 = 0.251$, etc.
From this, additional parameters can be derived:
- The distance $τ$ between two requests satisfies the "exponential distribution",
- The mean time span between two requests is ${\rm E}[τ] = 1/λ ≈ 0.667 \ \rm s$.
Comparison of Binomial and Poisson Distribution
This section deals with the similarities and differences between Binomial and Poisson distributions.
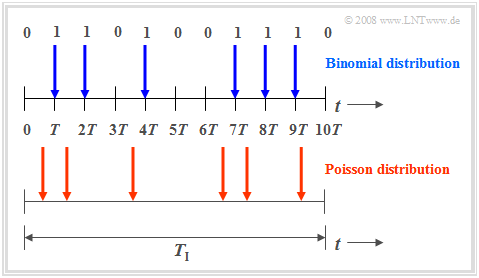
The Binomial distribution is used to describe stochastic events, that have a fixed period $T$. For example the period of an ISDN (Integrated Services Digital Network) network with $64 \ \rm kbit/s$ is $T \approx 15.6 \ \rm \mu s$.
- Binary events such as the error-free $(e_i = 0)$/ faulty $(e_i = 1)$ transmission of individual symbols only occur in this time frame.
- With the Binomial distribution, it is possible to make statistical statements about the number of expected erros in a period $T_{\rm I} = I · T$, as is shown in the time figure above (marked blue).
- For very large values of $I$ and very small values of $p$, the Binomial distribution can be approximated by the Poisson distribution with rate $\lambda = I \cdot p$.
- If at the same time $I · p \gg 1$, the Poisson distribution as well as the Binomial distribution turn into a discrete Gaussian distribution according to the de Moivre-Laplace Theorem.
The Poisson distribution can also be used to make statements about the number of occuring binary events in a finite time interval.
By assuming the same observation period $T_{\rm I}$ and increasing the number of partial periods $I$, the period $T$, in which a new event ($0$ or $1$) can occur, gets smaller and smaller. In the limit where $T$ goes to zero, this means:
- With the Poisson distribution binary events can not only occur at certain given times, but at any time, which is illustrated in the second time chart.
- In order to get the same number of "ones" in the period $T_{\rm I}$ - in average - as in the Binomial distribution (six pulses in the example), the characteristic probability $p = {\rm Pr}( e_i = 1)$ for an infinitesimal small time interval $T$ must go to zero.
Exercises
- First select the number $(1,\text{...}, 7)$ of the exercise. The number $0$ corresponds to a "Reset": Same setting as at program start.
- A task description is displayed. The parameter values are adjusted. Solution after pressing "Show solution".
- In these exercises, the term Blue refers to distribution function 1 (marked blue in the applet) and the term Red refers to distribution function 2 (marked red in applet).
(1) Set Blue to Binomial distribution $(I=5, \ p=0.4)$ and Red to Binomial distribution $(I=10, \ p=0.2)$.
- What are the probabilities ${\rm Pr}(z=0)$ and ${\rm Pr}(z=1)$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Blue: }{\rm Pr}(z=0)=0.6^5=7.78\%, \hspace{0.3cm}{\rm Pr}(z=1)=0.4 \cdot 0.6^4=25.92\%;$
$\hspace{1.85cm}\text{Red: }{\rm Pr}(z=0)=0.8^{10}=10.74\%, \hspace{0.3cm}{\rm Pr}(z=1)=0.2 \cdot 0.8^9=26.84\%.$
(2) Using the same settings as in (1), what are the probabilities ${\rm Pr}(3 \le z \le 5)$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Note that }{\rm Pr}(3 \le z \le 5) = {\rm Pr}(z=3) + {\rm Pr}(z=4) + {\rm Pr}(z=5)\text{, or }
{\rm Pr}(3 \le z \le 5) = {\rm Pr}(z \le 5) - {\rm Pr}(z \le 2)$
$\hspace{1.85cm}\text{Blue: }{\rm Pr}(3 \le z \le 5) = 0.2304+ 0.0768 + 0.0102 =1 - 0.6826 = 0.3174;$
$\hspace{1.85cm}\text{Red: }{\rm Pr}(3 \le z \le 5) = 0.2013 + 0.0881 + 0.0264 = 0.9936 - 0.6778 = 0.3158.$
(3) Using the same settings as in (1), what are the differences in the linear average $m_1$ and the standard deviation $\sigma$ between the two Binomial distributions?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Average:}\hspace{0.2cm}m_\text{1} = I \cdot p\hspace{0.3cm} \Rightarrow\hspace{0.3cm} m_\text{1, Blue} = 5 \cdot 0.4\underline{ = 2 =} \ m_\text{1, Red} = 10 \cdot 0.2; $
$\hspace{1.85cm}\text{Standard deviation:}\hspace{0.4cm}\sigma = \sqrt{I \cdot p \cdot (1-p)} = \sqrt{m_1 \cdot (1-p)}\hspace{0.3cm}\Rightarrow\hspace{0.3cm} \sigma_{\rm Blue} = \sqrt{2 \cdot 0.6} =1.095 < \sigma_{\rm Red} = \sqrt{2 \cdot 0.8} = 1.265.$
(4) Set Blue to Binomial distribution $(I=15, p=0.3)$ and Red to Poisson distribution $(\lambda=4.5)$.
- What differences arise between both distributions regarding the average $m_1$ and variance $\sigma^2$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Both distributions have the same average:}\hspace{0.2cm}m_\text{1, Blue} = I \cdot p\ = 15 \cdot 0.3\hspace{0.15cm}\underline{ = 4.5 =} \ m_\text{1, Red} = \lambda$;
$\hspace{1.85cm} \text{Binomial distribution: }\hspace{0.2cm} \sigma_\text{Blue}^2 = m_\text{1, Blue} \cdot (1-p)\hspace{0.15cm}\underline { = 3.15} < \text{Poisson distribution: }\hspace{0.2cm} \sigma_\text{Red}^2 = \lambda\hspace{0.15cm}\underline { = 4.5}$;
(5) Using the same settings as in (4), what are the probabilities ${\rm Pr}(z \gt 10)$ and ${\rm Pr}(z \gt 15)$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{Binomial: }\hspace{0.2cm} {\rm Pr}(z \gt 10) = 1 - {\rm Pr}(z \le 10) = 1 - 0.9993 = 0.0007;\hspace{0.3cm} {\rm Pr}(z \gt 15) = 0 \ {\rm (exactly)}$.
$\hspace{1.85cm}\text{Poisson: }\hspace{0.2cm} {\rm Pr}(z \gt 10) = 1 - 0.9933 = 0.0067;\hspace{0.3cm}{\rm Pr}(z \gt 15) \gt 0\hspace{0.2cm}( \approx 0)$;
$\hspace{1.85cm}\text{Approximation: }\hspace{0.2cm}{\rm Pr}(z \gt 15) \ge {\rm Pr}(z = 16) = \lambda^{16} /{16!}\approx 2 \cdot 10^{-22}$
(6) Using the same settings as in (4), which parameters lead to a symmetric distribution around $m_1$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{Binomial distribution with }p = 0.5\text{: }p_\mu = {\rm Pr}(z = \mu)\text{ symmetric around } m_1 = I/2 = 7.5 \ ⇒ \ p_μ = p_{I–μ}\ ⇒ \ p_8 = p_7, \ p_9 = p_6, \text{etc.}$
$\hspace{1.85cm}\text{In contrast, the Poisson distribution is never symmetric, since it extends to infinity!}$
Applet Manual
(A) Preselection for blue parameter set
(B) Parameter input: Sliders $I$ and $p$
(C) Preselection for Red parameter set
(D) Parameter input: Slider $\lambda$
(E) Graphic display of the Distribution
(F) Output of moments for blue parameter set
(G) Output of moments for redparameter set
(H) Variation possibilities for the graphic display
$\hspace{1.5cm}$"$+$" (Zoom in),
$\hspace{1.5cm}$ "$-$" (Zoom out)
$\hspace{1.5cm}$ "$\rm o$" (Reset)
$\hspace{1.5cm}$ "$\leftarrow$" (Move left), etc.
( I ) Output of ${\rm Pr} (z = \mu)$ and ${\rm Pr} (z \le \mu)$
(J) Exercises: Exercise selection, description and solution
Other options for graphic display:
- Hold shift and scroll: Zoom in on/out of coordinate system,
- Hold shift and left click: Move the coordinate system.
About the Authors
This interactive calculation was designed and realized at the Lehrstuhl für Nachrichtentechnik of the Technische Universität München.
- The original version was created in 2003 by Ji Li as part of her Diploma thesis using "FlashMX–Actionscript" (Supervisor: Günter Söder).
- In 2018 this Applet was redesigned and updated to "HTML5" by Jimmy He as part of his Bachelor's thesis (Supervisor: Tasnád Kernetzky) .
Once again: Open Applet in new Tab
Open Applet in new Tab English Applet with German WIKI description