Discrete Fouriertransform and Inverse
Open Applet in new Tab Deutsche Version Öffnen
Contents
- 1 Applet Description
- 2 Theoretical Background
- 2.1 Arguments for the discrete realization of the Fourier transform
- 2.2 Time discretization – periodization in the frequency domain
- 2.3 Frequency discretization – periodization in the time domain
- 2.4 Finite signal representation
- 2.5 Discrete Fourier Transform
- 2.6 Inverse Discrete Fourier Transform
- 2.7 Interpretation of DFT and IDFT
- 3 Exercises
- 4 Applet Manual
- 5 About the Authors
- 6 Once again: Open Applet in new Tab
Applet Description
The conventional »Fourier Transform« $\rm (FT)$ allows the calculation of the spectral function $X(f)$ of a time-continuous signal $x(t)$.
In contrast, the »Discrete Fourier Transform« $\rm (DFT)$ is limited to a time-discrete signal, represented by $N$ time domain coefficients $d(\nu)$ with indices $\nu = 0, \text{...} , N\hspace{-0.1cm}-\hspace{-0.1cm}1$, which can be interpreted as equidistant samples of the time-continuous signal $x(t)$.
If the »sampling theorem« is fulfilled, the DFT algorithm likewise allows the calculation of $N$ frequency domain coefficients $D(\mu)$ with indices $\mu = 0, \text{...} , N\hspace{-0.1cm}-\hspace{-0.1cm}1$. These are equidistant samples of the frequency-continuous spectrum $X(f)$.
- The applet illustrates the properties of the $\text{DFT:}\hspace{0.3cm}d(\nu)\hspace{0.1cm} \Rightarrow \hspace{0.1cm} D(\mu)$ by using the example $N=16$. The default $d(\nu)$ assignments for the DFT are:
- $\rm (a)$ According to the input field, $\rm (b)$ Constant signal, $\rm (c)$ Complex exponential time function , $\rm (d)$ Harmonic oscillation $($with phase $\varphi = 45^\circ)$,
- $\rm (e)$ Cosine signal $($one period$)$, $\rm (f)$ Sinusoidal signal $($one period$)$, $\rm (g)$ Cosine signal $($two periods$)$, $\rm (h)$ Alternating time coefficients,
- $\rm (i)$ Dirac delta impulse, $\rm (j)$ Rectangular pulse , $\rm (k)$ Triangular pulse, $\rm (l)$ Gaussian pulse.
- Possible $D(\mu)$ assignments for the Inverse Discrete Fourier Transform ⇒ $\text{IDFT:}\hspace{0.3cm}D(\mu)\hspace{0.1cm} \Rightarrow \hspace{0.1cm} d(\nu)$ are:
- $\rm (A)$ According to the input field, $\rm (B)$ Constant spectrum, $\rm (C)$ Complex exponential function (of frequency), $\rm (D)$ Equivalent to setting $\rm (d)$ in the time domain,
- $\rm (E)$ Cosine spectrum $($one frequency period$)$, $\rm (F)$ Sinusoidal spectrum $($one frequency period$)$, $\rm (G)$ Cosine spectrum $($two frequency periods$)$,
- $\rm (H)$ Alternating spectral coefficients, $\rm (I)$ Dirac delta spectrum, $\rm (J)$ Rectangular spectrum, $\rm (K)$ Triangular spectrum, $\rm (L)$ Gaussian spectrum.
The applet uses the framework »Plot.ly«.
Theoretical Background
Arguments for the discrete realization of the Fourier transform
The »Fourier transform« according to the conventional description for continuous-time signals has an infinitely high selectivity due to the unlimited extension of the integration interval and is therefore an ideal theoretical tool for spectral analysis.
If the spectral components $X(f)$ of a time function $x(t)$ are to be determined numerically, the general transformation equations
- $$\begin{align*}X(f) & = \int_{-\infty }^{+\infty}x(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi f t}\hspace{0.1cm} {\rm d}t\hspace{0.5cm} \Rightarrow\hspace{0.5cm} \text{Forward transformation}\hspace{0.7cm} \Rightarrow\hspace{0.5cm} \text{First Fourier integral} \hspace{0.05cm},\\ x(t) & = \int_{-\infty }^{+\infty}\hspace{-0.15cm}X(f) \cdot {\rm e}^{\hspace{0.05cm}+{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi f t}\hspace{0.1cm} {\rm d}f\hspace{0.35cm} \Rightarrow\hspace{0.5cm} \text{Backward transformation}\hspace{0.4cm} \Rightarrow\hspace{0.5cm} \text{Second Fourier integral} \hspace{0.05cm}\end{align*}$$
are unsuitable for two reasons:
- The equations apply exclusively to continuous-time signals. With digital computers or signal processors, however, only discrete-time signals can be processed.
- For a numerical evaluation of the two Fourier integrals it is necessary to limit the respective integration interval to a finite value.
$\text{This results in the following consequence:}$
A »continuous-time signal« must undergo two processes before the numerical determination of its spectral properties, viz.
- »sampling« for discretization, and
- »windowing« to limit the integration interval.
In the following, starting from an aperiodic time function $x(t)$ and the corresponding Fourier spectrum $X(f)$, a discrete-time and discrete-frequency description suitable for computer processing is presented.
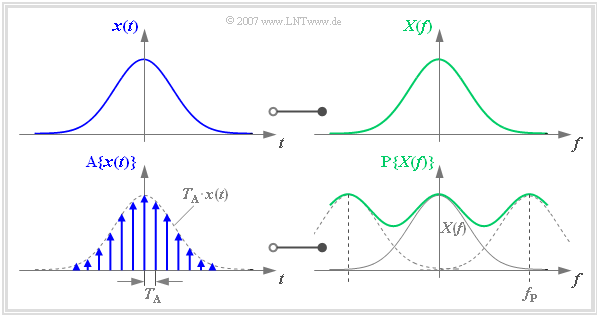
Time discretization – periodization in the frequency domain
The following graphs uniformly show the time domain on the left and the frequency domain on the right. Without restriction of generality, $x(t)$ and $X(f)$ are real and Gaussian, respectively.
One can describe the sampling of the time signal $x(t)$ by multiplication with a Dirac delta pulse $p_{\delta}(t)$. This results in the time signal sampled at distance $T_{\rm A}$:
- $${\rm A}\{x(t)\} = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot x(\nu \cdot T_{\rm A})\cdot \delta (t- \nu \cdot T_{\rm A} )\hspace{0.05cm}.$$
We now transform this sampled signal $\text{A}\{ x(t)\}$ into the frequency domain. The multiplication of the Dirac delta pulse $p_{\delta}(t)$ with $x(t)$ corresponds in the frequency domain to the convolution of $P_{\delta}(f)$ with $X(f)$. The periodized spectrum $\text{P}\{ X(f)\}$ is obtained, where $f_{\rm P}$ is the frequency period of the function $\text{P}\{ X(f)\}$:
- $${\rm A}\{x(t)\} \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} {\rm P}\{X(f)\} = \sum_{\mu = - \infty }^{+\infty} X (f- \mu \cdot f_{\rm P} )\hspace{0.5cm} {\rm with }\hspace{0.5cm}f_{\rm P}= {1}/{T_{\rm A}}\hspace{0.05cm}.$$
- We call the sampled signal $\text{A}\{ x(t)\}$.
- The »frequency period« is denoted by $f_{\rm P}$ = $1/T_{\rm A}$.
The graph above shows the functional relationship described here. It should be noted:
- The frequency period $f_{\rm P}$ was deliberately chosen small here so that the overlap of the spectra to be summed can be clearly seen.
- In practice, due to the sampling theorem, $f_{\rm P}$ should be at least twice as large as the largest frequency contained in the signal $x(t)$.
- If this is not fulfilled, »aliasing« must be expected.
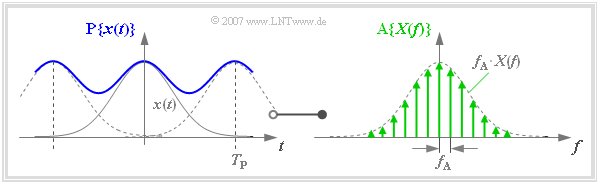
Frequency discretization – periodization in the time domain
The discretization of $X(f)$ can also be described by a multiplication with a Dirac delta pulse. The result is the spectrum sampled at distance $f_{\rm A}$:
- $${\rm A}\{X(f)\} = X(f) \cdot \sum_{\mu = - \infty }^{+\infty} f_{\rm A} \cdot \delta (f- \mu \cdot f_{\rm A } ) = \sum_{\mu = - \infty }^{+\infty} f_{\rm A} \cdot X(\mu \cdot f_{\rm A } ) \cdot\delta (f- \mu \cdot f_{\rm A } )\hspace{0.05cm}.$$
- Transforming the frequency Dirac delta pulse used here $($with pulse weights $f_{\rm A})$ into the time domain, we obtain with $T_{\rm P} = 1/f_{\rm A}$:
- $$\sum_{\mu = - \infty }^{+\infty} f_{\rm A} \cdot \delta (f- \mu \cdot f_{\rm A } ) \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} \sum_{\nu = - \infty }^{+\infty} \delta (t- \nu \cdot T_{\rm P } ) \hspace{0.05cm}.$$
- The multiplication with $X(f)$ corresponds in the time domain to the convolution with $x(t)$. The signal $\text{P}\{ x(t)\}$ periodized at distance $T_{\rm P}$ is obtained:
- $${\rm A}\{X(f)\} \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} {\rm P}\{x(t)\} = x(t) \star \sum_{\nu = - \infty }^{+\infty} \delta (t- \nu \cdot T_{\rm P } )= \sum_{\nu = - \infty }^{+\infty} x (t- \nu \cdot T_{\rm P } ) \hspace{0.05cm}.$$
$\text{Example 1:}$ This relationship is illustrated in the graph:
- Due to the coarse frequency rastering, this example results in a relatively small value for the time period $T_{\rm P}$.
- Therefore, the $($blue$)$ periodized time signal $\text{P}\{ x(t)\}$ differs significantly from $x(t)$ due to overlaps.
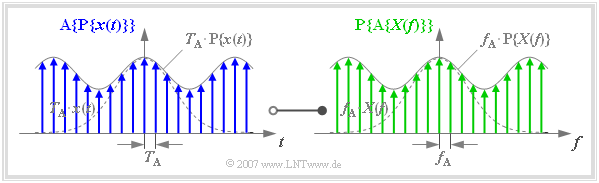
Finite signal representation
One arrives at the so-called »finite signal representation«
- when both the time function $x(t)$ and
- the spectral function $X(f)$
are specified exclusively by their sample values:
The graph is to be interpreted as follows:
- In the left graph the function $\text{A}\{ \text{P}\{ x(t)\}\}$ is drawn in blue. It is obtained by sampling the periodized time function $\text{P}\{ x(t)\}$ with equidistant Dirac delta pulses in the distance $T_{\rm A} = 1/f_{\rm P}$.
- In the right graph the function $\text{P}\{ \text{A}\{ X(f)\}\}$ is drawn in green. This results from periodization $($with $f_{\rm P})$ of the sampled spectral function $\{ \text{A}\{ X(f)\}\}$.
- There is also a Fourier correspondence between the blue finite signal and the green finite signal, as follows:
- $${\rm A}\{{\rm P}\{x(t)\}\} \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} {\rm P}\{{\rm A}\{X(f)\}\} \hspace{0.05cm}.$$
However, the Dirac delta lines of the periodic continuation $\text{P}\{ \text{A}\{ X(f)\}\}$ of the sampled spectral function fall into the same frequency grid as those of $\text{A}\{ X(f)\}$ only if the frequency period $f_{\rm P}$ is an integer multiple $(N)$ of the frequency sampling interval $f_{\rm A}$.
When using the finite signal representation, the following condition must always be fulfilled, where in practice a power of two is usually used for the natural number $N$ $($the graph above is based on the value $N = 8)$:
- $$f_{\rm P} = N \cdot f_{\rm A} \hspace{0.5cm} \Rightarrow\hspace{0.5cm} {1}/{T_{\rm A} }= N \cdot f_{\rm A} \hspace{0.5cm} \Rightarrow\hspace{0.5cm} N \cdot f_{\rm A}\cdot T_{\rm A} = 1\hspace{0.05cm}.$$
If the condition $N \cdot f_{\rm A} \cdot T_{\rm A} = 1$ is satisfied, the order of periodization and sampling can be interchanged. Thus:
- $${\rm A}\{{\rm P}\{x(t)\}\} = {\rm P}\{{\rm A}\{x(t)\}\}\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} {\rm P}\{{\rm A}\{X(f)\}\} = {\rm A}\{{\rm P}\{X(f)\}\}\hspace{0.05cm}.$$
$\text{Conclusions:}$
- The time function $\text{P}\{ \text{A}\{ x(t)\}\}$ has the period $T_{\rm P} = N \cdot T_{\rm A}$.
- The period in the frequency domain is $f_{\rm P} = N \cdot f_{\rm A}$.
- For the description of the discretized time and frequency course $N$ »complex numerical values« in the form of pulse weights are sufficient in each case.
$\text{Example 2:}$ A time-limited $($pulse-like$)$ signal $x(t)$ is present in sampled form, where the distance between two samples is $T_{\rm A} = 1\, {\rm µ s}$:
- After a discrete Fourier transform with $N = 512$ the spectrum $X(f)$ is available as samples with the distance $f_{\rm A} = (N \cdot T_{\rm A})^{–1} \approx 1.953\,\text{kHz} $.
- Increasing the DFT parameter to $N= 2048$ results in a finer frequency grid with $f_{\rm A} \approx 488\,\text{Hz}$.
Discrete Fourier Transform
From the conventional »first Fourier integral«
- $$X(f) =\int_{-\infty }^{+\infty}x(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}t$$
»discretization« $(\text{d}t \to T_{\rm A}$, $t \to \nu \cdot T_{\rm A}$, $f \to \mu \cdot f_{\rm A}$, $T_{\rm A} \cdot f_{\rm A} = 1/N)$ yields the sampled and periodized spectral function
- $${\rm P}\{X(\mu \cdot f_{\rm A})\} = T_{\rm A} \cdot \sum_{\nu = 0 }^{N-1} {\rm P}\{x(\nu \cdot T_{\rm A})\}\cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm} \cdot \hspace{0.05cm}\nu \hspace{0.05cm} \cdot \hspace{0.05cm}\mu /N} \hspace{0.05cm}.$$
It is taken into account that due to the discretization the periodized functions have to be used in each case.
For reasons of a simplified notation we now make the following substitutions:
- Let the $N$ »time-domain coefficients« be associated with the indexing variable $\nu = 0$, ... , $N - 1$:
- $$d(\nu) = {\rm P}\left\{x(t)\right\}{\big|}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A}}\hspace{0.05cm}.$$
- Let the $N$ »frequency-domain coefficients« be associated with the indexing variable $\mu = 0,$ ... , $N$ – 1:
- $$D(\mu) = f_{\rm A} \cdot {\rm P}\left\{X(f)\right\}{\big|}_{f \hspace{0.05cm}= \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm A}}\hspace{0.05cm}.$$
- Abbreviation for the »complex rotation factor« depending on $N$ is written:
- $$w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} = \cos \left( {2 \pi}/{N}\right)-{\rm j} \cdot \sin \left( {2 \pi}/{N}\right) \hspace{0.05cm}.$$
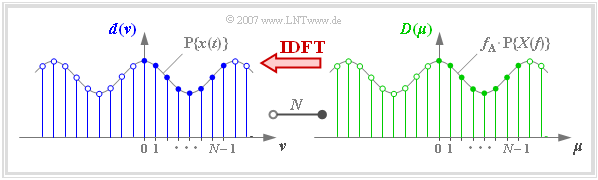
$\text{Definition:}$ The term »Discrete Fourier Transform« $\rm (DFT)$ means the calculation of the $N$ spectral coefficients $D(\mu)$ from the $N$ signal coefficients $d(\nu)$:
- $$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} d(\nu)\cdot {w}^{\hspace{0.05cm}\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}. $$
In the graph you can see in an example
- the $N = 8$ signal coefficients $d(\nu)$ at the blue filling,
- the $N = 8$ spectral coefficients $D(\mu)$ at the green filling.
Inverse Discrete Fourier Transform
The »Inverse Discrete Fourier Transform« describes the »second Fourier integral«:
- $$\begin{align*}x(t) & = \int_{-\infty }^{+\infty}X(f) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm} t}\hspace{0.1cm} {\rm d}f\end{align*}$$
in discretized form:
- $$d(\nu) = {\rm P}\left\{x(t)\right\}{\big|}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A}}\hspace{0.01cm}.$$
$\text{Definition:}$ The term »Inverse Discrete Fourier Transform« $\rm (IDFT)$ refers to the calculation of the signal coefficients $d(\nu)$ from the spectral coefficients $D(\mu)$:
- $$d(\nu) = \sum_{\mu = 0 }^{N-1} D(\mu) \cdot {w}^{-\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$
With the indexing variables
- $\nu = 0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, N-1$,
- $\mu = 0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, N-1$,:
then holds:
- $d(\nu) = {\rm P}\left\{x(t)\right\}{\big \vert}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A} }\hspace{0.01cm},$
- $D(\mu) = f_{\rm A} \cdot {\rm P}\left\{X(f)\right\}{\big \vert}_{f \hspace{0.05cm}= \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm A} } \hspace{0.01cm},$
- $w = {\rm e}^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} \hspace{0.01cm}.$
A comparison between DFT and IDFT shows that exactly the same algorithm can be used. The only differences of the IDFT compared to the DFT are:
- The exponent of the rotation factor must be applied with different sign.
- With the IDFT the division by $N$ is omitted.
Interpretation of DFT and IDFT
The graph shows the discrete coefficients in the time and frequency domain together with the periodized continuous-time functions.
When using DFT or IDFT, it should be noted:
- According to the above definitions, the DFT coefficients $d(ν)$ and $D(\mu)$ always have the unit of the time function.
- Dividing $D(\mu)$ by $f_{\rm A}$ gives the spectral value $X(\mu \cdot f_{\rm A})$.
- The spectral coefficients $D(\mu)$ must always be set complex to be able to consider also odd time functions.
- In order to be able to transform band–pass signals in the equivalent low–pass range, complex time coefficients $d(\nu)$ are usually used.
- The basic interval for $\nu$ and $\mu$ is usually defined as the range from $0$ to $N - 1$, as in the above diagram.
- With the complex-valued number sequences
- $\langle \hspace{0.03cm}d(\nu)\hspace{0.03cm}\rangle = \langle \hspace{0.03cm}d(0), \hspace{0.05cm}\text{...} \hspace{0.05cm} , d(N-1) \hspace{0.03cm}\rangle$,
- $\langle \hspace{0.03cm}D(\mu)\hspace{0.03cm}\rangle = \langle \hspace{0.03cm}D(0), \hspace{0.05cm}\text{...} \hspace{0.05cm} , D(N-1) \hspace{0.03cm}\rangle$:
- ⇒ DFT and IDFT are symbolized similar to the conventional Fourier transform:
- $$\langle \hspace{0.03cm} D(\mu)\hspace{0.03cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.03cm} d(\nu) \hspace{0.03cm}\rangle \hspace{0.05cm}.$$
- If the function $x(t)$ is already limited to the range $0 \le t \lt N \cdot T_{\rm A}$, then the time coefficients output by the IDFT directly indicate the samples of the time function:
- $$d(\nu) = x(\nu \cdot T_{\rm A}).$$
- If $x(t)$ is shifted with respect to the basic interval, one has to choose the assignment between $x(t)$ and the coefficients $d(\nu)$ as shown in $\text{Example 3}$.
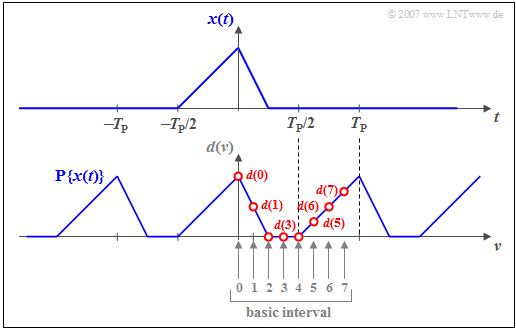
$\text{Example 3:}$ The upper graph shows the asymmetric triangular pulse $x(t)$ whose absolute width is smaller than $T_{\rm P} = N \cdot T_{\rm A}$.
The sketch below shows the assigned DFT coefficients valid for $N = 8$:
- For $\nu = 0,\hspace{0.05cm}\text{...} \hspace{0.05cm} , N/2 = 4$, $d(\nu) = x(\nu \cdot T_{\rm A})$ is valid:
- $$d(0) = x (0)\hspace{0.05cm}, \hspace{0.15cm} d(1) = x (T_{\rm A})\hspace{0.05cm}, \hspace{0.15cm} d(2) = x (2T_{\rm A})\hspace{0.05cm}, $$
- $$d(3) = x (3T_{\rm A})\hspace{0.05cm}, \hspace{0.15cm} d(4) = x (4T_{\rm A})\hspace{0.05cm}.$$
- The coefficients $d(5)$, $d(6)$ and d$(7)$ are to be set as follows:
- $$d(\nu) = x \big ((\nu\hspace{-0.05cm} - \hspace{-0.05cm} N ) \cdot T_{\rm A}\big ) $$
- $$ \Rightarrow \hspace{0.2cm}d(5) = x (-3T_{\rm A})\hspace{0.05cm}, \hspace{0.35cm} d(6) = x (-2T_{\rm A})\hspace{0.05cm}, \hspace{0.35cm} d(7) = x (-T_{\rm A})\hspace{0.05cm}.$$
Exercises
- First select the number $($1, ...$)$ of the exercise.
- A description of the exercise will be displayed.
- The parameter values are adjusted.
- Solution after pressing »Show solution«.
- The number "$0$" corresponds to a »Reset«:
- Same setting as at program start.
- Output of a »reset text« with further explanations about the applet.
(1) New setting: DFT of signal $\rm (b)$: Constant signal. Interpret the result in the frequency domain. What is the analogon of the conventional Fourier transform?
- All coefficients in the time domain are $d(\nu)=1$. Thus all $D(\mu)=0$ with the exception of $\textrm{Re}[D(0)]=1$.
- This corresponds to the conventional $($time-continuous$)$ Fourier Transform: $x(t)=A\hspace{0.15cm} \circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X(f)=A\cdot \delta (f=0)$ with $A=1$.
- All coefficients in the time domain are $d(\nu)=1$. Thus all $D(\mu)=0$ with the exception of $\textrm{Re}[D(0)]=1$.
(2) Assume the obtained $D(\mu)$ field and shift all coefficients one entry down. Which time function does the IDFT provide?
- Now all $D(\mu)=0$, except for $\textrm{Re}[D(1)]=1$. The result in the time domain is a complex exponential function.
- The real part of the $d(\nu)$ field shows a cosine and the imaginary part a sine function. For each function one can see one period respectively.
(3) Add the following coefficient to the current $D(\mu)$ field: $\textrm{Im}[D(1)]=1$. What are the differences compared to (2) in the time domain?
- On the one hand, a phase shift of two support values can now be detected for the real and the imaginary parts. This corresponds to the phase $\varphi = 45^\circ$.
- On the other hand, the amplitudes of the real and the imaginary part were each increased by the factor $\sqrt{2}$.
(4) Set the $D(\mu)$ field to zero except for $\textrm{Re}[D(1)]=1$. Which additional $D(\mu)$ coefficient yields a real $d(\nu)$ field?
- By trial and error, one can see that $\textrm{Re}[D(15)]=1$ must apply additionally. Then the $d(\nu)$ field describes a cosine.
- The following applies to the conventional $($time continuous$)$ Fourier transform: $x(t)=2\cdot \cos(2\pi \cdot f_0 \cdot t)\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X(f)=\delta (f-f_0)+\delta (f+f_0)$.
- The entry $D(1)$ is representative of the frequency $f_0$ and due to the periodicity with $N=16$ the frequency $-f_0$ is expressed by $D(15)=D(-1)$.
(5) According to the IDFT in the $d(\nu)$ field, by which $D(\mu)$ field does one obtain a real cosine function with the amplitude $A=1$?
- Like the conventional Fourier transform the discrete Fourier Transform is linear ⇒ $D(1)=D(15)=0.5$.
(6) New setting: DFT of signal $\rm (e)$: Cosine signal and subsequent signal shifts. What are the effects of these shifts in the frequency domain?
- A shift in the time domain changes the cosine signal to a "harmonic oscillation" with arbitrary phase.
- The $D(\mu)$ field is still zero except for $D(1)$ and $D(15)$. The absolute values $|D(1)|$ and $|D(15)|$ also remain the same.
- The only change concerns the phase, i.e. the different distribution of the absolute values between the real and imaginary part.
(7) New setting: DFT of signal $\rm (f)$: Sinusoidal signal. Interpret the result in the frequency domain. What is the analogon of the conventional Fourier Transform?
- The sine signal results from the cosine signal by applying four time shifts. Therefore all statements of (6) are still valid.
- For the conventional (time continuous) Fourier transform it holds that $x(t)= \sin(2\pi \cdot f_0 \cdot t)\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X(f)=j/2 \cdot [\delta (f+f_0)-\delta (f-f_0)]$.
- The coefficient $D(1)$ $\Rightarrow$ $($frequency: $+f_0)$ is imaginary and has the imaginary part $-0.5$. Accordingly, $\textrm{Im}[D(15)]=+0.5$ ⇒ $($frequency: $-f_0)$ applies.
(8) New setting: DFT of signal $\rm (g)$: Cosine signal (two periods). Interpret the result in comparison to exercise (5).
- Here the time continuous Fourier transform reads $x(t)=\cos(2\pi \cdot (2 f_0) \cdot t)\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X(f)=0.5 \cdot \delta (f- 2 f_0)+0.5 \cdot \delta (f+ 2 f_0)$.
- $D(2)$ is representative of the frequency $2 f_0$. Due to the periodicity, $D(14)=D(-2)$: $D(2)=D(14)=0.5$ is representative of the frequency $-2 f_0$.
(9) Now examine the case DFT of a sinodial signal (two periods). Which modifications do you need to make in the time domain? Interpret the result.
- The desired signal can be obtained from the DFT of signal $\rm (g)$: Cosine signal (two periods) with two shifts. With the result of (7): Four shifts.
- The DFT result is accordingly $\textrm{Im}[D(2)]=-0.5$ and $\textrm{Im}[D(14)]=+0.5$.
(10) New setting: DFT of signal $\rm (h)$: Alternating time coefficients. Interpret the DFT result.
- Here, the time continuous Fourier transform is given by: $x(t)=\cos(2\pi \cdot (8 f_0) \cdot t)\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X(f)=0.5 \cdot \delta (f- 8 f_0)+0.5 \cdot \delta (f+ 8 f_0)$.
- $8 f_0$ is the highest frequency that can be displayed with $N=16$ in the DFT. There are only two sampled values per period, namely $+1$ and $-1$.
- Difference to exercise (5): $D(1)=0.5$ now becomes $D(8)=0.5$. Likewise, $D(15)=0.5$ is shifted to $D(8)=0.5$. Final result: $D(8)=1$.
(11) What are the differences between the two settings DFT from signal $\rm (i)$: Dirac delta impulse and IDFT from spectrum $\rm (I)$: Dirac delta spectrum?
- None! In the first case, all coefficients are $D(\mu)=1$ (real); in the second case, however, equivalently $d(\nu)=1$ (real).
(12) Are there differences in shifting the real "$1$" in the according input fields by one place at a time, that is for $d(\nu = 1)=1$ and $D(\mu = 1)=1$?
- The first case $\Rightarrow$ $\textrm{Re}[d(\nu = 1)]=1$ results in the complex exponential function in the frequency domain given by $X(f)= \textrm{e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2 \pi\hspace{0.05cm}\cdot\hspace{0.05cm} f/f_0}$ with negative sign.
- The second case $\Rightarrow$ $\textrm{Re}[D(\mu = 1)]=1$ results in the complex exponential function in the time domain given by $x(t)= \textrm{e}^{+{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2 \pi\hspace{0.05cm}\cdot\hspace{0.05cm} f_0\cdot t}$ with positive sign.
- Note: With $\textrm{Re}[D(\mu=15)]=1$ the result in the time domain would also be a complex exponential function $x(t)= \textrm{e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2 \pi\hspace{0.05cm}\cdot\hspace{0.05cm} f_0\hspace{0.05cm}\cdot\hspace{0.05cm} t}$ with negative sign.
(13) New setting: DFT of signal $\rm (k)$: Triangle pulse. Interpret the $d(\nu)$ assignment under the assumption $T_\textrm{A} = 1$ ms.
- Change the display to "absolute value". $x(t)$ is symmetrical around $t=0$ and extends from $-8 \cdot T_\textrm{A} = -8$ ms to $+8 \cdot T_\textrm{A}= +8$ ms.
- $d(\nu)$ assignment: $d(0)=x(0)=1$, $d(1)=x(T_\textrm{A})=0.875$, ... , $d(8)=x(8 T_\textrm{A})=0$, $d(9)=x(-7 T_\textrm{A})=0.125$, ... , $d(15)=x(-T_\textrm{A})=0.875$.
(14) Same setting as (13). Interpret the DFT result, especially the coefficients $D(0)$, $D(1)$, $D(2)$ and $D(15)$.
- In the frequency range $D(0)$ stands for the frequency $f=0$ and $D(1)$ and $D(15)$ for the frequencies $\pm f_\textrm{A}$. It holds that $f_\textrm{A}= 1/ (N\cdot T_\textrm{A})=62.5$ Hz.
- For the value of the continuous spectrum at $f=0$ the following applies: $X(f=0)=D(0)/f_\textrm{A} = 0.5/ (0.0625$ kHz$)=8\cdot \textrm{kHz}^{-1}$.
- The first zero of the $\textrm{si}^2$–shaped spectrum $X(f)$ occurs at $2\cdot f_\textrm{A} = 125$ Hz. The other zeros are equidistant.
(15) New setting: DFT of signal $\rm (i)$: Rectangular pulse. Interpret the displayed results.
- The set (symmetrical) rectangle extends over $\pm 4 \cdot T_\textrm{A}$. At the edges, the time coefficients are only half as large: $d(4)=d(12)=0.5$.
- The further statements of (14) also apply to this $\textrm{si}$–shaped spectrum $X(f)$.
(16) Same setting as for (15). Which modifications need to be made in the $d(\nu)$ field, to have the duration of the rectangle $\Rightarrow$ $\pm 2 \cdot T_\textrm{A}$.
- $d(0) = d(1) = d(15) =1, \ d(2) = d(14) = 0.5$. All other time coefficients zero ⇒ first zero of the ${\rm si}$ spectrum at $4 \cdot f_{\rm A}= 250\text{ Hz}$.
(17) New setting: IDFT of spectrum $\rm (L)$: Gaussian spectrum. Interpret the result in the time domain.
- Here, the time function $x(t)$ is Gaussian with the maximum $x(t=0)=4$. For the spectrum the following applies: $X(f=0)=D(0)/f_\textrm{A} = 16 \cdot \textrm{kHz}^{-1}$.
- The equivalent duration of the pulse is $\Delta t = X(f=0)/x(t=0)=4\text{ ms}$. The inverse value gives the equivalent bandwidth $\Delta f = 1/\Delta t = 250\text{ Hz}$.
Applet Manual
(A) Time domain (input and result field)
(B) (A) representation numerical, graphical, magnitude
(C) frequency domain (input and result field)
(D) (C) representation numerical, graphical, magnitude
(E) Selection: DFT $(t \to f)$ or IDFT $(f \to t)$
(F) Given $d(\nu)$ assignments (if DFT), or
Given $D(\mu)$ assignments (if IDFT)
(G) Set input field to zero
(H) Move input field cyclically down (or up)
( I ) Range for experiment execution: exercise selection
(J) Range for experiment execution: exercise definition
(K) Range for experiment execution: show sample solution
- Given $d(\nu)$ assignments (for DFT):
- (a) corresponding number field, (b) DC signal, (c) Complex exponential function of time, (d) Harmonic oscillation $($phase $\varphi = 45^\circ)$,
- (e) Cosine signal (one period), (f) Sine signal (one period), (g) Cosine signal (two periods), (h) Alternating time coefficients,
- (i) Dirac delta pulse, (j) Rectangular pulse, (k) Triangular pulse, (l) Gaussian pulse.
- Given $D(\mu)$ assignments (for IDFT):
- (A) corresponding number field, (B) Constant spectrum, (C) Complex exponential function of frequency, (D) equivalent to setting (d) in time domain ,
- (E) Cosine signal (one frequency period), (F) Sine signal (one frequency period), (G) Cosine signal (two frequency periods), (H) Alternating spectral coefficients,
- (I) Dirac delta spectrum, (J) Rectangular spectrum, (K) Triangular spectrum, (L) Gaussian spectrum.
About the Authors
This interactive calculation tool was designed and implemented at the Institute for Communications Engineering at the Technical University of Munich.
- The first version was created in 2008 by »Thomas Großer« as part of his diploma thesis with “FlashMX – Actionscript” (Supervisor: Günter Söder).
- Last revision and English version 2020/2021 by »Carolin Mirschina« in the context of a working student activity.
The conversion of this applet to HTML 5 was financially supported by Studienzuschüsse ("study grants") of the TUM Faculty EI. We thank them.