Generation of Walsh functions
Open Applet in new Tab Deutsche Version Öffnen
Contents
Program description
This applet allows to display the Hadamard matrices $\mathbf{H}_J$ for the construction of the Walsh functions $w_j$. The factor $J$ of the band spreading as well as the selection of the individual Walsh functions (by means of a blue border around rows of the matrix) can be changed.
Theoretical background
Application
The Walsh functions are a group of periodic orthogonal functions. Their application in digital signal processing mainly lies in the use for band spreading in CDMA systems, for example the mobile radio standard UMTS.
- Due to their orthogonal properties and the favourable periodic cross-correlation function $\rm (PCCF)$, the Walsh functions represent optimal spreading sequences for a distortion-free channel and a synchronous CDMA system. If you take any two lines and form the correlation (averaging over the products), the PCCF value is always zero.
- In asynchronous operation (example: uplink of a mobile radio system) or de-orthogonalization due to multipath propagation, Walsh functions alone are not necessarily suitable for band spreading.
- In terms of $\rm (PACF)$ (periodic autocorrelation function) these sequences are not as good: Each individual Walsh function has a different PACF and each individual PACF is less good than a comparable pseudo noise $\rm (PN)$ sequence. That means: The synchronization is more difficult with Walsh functions than with PN sequences.
Construction
The construction of Walsh functions can be done recursively using the Hadamard matrices.
- A Hadamard matrix $\mathbf{H}_J$ of order $J$ is a $J\times J$ matrix, which contains line by line the $\pm 1$ weights of the Walsh sequences.
- The orders of the Hadamard matrices are fixed to powers of two, i.e. $J = 2^G$ applies to a natural number $G$. Starting from $\mathbf{H}_1 = [+1]$ and
- $$ \mathbf{H}_2 = \left[ \begin{array}{rr} +1 & +1\\ +1 & -1 \\ \end{array}\right] $$
the following relationship applies to the generation of further Hadamard matrices:
- $$ \mathbf{H}_{2N} = \left[ \begin{array}{rr} +\mathbf{H}_N & +\mathbf{H}_N\\ +\mathbf{H}_N & -\mathbf{H}_N \\ \end{array}\right] $$
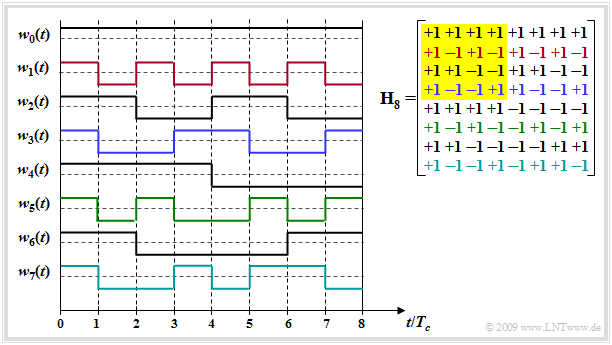
$\text{Example:}$ The graphic shows the Hadamard matrix $\mathbf H_8$ (right) and the $J\hspace{-0.09cm} -\hspace{-0.09cm}1$ spreading sequences which can be constructed with it.
- Only $J\hspace{-0.09cm} -\hspace{-0.09cm}1$, because the unspreaded sequence $w_0(t)$ is usually not used.
- Please note the color assignment between the lines of the Hadamard matrix and the spreading sequences $w_j(t)$.
- The submatrix $\mathbf H_4$ is highlighted in yellow.
How to use the applet
(A) Selection of $G$ ⇒ Band spread factor: $J= 2^G$
(B) Selection of the Walsh function $w_j$ to be marked
About the authors
This interactive calculation tool was designed and realized at the Lehrstuhl für Nachrichtentechnik $\rm (LNT)$ of the Technical University of Munich $\rm (TUM)$.
- The first German version was created in 2007 by Thomas Großer in the context of his diploma thesis with "FlashMX–Actionscript" (Supervisor: Günter Söder).
- 2018/2019 the applet was converted on "HTML5" and redesigned by Carolin Mirschina (Engineering practice, supervisor: Tasnád Kernetzky ).
- 2020 this English version was made by Carolin Mirschina (working student) and Günter Söder.