Period Duration of Periodic Signals

Open Applet in new Tab Deutsche Version Öffnen

Applet Descripition

This applet draws the course and calculates the period duration $T_0$ of the periodic function

$$x(t) = A_1\cdot \cos\left(2\pi f_1\cdot t- \varphi_1\right)+A_2\cdot \cos\left(2\pi f_2\cdot t- \varphi_2\right).$$

Please note:

The phases $\varphi_i$ must be entered here in radians. Conversion from the input value:

$$\varphi_i \text{[in radians]} =\varphi_i \text{[in degrees]}/360 \cdot 2\pi.$$

The maximum value $x_{\rm max}$ and a signal value $x(t_*)$ at a given time $t_*$ are also output.

Theoretical background

A periodic signal $x(t)$ is present exactly when it is not constant and if for all arbitrary values of $t$ and all integer values of $i$ with an appropriate $T_{0}$ applies:

$$x(t+i\cdot T_{0}) = x(t).$$

$T_0$ is called the period duration and $f_0 = 1/T_0$ the basic frequency.

For a harmonic oscillation $x_1(t) = A_1\cdot \cos\left(2\pi f_1\cdot t- \varphi_1\right)$ applies $f_0 = f_1$ and $T_0 = 1/f_1$, independent of the phase $\varphi_1$ and the amplitude $A_1 \ne 0$.

$\text{Calculation Rule: }$ If the periodic signal $x(t)$ consists of two parts $x_1(t)$ and $x_2(t)$ like in this applet, then applies for the basic frequency and the period duration with $A_1 \ne 0$, $f_1 \ne 0$, $A_2 \ne 0$, $f_2 \ne 0$:

$$f_0 = {\rm gcd}(f_1, \ f_2) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}T_0 = 1/f_0.$$

Here $\rm gcd$ denotes the greatest common divisor.

$\text{Examples:}$ In the following $f_0'$, $f_1'$ and $f_2'$ denote signal frequencies normalized to $1\ \rm kHz$:

(a) $f_1' = 1.0$, $f_2' = 3.0$ ⇒ $f_0' = {\rm gcd}(1.0, \ 3.0) = 1.0$ ⇒ $T_0 = 1.0\ \rm ms$;

(b) $f_1' = 1.0$, $f_2' = 3.5$ ⇒ $f_0' = {\rm gcd}(1.0, \ 3.5)= 0.5$ ⇒ $T_0 = 2.0\ \rm ms$;

(c) $f_1' = 1.0$, $f_2' = 2.5$ ⇒ $f_0' = {\rm gcd}(1.0, \ 2.5) = 0.5$ ⇒ $T_0 = 2.0\ \rm ms$;

(d) $f_1' = 0.9$, $f_2' = 2.5$ ⇒ $f_0' = {\rm gcd}(0.9, \ 2.5) = 0.1$ ⇒ $T_0 = 10.0 \ \rm ms$;

(e) $f_2' = \sqrt{2} \cdot f_1' $ ⇒ $f_0' = {\rm gcd}(f_1', \ f_2') \to 0$ ⇒ $T_0 \to \infty$ ⇒ the signal $x(t)$ is not periodic.

$\text{Note:}$ The period duration could also be determined as least common multiple $\rm (lcm)$ according to $T_0 = {\rm lcm}(T_1, \ T_2)$:

(c) $T_1 = 1.0\ \rm ms$, $T_2 = 0.4\ \rm kHz$ ⇒ $T_0 = {\rm lcm}(1.0, \ 0.4) \ \rm ms = 2.0\ \rm ms$

With all other parameter values, however, there would be numerical problems, for example

(a) $T_1 = 1.0\ \rm ms$ and $T_2 = 0.333\text{...} \ \rm ms$ have no "least common multiple" due to the limited representation of real numbers.

Exercises

First select the number (1, 2, ... ) of the exercise. The number 0 corresponds to a "Reset": Same setting as at the program start.
An exercise description is displayed. Parameter values are adjusted. Solution after pressing "Show solution".
$A_1'$ and $A_2'$ denote the signal amplitudes normalized to $1\ \rm V$. $f_0'$, $f_1'$ and $f_2'$ are the frequencies normalized to $1\ \rm kHz$.

(1) Consider $A_1' = 1.0, \ A_2' = 0.5, \ f_1' = 2.0, \ f_2' = 2.5, \ \varphi_1 = 0^\circ \ \varphi_2 = 90^\circ$. How large is the period $T_0$?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$The period is $T_0 = 2.0 \ \rm ms$ due to $\rm{gcd}(2.0, 2.5) = 0.5$.

(2) Vary $\varphi_1$ and $\varphi_2$ in the whole possible range $\pm 180^\circ$. How does this affect the period $T_0$?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$The period $T_0 = 2.0 \ \rm ms$ remains the same for all $\varphi_1$ and $\varphi_2$.

(3) Select the default setting ⇒ "Recall Parameters". Vary $A_1'$ in the entire possible range $0 \le A_1' \le 1$.

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$The period $T_0 = 2.0 \ \rm ms$ remains the same with the exception of $A_1' =0$. In the latter case: $T_0 = 0.4 \ \rm ms$.

(4) Choose the default setting ⇒ "Recall Parameters" and vary $f_2'$. Does this affect $T_0$? Which value is the result for $f_2' = 0.2$?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$The period jumps back and forth. For $f_2' = 0.2$ the result is $T_0 = 5.0 \ \rm ms$ because of $\ \rm{gcd} (2.0,0.2)=0.2$.

(5) Consider $A_1' = 1.0, \ A_2' = 0.5, \ f_1' = 0.2, \ f_2' = 2.5, \ \varphi_1 = 0^\circ \ \varphi_2 = 90^\circ$. How large is the period $T_0$? Save this setting with "Store Parameters".

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$The period is $T_0 = 10.0 \ \rm ms$ due to $\rm{gcd}(0.2, 2.5) = 0.1$.

(6) Select the last setting ⇒ "Recall Parameters" and change $f_2' = 0.6$. Save this setting with "Store Parameters".

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$The period is $T_0 = 5.0 \ \rm ms$ due to $\rm{gcd}(0.2,0.6) = 0.2$.

(7) How large is the maximum signal value $x_{\rm max}$ with the same settings?`

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$ $x_{\rm max} =x(t_* + i \cdot T_0) = 1.38 \ {\rm V} < A_1 + A_2$ with $t_* = 0.3 \ \rm ms$ and $T_0 = 5.0 \ \rm ms$.

(8) What changes with $\varphi_2 = 0^\circ$ ⇒ Sum of two cosine waves?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$ $t_* = 0$, $T_0 = 5.0 \ \rm ms$ ⇒ $x_{\rm max} =x(t_* + i \cdot T_0) = 1.5 \ {\rm V}=A_1 + A_2$.

(9) Now consider $\varphi_1 = \varphi_2 = 90^\circ$ ⇒ Sum of two sine waves?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$The maximum signal value is now $x_{\rm{max}} = 1.07 \ \rm V < A_1 + A_2$. This value results from $T_0 = 5.0 \ \rm ms$ and $t_* = 0.6 \ \rm ms$ or $t_* = 1.9 \ \rm ms$.

Applet Manual

Screenshot

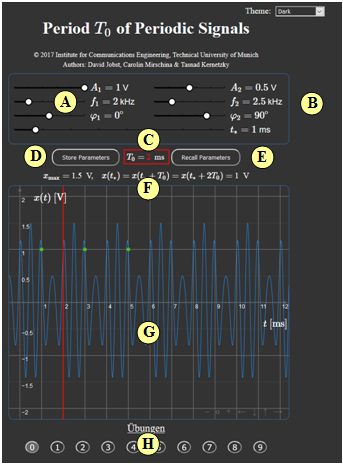
(A) Parameter input for harmonic oscillation 1

(B) Parameter input for harmonic oscillation 2 and time $t_*$.

(C) Numerical output of the main result $T_0$; graphical illustration by red line

(D) Save parameter sets

(E) Retrieve parameter sets

(F) Output of $x_{\rm max}$ and the signal values $x(t_*) = x(t_* + T_0)= x(t_* + 2T_0)$

(G) Graphic field for displaying the signals

The signal values $x(t_*) = x(t_* + T_0)= x(t_* + 2T_0)$ are marked by green dots

At the bottom of the graphic field you will find the following buttons:

(1) Zoom funktions: "$+$" (Zoom In), "$-$" (Zoom Out), $\rm o$ (Reset)

(2) Move with "←" (Section to the left, ordinate to the right), "$\uparrow$" "$\downarrow$", "$\rightarrow$"

(H) Task selection according to the task number

In all applets top right: Changeable graphical interface design ⇒ Theme:

Dark: black background (recommended by the authors).
Bright: white background (recommended for beamers and printouts)
Deuteranopia: for users with pronounced green–visual impairment
Protanopia: for users with pronounced red–visual impairment

About the Authors

This interactive calculation tool was designed and implemented at the Institute for Communications Engineering at the Technical University of Munich.

The first German version was created in 2004 by Ji Li as part of her diploma thesis with “FlashMX – Actionscript” (Supervisor: Günter Söder).
In 2017 the program was redesigned by David Jobst (Bachelor thesis LB, Supervisor: Tasnád Kernetzky ) via "HTML5".
The English version was done in 2020 by Carolin Mirschina.

Once again: Open Applet in new Tab