Exercise 1.07: Check and Generator Matrix of the HC (7, 4, 3)

Parity-check equations of the
$(7, 4, 3)$ Hamming code

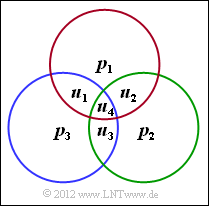
The graph shows the parity-check equations of the $(7, 4, 3)$ Hamming code, which has already been considered in detail in the "Exercise 1.6" and described using the code table.

In this task, this code is now characterized by two matrices – as is common in Channel Coding:

The parity-check matrix $\boldsymbol{\rm H}$ is a matrix with $m = n - k$ rows and $n$ columns. It describes the $m = 3$ parity-check equations, where the first row refers to the elements of the red circle and the second row refers to those of the green circle. The last row gives the modulo-2 sum of the blue circle.

A second description possibility is provided by the generator matrix $ \boldsymbol{\rm G}$ with $k$ rows and $n$ columns. It gives the relationship between the information words $ \underline{u}$ and the code words $\underline{x}$ :

$$ \underline{x} = \underline{u} \cdot { \boldsymbol{\rm G}} \hspace{0.05cm}.$$

From this and from the equation $ \boldsymbol{\rm H} · \underline{x}^{\rm T} = \underline{0}$ the relation between the parity-check matrix $ \boldsymbol{\rm H}$ and the generator matrix $ \boldsymbol{\rm G}$ can be established:

$$\underline{x}^{\rm T} = { \boldsymbol{\rm G}}^{\rm T} \cdot \underline{u}^{\rm T} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} { \boldsymbol{\rm H}} \cdot { \boldsymbol{\rm G}}^{\rm T} \cdot \underline{u}^{\rm T} = \underline{0}\hspace{0.5cm} \forall \hspace{0.15cm}\underline{u} \in {\rm GF}(2^k)\hspace{0.3cm} \Rightarrow \hspace{0.3cm} { \boldsymbol{\rm H}} \cdot { \boldsymbol{\rm G}}^{\rm T} = { \boldsymbol{\rm 0}} \hspace{0.05cm}.$$

Note that in these equations "$\underline{0}$" denotes a row vector with $k$ elements and "$\boldsymbol{\rm 0}$" denotes a matrix with $m$ rows and $k$ columns. All elements of "$\underline{0}$" or "$\boldsymbol{\rm 0}"$ are zero.

If the code is a systematic code, the description variables $\boldsymbol{\rm H}$ and $\boldsymbol{\rm G}$ can be written with the aid of identity matrices $\boldsymbol{\rm I}$ as follows:

$${ \boldsymbol{\rm G}} =\left({ \boldsymbol{\rm I}}_k \: ; \: { \boldsymbol{\rm P}}\right) \hspace{0.5cm} \Rightarrow \hspace{0.5cm} { \boldsymbol{\rm H}} = \left({ \boldsymbol{\rm P}}^{\rm T}\: ; \:{ \boldsymbol{\rm I}}_m \right) \hspace{0.05cm}.$$

$\boldsymbol{\rm P}$ is thereby a matrix with $k$ rows and $m$ columns. Accordingly, the transposed matrix ${ \boldsymbol{\rm P}}^{\rm T}$ consists of $m$ rows and $k$ columns.

Hints :

This exercise belongs to the chapter "General Description of Linear Block Codes".

Reference is made in particular to the sections "Code definition by the parity-check matrix" and "Code definition by the generator matrix".

Questions

Solution

(1) The number of columns of the parity-check matrix $\boldsymbol{\rm H}$ is equal to the code length $\underline{n = 7}$.

The number of rows is equal to the number of parity-check equations, in this case $\underline{m = 3} = n - k$.

(2) A comparison with the graph in the information section shows that all statements are true. With

$$\underline{x} = ( x_1, x_2, x_3, x_4, x_5, x_6, x_7) = ( u_1, u_2, u_3, u_4, p_1, p_2, p_3)$$

results in the following parity-check equations:

$$x_1 \oplus x_2 \oplus x_4 \oplus x_5 \hspace{-0.1cm}\ = \ \hspace{-0.1cm} 0 \hspace{0.3cm}{\rm (red\hspace{0.15cm}circle)}\hspace{0.05cm},$$

$$x_2 \oplus x_3 \oplus x_4 \oplus x_6 \hspace{-0.1cm}\ = \ \hspace{-0.1cm} 0 \hspace{0.3cm}{\rm (green\hspace{0.15cm}circle)}\hspace{0.05cm},$$

$$ x_1 \oplus x_3 \oplus x_4 \oplus x_7 \hspace{-0.1cm}\ = \ \hspace{-0.1cm} 0 \hspace{0.3cm}{\rm (blue\hspace{0.15cm}circle)}\hspace{0.05cm}.$$

This gives for the parity-check matrix:

$${ \boldsymbol{\rm H}} = \begin{pmatrix} 1 &1 &0 &1 &1 &0 &0\\ 0 &1 &1 &1 &0 &1 &0\\ 1 &0 &1 &1 &0 &0 &1 \end{pmatrix}\hspace{0.05cm}.$$

The specification of $\boldsymbol{\rm H}$ is not unique. A different order of the parity-check equations would, for example, result in a second parity-check matrix which is also correct:

$${ \boldsymbol{\rm H}}' = \begin{pmatrix} 1 &0 &1 &1 &0 &0 &1\\ 1 &1 &0 &1 &1 &0 &0\\ 0 &1 &1 &1 &0 &1 &0 \end{pmatrix}\hspace{0.05cm}.$$

(3) Statement 2 is correct:

For a systematic code, the parity-check matrix can be represented in the following form:

$${ \boldsymbol{\rm H}} =\left({ \boldsymbol{\rm P}}^{\rm T}\: ; \:{ \boldsymbol{\rm I}}_m \right) \hspace{0.05cm}.$$

In the present example, with $m = 3$:

$${ \boldsymbol{\rm P}}^{\rm T} = \begin{pmatrix} 1 &1 &0 &1\\ 0 &1 &1 &1\\ 1 &0 &1 &1 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm I}}_3 = \begin{pmatrix} 1 &0 &0\\ 0 &1 &0\\ 0 &0 &1 \end{pmatrix}\hspace{0.05cm}.$$

(4) Statement 1 and 3 are correct:

In general, the relationship between the $m×n$ parity-check matrix and the $k×n$ generator matrix is:

$${ \boldsymbol{\rm H}} \cdot { \boldsymbol{\rm G}}^{\rm T} = { \boldsymbol{\rm 0}} \hspace{0.05cm}$$

The matrix "$ \boldsymbol{\rm 0}$" is filled with zeros only and has $m$ rows and $k$ columns. For a systematic code – like here – the following relation exists:

$${ \boldsymbol{\rm H}} =\left({ \boldsymbol{\rm P}}^{\rm T}\: ; \:{ \boldsymbol{\rm I}}_m \right) \hspace{0.3cm}\Leftrightarrow \hspace{0.3cm}{ \boldsymbol{\rm G}} =\left({ \boldsymbol{\rm I}}_k \: ; \:{ \boldsymbol{\rm P}} \right) \hspace{0.05cm}.$$

In the present case, one obtains:

$${ \boldsymbol{\rm I}}_4 = \begin{pmatrix} 1 &0 &0 &0\\ 0 &1 &0 &0\\ 0 &0 &1 &0\\ 0 &0 &0 &1 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm P}} = \begin{pmatrix} 1 &0 &1\\ 1 &1 &0\\ 0 &1 &1\\ 1 &1 &1 \end{pmatrix}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} { \boldsymbol{\rm G}} = \begin{pmatrix} 1 &0 &0 &0 &1 &0 &1\\ 0 &1 &0 &0 &1 &1 &0\\ 0 &0 &1 &0 &0 &1 &1\\ 0 &0 &0 &1 &1 &1 &1 \end{pmatrix}\hspace{0.05cm}.$$

(5) The equation to be used is:

$$\underline{x}_{11} \hspace{-0.15cm}\ = \ \hspace{-0.15cm} \underline{u}_{11} \cdot { \boldsymbol{\rm G}} = \begin{pmatrix} 1 &0 &1 &1 \end{pmatrix} \cdot \begin{pmatrix} 1 &0 &0 &0 &1 &0 &1\\ 0 &1 &0 &0 &1 &1 &0\\ 0 &0 &1 &0 &0 &1 &1\\ 0 &0 &0 &1 &1 &1 &1 \end{pmatrix} = \begin{pmatrix} 1 &0 &1 &1 &0 &0 &1 \end{pmatrix}\hspace{0.05cm}.$$

A comparison with the table of "Exercise 1.6" shows the correctness of this calculation ⇒ Answer 3.

The answer 1 cannot be correct already because this does not correspond to any systematic coding.
(1, 0, 1, 1, 0, 0) according to suggestion 2 is not a valid code word. Hereby the blue parity-check equation in the graphic in the information section is not fulfilled.

	The first row is: $(1101100)$.
	The second row is: $(0111010)$.
	The third row is: $(1011001)$.

	In each row there is an even number of ones.
	At the end of $\boldsymbol{\rm H}$ you can recognize an identity matrix.
	The middle column of $\boldsymbol{\rm H}$ is occupied by ones.

	The first row is: $(1000101)$,
	The second row is: $(0111010)$,
	The last row is: $(0001111)$.

	$x_{11} = (1, 1, 1, 1, 0, 0, 0),$
	$x_{11} = (1, 0, 1, 1, 0, 0, 0),$
	$x_{11} = (1, 0, 1, 1, 0, 0, 1).$