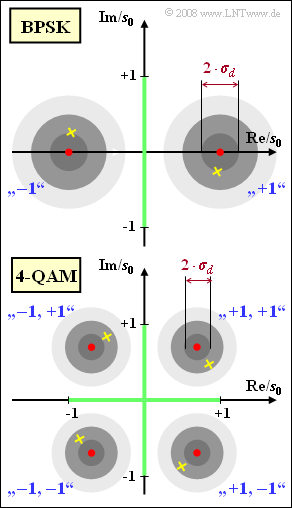
The diagram shows schematically the phase diagrams of the "binary phase modulation" $($abbreviated $\rm BPSK)$ and the "quadrature amplitude modulation" $($called $\rm 4–QAM)$.
- The latter can be described by two BPSK systems with cosine and minus-sine carriers, where for each of the subcomponents the transmission amplitude is reduced by a factor of $\sqrt{2}$ compared to BPSK.
- The envelope of the total signal $s(t)$ is thus also constant equal to $s_{0}$.
- The error probability depending on the quotient $E_{\rm B}/N_{0}$ is the same for BPSK and 4–QAM:
- $$p_{\rm B} = \ {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = \ {1}/{2}\cdot {\rm erfc}\left ( \sqrt{E_{\rm B}/{ N_0 }} \right ).$$
However, the error probability of the BPSK system can also be expressed in the form
- $$p_{\rm B,\hspace{0.04cm}BPSK} = {\rm Q}\left ( \frac{s_0}{\sigma_d } \right )\hspace{0.2cm}{\rm with}\hspace{0.2cm}\sigma_d = \sqrt{\frac{N_0}{T_{\rm B}}}$$
Correspondingly, for the 4-QAM system:
- $$p_{\rm B,\hspace{0.04cm}QAM} = {\rm Q}\left ( \frac{s_0/\sqrt{2}}{\sigma_d } \right )\hspace{0.2cm}{\rm with}\hspace{0.2cm}\sigma_d = \sqrt{\frac{N_0}{2 \cdot T_{\rm B}}}.$$
The equations are valid only under the condition of exact phase synchronization:
- If there is a phase offset $\Delta\phi_{\rm T}$ between the transmitted and received carrier signals, the error probability increases significantly, with BPSK and QAM systems being degraded differently.
- In the phase diagram, the phase offset is noticeable by a rotation of the point clouds.
- In the diagram, the centers of the point clouds for $\Delta\phi_{\rm T} = 15^\circ$ are marked by yellow crosses, while the red circles indicate the centers for $\Delta\phi_{\rm T} = 0$.
$E_{\rm B}/N_{0} = 8$ always holds, so the error probabilities of BPSK and QAM in the best case (without phase shift) are as follows ⇒ "Exercise 1.8Z":
- $$p_{\rm B} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {\rm Q}(4)= 0.317 \cdot 10^{-4}.$$
Further remarks:
- If we denote the distance of the BPSK useful samples (without noise) from the (vertical) decision threshold by $s_{0}$, we get $\sigma_{d} = s_{0}/4$ for the noise rms value. The lighter circles in the diagram mark the contour lines with radius $2\cdot \sigma_{d}$ and $3\cdot \sigma_{d}$ of the two-dimensional Gaussian PDF.
- For the 4-QAM, compared to the BPSK, the distances of the noise-free samples drawn in red from the now two decision thresholds are each smaller by a factor of $\sqrt{2}$, but it also results in a noise rms value $\sigma_{d}$ smaller by the same factor.
Notes:
- The exercise belongs to the chapter "Linear Digital Modulation - Coherent Demodulation".
- Reference is made in particular to the section "Phase offset between transmitter and receiver".
- You can determine the values of the Q–function with the HTML5/JavaScript applet "Complementary Gaussian Error Functions".
Questions
Solution
(1) Rotating the phase diagram by $\Delta\phi_{\rm T} = 15^\circ$ decreases the distance of the useful samples from the threshold by $\cos(15^\circ) \approx 0.966$. It follows that:
- $$p_{\rm B} = {\rm Q}(0.966 \cdot 4) \approx {\rm Q}(3.86)= 0.57 \cdot 10^{-4}\hspace{0.1cm}\underline {= 0.0057\, \%}.$$
(2) Analogous to subtask (1), $\cos(45^\circ) \approx 0.707$ is obtained:
- $$p_{\rm B} = {\rm Q}(0.707 \cdot 4) \approx {\rm Q}(2.83)\hspace{0.1cm}\underline {= 0.233 \, \%}.$$
(3) For 4-QAM, clockwise rotation by $\Delta\phi_{\rm T}$ increases the distance
- from the horizontal threshold (decision of the first bit) equals $s_{0} \cdot \cos(45^\circ + \Delta\phi_{\rm T})$, i.e., smaller than without phase shift,
- from the vertical threshold (decision of the second bit) equal to $s_{0} \cdot \cos(45^\circ - \Delta\phi_{\rm T})$, thus larger than without phase shift.
Thus, we obtain for the average error probability:
- $$p_{\rm B} = {1}/{2} \cdot {\rm Q}\left ( \frac{\cos(45^\circ+{\rm \Delta} \phi_{\rm T}) \cdot s_0}{0.25 \cdot s_0 / \sqrt{2}} \right ) + {1}/{2} \cdot {\rm Q}\left ( \frac{\cos(45^\circ-{\rm \Delta} \phi_{\rm T}) \cdot s_0}{0.25 \cdot s_0 / \sqrt{2}}\right ).$$
- This already takes into account the smaller noise rms value of the 4-QAM.
- As a check, we calculate the error probability for $\Delta\phi_{\rm T} = 0$:
- $$p_{\rm B} = {1}/{2} \cdot {\rm Q}\left ( \frac{\cos(45^\circ) \cdot 4}{1 / \sqrt{2}} \right ) +{1}/{2} \cdot {\rm Q}\left ( \frac{\cos(45^\circ) \cdot 4}{1 / \sqrt{2}} \right )= {\rm Q}(4) = 0.317 \cdot 10^{-4}.$$
- On the other hand, we obtain with $\Delta\phi_{\rm T} = 15^\circ$:
- $$p_{\rm B} = {1}/{2} \cdot {\rm Q}\left ( \frac{\cos(60^\circ) \cdot 4}{1 / \sqrt{2}} \right ) +{1}/{2} \cdot {\rm Q}\left ( \frac{\cos(30^\circ) \cdot 4}{1 / \sqrt{2}} \right )= {1}/{2} \cdot \left [{\rm Q}(2.83)+ {\rm Q}(4.90)\right]$$
- $$\Rightarrow \hspace{0.3cm} p_{\rm B} \approx \frac{1}{2} \cdot \left [0.233 \cdot 10^{-2}+ 0.479 \cdot 10^{-6}\right] \hspace{0.1cm}\underline {= 0.117 \, \%}.$$
(4) With a phase shift of $45^\circ$, one obtains from the equation generally derived above:
- $$p_{\rm B} ={1}/{2} \cdot {\rm Q}\left ( \frac{\cos(90^\circ) \cdot 4}{1 / \sqrt{2}} \right ) +{1}/{2} \cdot {\rm Q}\left ( \frac{\cos(0^\circ) \cdot 4}{1 / \sqrt{2}} \right )= {1}/{2} \cdot \left [{\rm Q}(0)+ {\rm Q}(5.66)\right] \approx 0.25\hspace{0.1cm}\underline {= 25 \, \%}.$$
That is:
- The bit error rate for the first bit is $50\%$.
- In contrast, the second bit is decided almost error-free $(\approx 10^{–8})$.
- Overall, this results in a mean bit error probability of approx. $25\%$.