Exercise 1.1: Basic Transmission Pulses

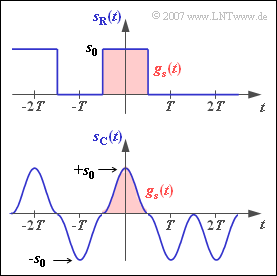
Considered basic transmission pulses

In this exercise, we examine the two transmitted signals $s_{\rm R}(t)$ and $s_{\rm C}(t)$ with rectangular resp. cosine–square basic transmission pulse, shown in the diagram.

In particular, the following characteristics are to be calculated for the respective basic transmission pulses $g_s(t)$:

the equivalent pulse duration of $g_s(t)$:

$$\Delta t_{\rm S} = \frac {\int ^{+\infty} _{-\infty} \hspace{0.15cm} g_s(t)\,{\rm d}t}{{\rm Max} \hspace{0.05cm}[g_s(t)]} \hspace{0.05cm},$$

the energy of $g_s(t)$:

$$E_g = \int^{+\infty} _{-\infty} g_s^2(t)\,{\rm d}t \hspace{0.05cm},$$

the power of the transmitted signal $s(t)$:

$$P_{\rm S} = \lim_{T_{\rm M} \to \infty} \frac{1}{+T_{\rm M}} \cdot \int^{+T_{\rm M}/2} _{-T_{\rm M}/2} s^2(t)\,{\rm d}t \hspace{0.05cm}.$$

Always assume in your calculations that the two possible amplitude coefficients are equally likely and that the distance between adjacent symbols is $T = 1 \ \rm µ s$. This corresponds to a bit rate of $R = 1 \ \rm Mbit/s$.

The (positive) maximum value of the transmitted signal is the same in both cases:

$$s_0 = \sqrt{0.5\, {\rm W}} \hspace{0.05cm}.$$

Assuming that the transmitter is terminated with a $50\ \rm Ω$ resistor, this corresponds to the following voltage value:

$$s_0^2 = 0.5\, {\rm W} \cdot 50\, {\rm \Omega} = 25\, {\rm V}^2 \hspace{0.15cm} \Rightarrow \hspace{0.15cm} s_0 =5\, {\rm V} \hspace{0.05cm}.$$

Notes:

The exercise belongs to the chapter "System Components of a Baseband Transmission System".
Reference is made in particular to the section "Characteristics of the digital transmitter".
Given is the following indefinite integral:

$$\int \cos^4(a x)\,{\rm d}x = \frac{3}{8} \cdot x + \frac{1}{4a} \cdot \sin(2 a x)+ \frac{1}{32a} \cdot \sin(4 a x)\hspace{0.05cm}.$$

Questions

	$s_{\rm R}(t)$ is a bipolar signal and $s_{\rm C}(t)$ is a unipolar signal.
	$s_{\rm C}(t)$ is a bipolar signal and $s_{\rm R}(t)$ is a unipolar signal.

$\text{For the signal}\ \ s_{\rm R}(t) \text{:} \ \ \Delta t_{\rm S}/T \ = \ $

$\text{For the signal}\ \ s_{\rm C}(t) \text{:} \ \ \Delta t_{\rm S}/T \ = \ $

$E_g \ = \ $

$\ \cdot 10^{-6}\ \rm Ws$

$P_{\rm S} \ = \ $

$\ \rm W$

$E_g \ = \ $

$\ \cdot 10^{-6}\ \rm Ws$

$P_{\rm S} \ = \ $

$\ \rm W$

Solution

(1) Solution 2 is correct:

In both cases, the transmitted signal can be represented in the following form:

$$s(t) = \sum_{(\nu)} a_\nu \cdot g_s ( t - \nu \cdot T)$$

For the signal $s_{\rm R}(t)$, the amplitude coefficients $a_ν$ are either $0$ or $1$. Thus, a unipolar signal is present.
In contrast, for the bipolar signal $s_{\rm R}(t)$ ⇒ $a_ν ∈ \{–1, +1\}$ holds.

(2) The signal $s_{\rm R}(t)$ is NRZ ("non-return-to-zero") rectangular.

Accordingly, both the absolute pulse duration $T_{\rm S}$ and the equivalent pulse duration $\Delta t_{\rm S}$ are equal to the symbol duration $T$:

$$T_{\rm S} / T = 1\hspace{0.05cm},\hspace{0.3cm}\Delta t_{\rm S} / T \hspace{0.1cm}\underline{ = 1 }\hspace{0.05cm}.$$

The basic transmission pulse for the signal $s_{\rm C}(t)$ is:

$$g_s(t) = \left\{ \begin{array}{c} s_0 \cdot \cos^2(\pi \cdot \frac{t}{T}) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{for}} \\ \\ \end{array}\begin{array}{*{20}c} -T/2 \le t \le +T/2 \hspace{0.05cm}, \\ {\rm else} \hspace{0.05cm}. \\ \end{array}$$

From the diagram on the information section, we can see that the following values apply to the cosine–square pulse:

$$T_{\rm S} / T = 1\hspace{0.05cm},\hspace{0.3cm}\Delta t_{\rm S} / T \hspace{0.1cm}\underline{ = 0.5} \hspace{0.05cm}.$$

(3) For the energy of the rectangular pulse holds:

$$E_g = \int^{+\infty} _{-\infty} g_s^2(t)\,{\rm d}t = s_0^2 \cdot T = 0.5\, {\rm W} \cdot 1\, {\rm µ s} \hspace{0.1cm}\underline{= 0.5 \cdot 10^{-6}\, {\rm Ws}}\hspace{0.05cm}.$$

(4) For a bipolar rectangular signal, the following would apply:

$$s_{\rm R}^2(t)= s_0^2 = {\rm const.} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} P_s = s_0^2 \cdot \lim_{T_{\rm M} \to \infty} \frac{1}{T_{\rm M}} \cdot \int ^{T_{\rm M}/2} _{-T_{\rm M}/2} \,{\rm d}t = s_0^2 \hspace{0.05cm}.$$

However, since the signal $s_{\rm R}(t)$ is unipolar here, in half the time $s_{\rm R}(t)= 0$. Thus, we get:

$$P_{\rm S} = {1}/{2} \cdot s_0^2 \hspace{0.1cm}\underline{= 0.25 \,{\rm W}} \hspace{0.05cm}.$$

(5) For the energy of the cosine–square pulse holds:

$$E_g = \int^{+\infty} _{-\infty} g_s^2(t)\,{\rm d}t = 2 \cdot s_0^2 \cdot \int^{T/2} _{0} \cos^4(\pi \cdot {t}/{T})\,{\rm d}t \hspace{0.05cm}.$$

Here, the formula derived in subtask (3) and the symmetry of $g_s(t)$ about time $t = 0$ are considered.
The integral is given in the task description, where $a = π/T$ is to be set:

$$E_g = 2 \cdot s_0^2 \cdot \left [ \frac{3}{8} \cdot t + \frac{T}{4\pi} \cdot \sin(2 \pi \frac{t}{T})+ \frac{T}{32\pi} \cdot \sin(4 \pi \frac{t}{T})\right ]_{0}^{T/2}\hspace{0.05cm}.$$

The lower bound $t = 0$ always yields the result $0$. With respect to the upper bound, only the first term yields a result different from $0$. Thus:

$$E_g = 2 \cdot s_0^2 \cdot \frac{3}{8} \cdot \frac{T}{2} = \frac{3}{8} \cdot 5 \cdot 10^{-7}\, {\rm Ws} \hspace{0.1cm}\underline{ = 0.1875 \cdot 10^{-6}\, {\rm Ws}}\hspace{0.05cm}.$$

(6) The following relationship holds for the bipolar signal $s_{\rm C}(t)$:

$$P_{\rm S} = \frac{ E_g}{T} = \frac{ 1.875 \cdot 10^{-7}\, {\rm Ws}}{10^{-6}\, {\rm s}}\hspace{0.1cm}\underline{ = 0.1875 \,{\rm W}} \hspace{0.05cm}.$$