Exercise 1.2Z: Three-dimensional Representation of Codes

Space $\rm GF(2^3)$ and
code of length $n = 3$

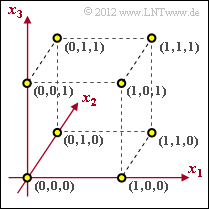
Codes for error detection or error correction can be represented very clearly in an $n$-dimensional space. We restrict ourselves here to binary codes of length $n = 3$:

$$\underline{x} = (x_{1},\ x_{2},\ x_{3}) \hspace{0.1cm} \in \hspace{0.1cm}{\rm GF}(2^3) \hspace{0.05cm},\hspace{0.5cm} x_i = \{0,\ 1 \}\hspace{0.05cm},\hspace{0.2cm} i = 1, 2, 3\hspace{0.05cm}.$$

In general, for block coding:

The information word $\underline{u} = (u_{1},\ u_{2}, \ \text{...} , \ u_{k})$ is uniquely transformed into the code word $\underline{x} =(x_{1},\ x_{2}, \ \text{...} , \ , x_{n})$.

The code rate is $R = k/n$.

The Hamming distance $d_{\rm H}(x, \hspace{0.05cm}x\hspace{0.05cm}')$ between two code words $x ∈ \mathcal{C}$ and $x\hspace{0.05cm}' ∈ \mathcal{C}$ indicates the number of bit positions in which $x$ and $x\hspace{0.05cm}'$ differ.

The minimum distance $d_{\rm min} = {\rm min}\big[d_{\rm H}(x, \hspace{0.05cm}x\hspace{0.05cm}')\big]$ is a measure of the correctability of a code.

It can detect $e =d_{\rm min} - 1$ errors and can correct $t =(d_{\rm min} - 1)/2$ errors.

The last statement, however, is valid only for odd $d_{\rm min}$.

Hints:

This exercise belongs to the chapter "Objective of Channel Coding"

In addition, some simple questions about the chapter "Examples of binary block codes" are anticipated.

Questions

Solution

(1) Correct statements 1 and 3:

In this assignment, $k = 3$ information bits are mapped to $n = 3$ code bits ⇒ $R = k/n = 1$.
The statement $\underline{x} = \underline{u} $ would only hold in the case of systematic coding.
For example, in principle. $(0, 0, 0)$ → $(0, 1, 1)$ would also be possible.
The last statement is certainly false: From the graph one can see the minimum distance $d_{\rm min} = 1$.

Two $(3, 2, 2)$ block codes

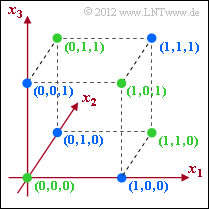
(2) Correct statements 1 and 2:

$\mathcal{C}_{1}$ and $\mathcal{C}_{2}$ actually describe codes with rate $R = 2/3$ and minimum distance $d_{\rm min} = 2$.
In the graph, the green dots mark the code $\mathcal{C}_{1}$ and the blue dots mark the code $\mathcal{C}_{2}$.
For the code $\mathcal{C}_{3}$ – also with rate $R = 2/3$ – the minimum distance between two code words is $d_{\rm min} = 1$,
for example between $(0, 0, 0)$ and $(1, 0, 0)$ or between $(0, 1, 1)$ and $(1, 1, 1)$.

(3) Correct is only statement 1:

Only a bit error can be detected with the minimum distance $d_{\rm min} = 2$.
In the upper graph, the green dots indicate allowed code words of $\mathcal{C}_{1}$.
If a blue dot is received, this indicates a transmission error.
On the other hand, error correction is not possible with $d_{\rm min} = 2$.
The code $\mathcal{C}_{1}$ corresponds to the single parity-check code $(3, 2, 2)$.

$(3, 1, 3)$ block code

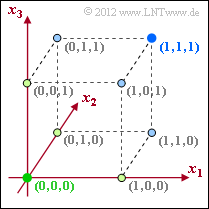
(4) Correct answers 2, 3, and 4:

$C_{4}$ describes the $(3, 1, 3)$ repetition code. In this code, two of the total eight possible points are occupied, from which one could incorrectly conclude the code rate $R = 1/4$.
However, the code rate is calculated according to $R = k/n = 1/3$.
From the lower diagram one recognizes that because of $d_{\rm min} = 3$ now also one bit error can be corrected.
During decoding, all light green points (with black outline) are transferred to the green point $(0, 0, 0)$ and all light blue points are transferred to the blue point $(1, 1, 1)$.
Up to two bit errors can be detected at the same time (one of course).

	The assignment $\underline{u} = (u_{1},\ u_{2},\ u_{3})$ → $\underline{x} = (x_{1},\ x_{2},\ x_{3})$ holds.
	The identity $\underline{x} = \underline{u}$ holds.
	The code rate is $R = 1$.
	The minimum distance between two code words is $d_{\rm min} = 2$.

	The code rate is $R = 1/4$.
	The code rate is $R = 1/3$.
	A bit error can be detected.
	A bit error can be corrected.

	Code $\mathcal{C}_{1} = \{(0, 0, 0),\ (0, 1, 1),\ (1, 0, 1),\ (1, 1, 0)\}$ is possible.
	Code $\mathcal{C}_{2} = \{(0, 0, 1),\ (0, 1, 0),\ (1, 0, 0),\ (1, 1, 1)\}$ is possible.
	Code $\mathcal{C}_{3} = \{(0, 0, 0),\ (0, 1, 1),\ (1, 0, 0),\ (1, 1, 1)\}$ is possible.